用Java Swing动画一步一步解释A*寻路算法

本文链接：https://blog.csdn.net/ximen502/article/details/138145082

内容来自RyiSnow视频讲解

Step by Step Explanation of A* Algorithm in Java

前言

这里作者在讲到2D历险记动作角色扮演游戏的时候，为了实现怪物或NPC跟踪玩家的功能使用到的算法。

这个视频是一个单独的讲解。最终效果，实现了玩家走到哪里怪物和NPC就跟到哪里。

作者用Java Swing可视化的方式详细讲解了A*寻路的实现过程。

效果

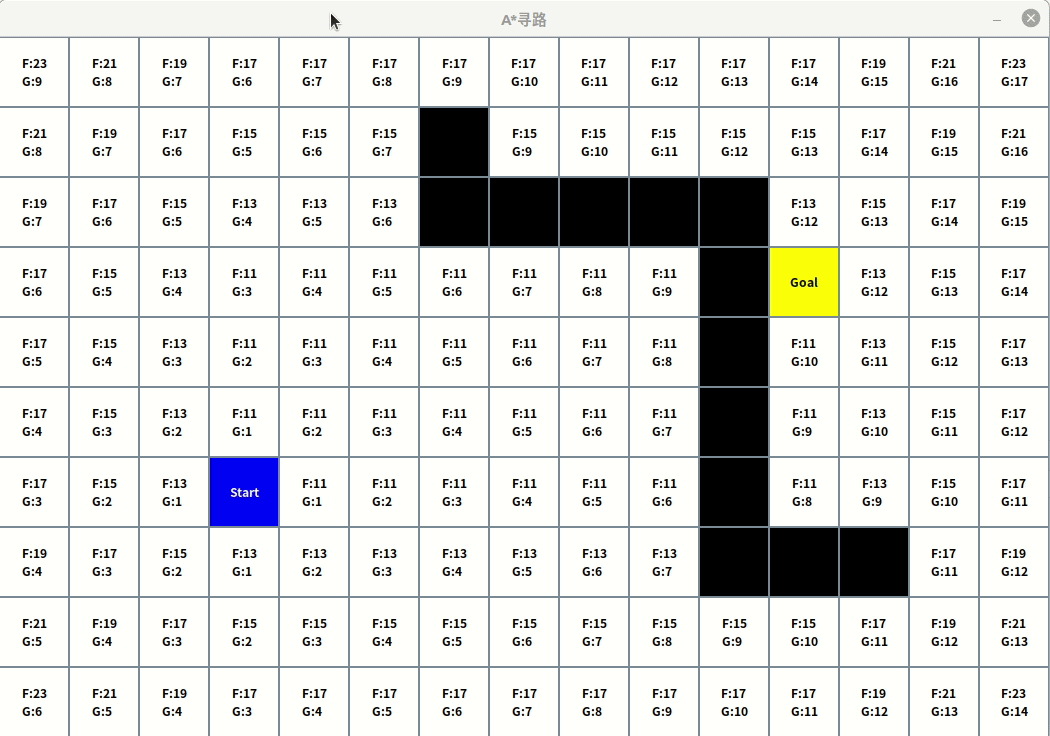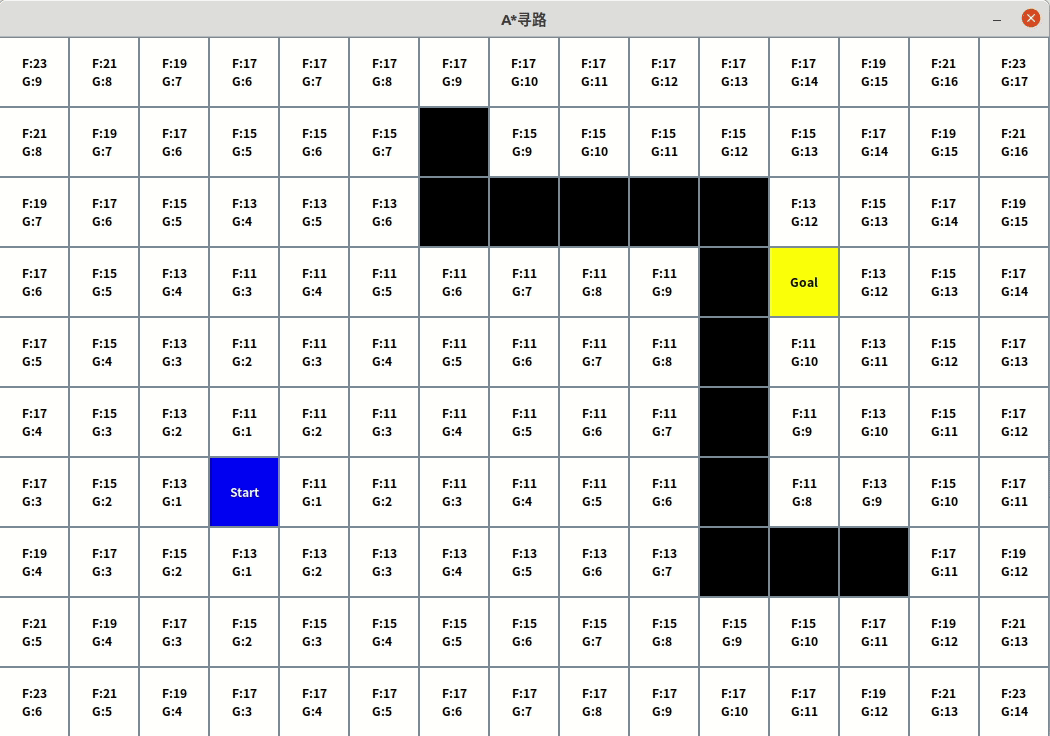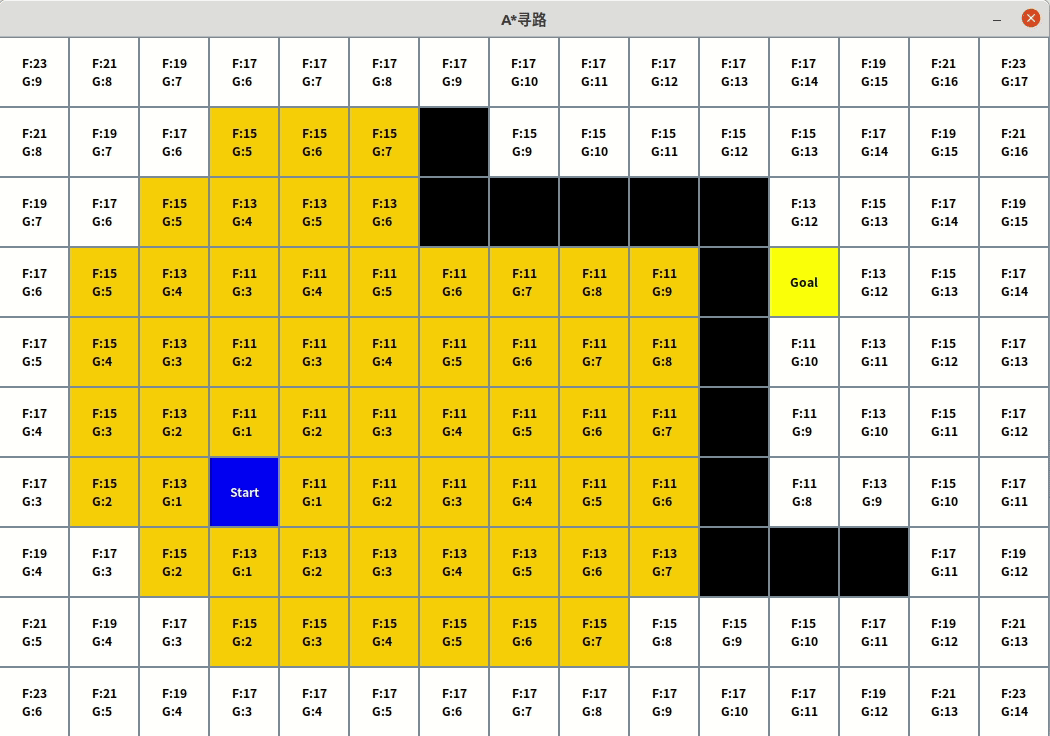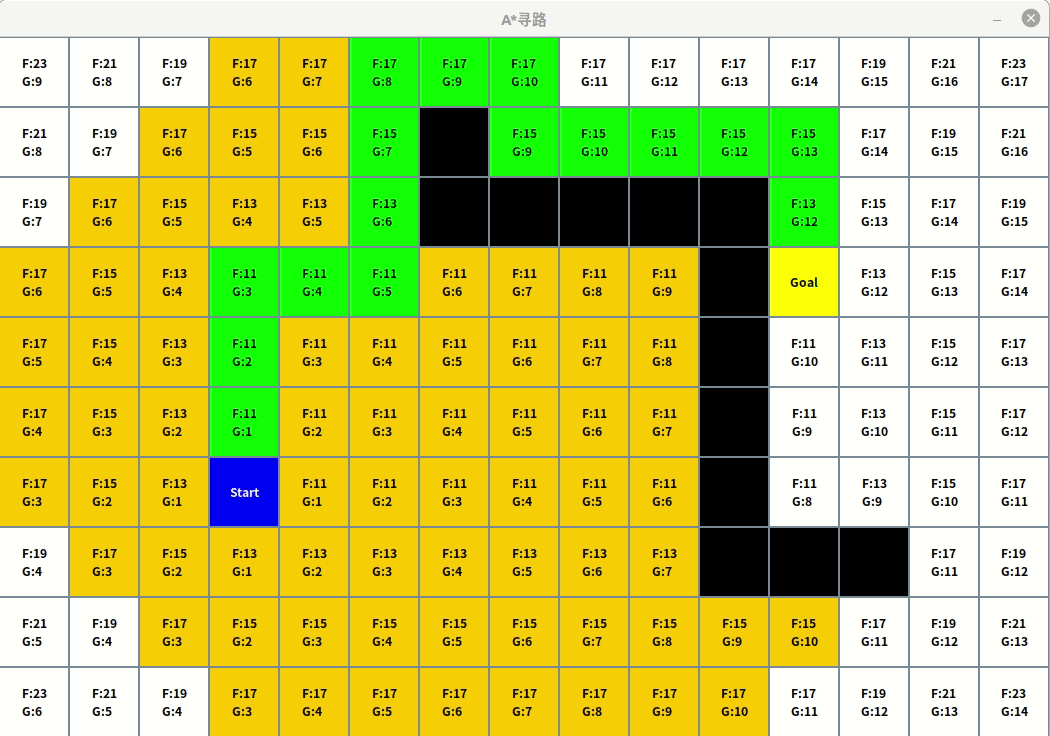
在这里插入图片描述

应用场景

在RPG游戏中，经常会有，玩家在地图点击一个点，让人物角色自动走过去的需求，或者怪物跟踪玩家，或者让NPC跟随自己。这些都是比较常见的应用场景。

起点和目标点或许有障碍物阻挡，有走来走去的某种角色阻挡。所以有人实现了一个算法，这样角色就可以自动计算最佳路径，总是能够适应屏幕上的情况，而不会卡在一个障碍物哪里过不去。

A*算法很好的实现了这个目的，被认为是最流行寻路算法之一。

具体过程

公式

$f (n) = g (n) + h (n)$

这里有三个点，起点、当前点、目标点，(start, current, goal)其中g(n)代表当前点与起点的距离，h(n)代表当前点与目标点的距离，f(n)代表两者之和。开始的时候起点也是当前点。

(这里以距离为例，实际情况可能是时间或金钱花费)

在这里插入图片描述

如果每个格子都是开放的，都可通过，他们之间也没有障碍物的话，找到最佳路径是容易的。

在这里插入图片描述
我们在2个点之间增加障碍物。

现在讨论一下A*寻路算法的实现机制。

为了评估最佳或最短路径， A*算法使用3个数字，他们分别被称为G cost(花费), H cost, F cost。

G cost当前点与起点之间的距离，这里的距离是两点之间的格子数。当前点一般在游戏中表示角色所在位置。

H cost当前点与目标点之间的距离。

F cost为G, F两者之和。
在这里插入图片描述

代码

示例代码中定义了一个Node类，其中包含三个变量gCost, hCost, fCost ，分别表示对应的花费，算法评估这三个花费，用于找出哪个节点是抵达目标节点最有希望的节点。

这三个花费里面，F花费是最重要的一个，因为它代表了总的花费。

计算每个Node节点的G，H，F

private void getCost(Node node) {
    // GET G COST (The distance from the start node)
    int xDistance = Math.abs(node.col - startNode.col);
    int yDistance = Math.abs(node.row - startNode.row);
    node.gCost = xDistance + yDistance;

    // Get H Cost (The distance from the goal node)
    xDistance = Math.abs(node.col - goalNode.col);
    yDistance = Math.abs(node.row - goalNode.row);
    node.hCost = xDistance + yDistance;

    // Get F cost (The total cost)
    node.fCost = node.gCost + node.hCost;

    // Display the cost on node
    if (node != startNode && node != goalNode) {
        String text = "<html>F:" + node.fCost + "<br>G:" + node.gCost + "</html>";
        node.setText(text);
    }
}

这里以两点之间的格子数作为距离。横纵坐标之和即两点间总的距离。这样G,H,F就都算出来了，接下来把他们显示在页面上。这里作者有意不显示H，如果有需要可以自己加上。

在这里插入图片描述

算法执行过程

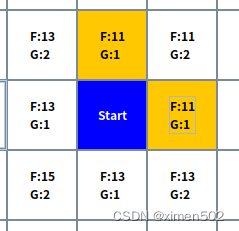
假设起点位置是玩家或NPC或其他任意角色，假设四个方向，上下左右都可以行走，在上图，先看相邻节点F cost，起点Start上下左右，左边、下边节点F为13，上边、右边节点F为11，显然上、右节点更有希望是距离最短路线上的点，再看G cost，两个节点G cost都是1，那么这两个节点就被选中。

继续以他们作为当前节点，继续向后评估F,G，选择节点。
在这里插入图片描述
在代码中search方法负责，将当前start起点的四个方向节点添加到一个ArrayList列表中，并将当前节点作为他们的父节点，方便回溯找路线，然后定义2个变量分别代表最佳节点索引bestNodeIndex=0，最佳节点fCost花费初始值bestNodefCost假设为999。（999需要根据实际情况来，不一定要用999）。

然后遍历这个ArrayList，根据fCost比较找到fCost更小的节点，如果fCost相等，则比较gCost，这时以gCost最小的节点为最有希望的节点。相应的修改bestNodeIndex与bestNodefCost。记录当前节点currentNode为找到的最有希望的节点，判断是否是目标节点，是的话，查找就不再执行了。

如果当前节点不是目标节点，在下一次查找中就会从ArrayList中移除掉currentNode，根据fCost和gCost继续遍历查找节点。直到找到目标节点。

代码

public void search() {
    if (!goalReached) {
        int col = currentNode.col;
        int row = currentNode.row;

        currentNode.setAsChecked();
        checkedList.add(currentNode);
        openList.remove(currentNode);

        // open the up node
        if (row - 1 >= 0) {
            openNode(node[col][row - 1]);
        }
        // open the left node
        if (col - 1 >= 0) {
            openNode(node[col-1][row]);
        }
        // open the down node
        if (row + 1 < maxRow) {
            openNode(node[col][row+1]);
        }
        // open the right node
        if (col + 1 < maxCol) {
            openNode(node[col+1][row]);
        }

        // Find the best node
        int bestNodeIndex = 0;
        int bestNodefCost = 999;

        for (int i = 0; i < openList.size(); i++) {

            //Check if this node's F cost is better
            if (openList.get(i).fCost < bestNodefCost) {
                bestNodefCost = openList.get(i).fCost;
                bestNodeIndex = i;
            }
            //If F cost is equal , check the G cost
            else if (openList.get(i).fCost == bestNodefCost) {
                if (openList.get(i).gCost < openList.get(bestNodeIndex).gCost) {
                    bestNodeIndex = i;
                }
            }
        }

        // After the loop, we get the best node which is out next step
        currentNode = openList.get(bestNodeIndex);

        if (currentNode == goalNode) {
            goalReached = true;
        }
    }
}

private void openNode(Node node) {
    if (!node.open && !node.checked && !node.solid) {

        // If the node is not opened yet, add it to the open list
        node.setAsOpen();
        node.parent = currentNode;
        openList.add(node);
    }
}

Track the nodes back and draw the path沿着节点原路返回，画出最短路径。

private void trackThePath() {
        
// Backtrack and draw the best path
    Node current = goalNode;

    while (current != startNode) {
        current = current.parent;

        if (current != startNode) {
            current.setAsPath();
        }
    }
}