故障电弧融合特征算法

1. 实现思想

故障电弧的产生具有很大的随机性且电弧阻抗为非线性，通过某一个特征量来判定故障电弧的方法准确率较低。基于此，这里采用了多特征量进行故障电弧综合评判。

通过阅读文献及对电弧电流的实验数据分析发现，电弧产生是线路运行状态中的突变现象，且随之电流波形也发生突变。因此把突变理论引入到故障电弧的检测中，首先提取多个表征电弧电流突变的特征量，其次运用突变理论指标评价的方法对特征量综合运算求出线路电流的突变隶属度值，作为故障电弧评价指标。

这里采用的特征量有：时域积分值特征、差值-均方根特征、高频脉冲特征、小波细节积分特征。

2. 名词解析

隶属度：若对论域（研究的范围）U中的任一元素x，都有一个数A（x）∈[0，1]与之对应，则称A为U上的模糊集，A（x）称为x对A的隶属度。

3. 故障电弧的一般特征

通过对故障电弧的实验测试，对电弧电流波形进行了分析，典型的线性负载和非线性负载电流波形如下图所示：

观察以上两种负载下的电流波形可以得出串联电弧有以下特征：

1. 电流峰值一般变小，偶尔也会变大。
2. 线性负载电弧电流出现零休现象，电脑负载正常电流也存在零休现象， 电弧产生时零休时间变长。
3. 波形畸变，出现半波缺失现象及正负半轴不对称。
4. 含有大量高次谐波。串联电弧的性质因负载不同而不同，研究发现并联电弧比串联电弧更容易发现，它的电压和电流特性更具有一般性。

4. 测试平台

主控芯片：NXP-RT1052

采样频率：10KHz

采样长度：256点

测试负载：1600w吹风机、350w手电钻、13*36w日光灯

5. 故障电弧特征分析

5.1 积分值特征提取

电弧故障时，电流幅值相比正常电流会发生变化，可能变大也可能变小。且所有负载的电流在电弧故障时都出现平肩部，或者平肩部时间变长，因而导致电流的周期积分值变小，因此可提取电流周期积分值进行分析。

其中，i(n)k 是第n 个周期第k 个采样点的电流值，k 为一个周期总采样点数。

为了为了衡量一个周期电流波形积分值的变化，这里引入了概念积分值变化系数，描述相邻周期积分值的变化率，该运算克服了由于负载功率不同造成的电流大小量级的不同的缺陷，公式定义如下：

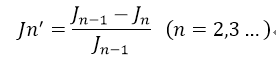
其中，Jn-1 为上一周期的积分值，Jn 为当前周期的积分值。

下面针对不同负载的积分值变化系数的测试结果如下：

图 5-1 吹风机积分变化率

 

图 5-2 手电钻积分变化率

 

图 5-3 日光灯积分变化率

 通过以上的数据分析可知，不同负载在产生电弧时，积分变化率相对于负载正常工作时，均有明显的增大现象。

5.2 差值-均方根特征提取

当负载正常运行时，电流波形为规则的周期波，电弧发生时电流波形发生畸变，出现不规律现象，如某些周期会出现半波，正负半轴不对称等，这种变化可通过差值-均方根法进行判别。首先运用公式(5-1)求得相邻周期电流相对应采样点的差值，再利用公式(5-2)求得相邻周期均方根值。

式中，i(n)k 为第n个周期第k个点的数值，i(n-1)k 为第n-1个周期第k个点的数值。

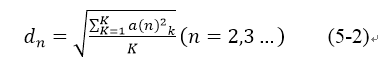
式中，dn 为相邻周期均方根，K为一个周期总采样点数。

为了克服不同负载电流大小量级的不同，还需要进一步计算。均方根的大小受相邻周期波形畸变大小影响，还受电流幅值的制约，因此这里运用公式(5-3)对不同负载的相邻周期均方根进行量化。 

 

式中，d'n 为量化后的相邻周期均方根，An-1 表示第n-1个周期的电流幅值，这里运用FFT计算基波电流幅值，能够有效地避免零漂引入的误差。

下面针对不同负载的差值-均方根的测试结果如下：