神经网络基础之激活函数

深度学习有两个非常重要的特性——多层和非线性

• 线性模型的局限性：只通过线性变换，任意层的全连接神经网络（Neural Network， NN）和单层NN模型的表达能力没有任何区别，而且它们都是线性模型。但是线性模型能解决的问题有限。
• 未使用激活函数时，每一层输出都是上层输入的线性函数，无论NN有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机了。

一、激活函数

1、含义

• 激活函数：指如何把“激活的神经元的特征”通过函数把特征保留并映射出来（保留特征，去除一些数据中是的冗余），这是NN能解决非线性问题的关键。
  
  • 激活函数是用来加入非线性因素的，因为线性模型的表达力不够。
  • （针对Relu的）构建稀疏矩阵（0较多），也就是稀疏性，这个特性可以去除数据中的冗余，最大可能保留数据的特征。
    
    • 激活函数的作用：能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。

2、性质

• 一般激活函数有如下一些性质：
• 非线性： 当激活函数是线性的，一个两层的神经网络就可以基本上逼近所有的函数。但如果激活函数是恒等激活函数的时候，即f(x)=x，就不满足这个性质，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的；
• 可微性： 当优化方法是基于梯度的时候，就体现了该性质；
• 单调性： 当激活函数是单调的时候，单层网络能够保证是凸函数；
• 输出值的范围： 当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的Learning Rate。

二、常见的非线性激活函数

• 常见的激活函数有 sigmoid 、 tanh、 relu 和 softplus 这4种。前两个最常用。

1、sigmoid函数

公式和图形：$S(x) = \dfrac{1}{1 + e^{-x}}$

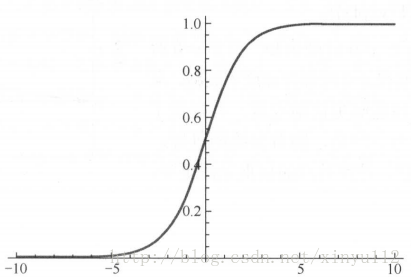
- 使用方法：tf.nn.sigmoid(features, name = None)

a = tf.constant([[1.0, 2.0], [1.0, 2.0], [1.0, 2.0]])
sess = tf.Session()
print(sess.run(tf.sigmoid(a)))
# 输出：[[ 0.7310586  0.88079703]
#             [ 0.7310586  0.88079703]
#             [ 0.7310586  0.88079703]]

• sigmoid函数的优缺点：
  
  • 优点：它的输出映射在（0, 1）内，单调连续，非常适合用作输出层，井且求导比较容易。
  • 缺点：由于其软饱和性，一旦输入落入饱和区，${f^{'}}(x)$就会变得接近于0，很容易产生梯度消失。

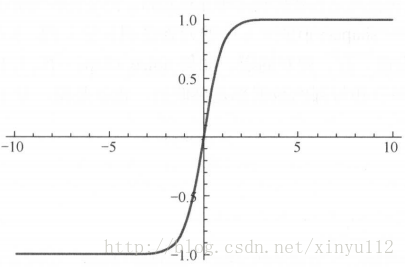
2、tanh函数

公式和图形：$S(x) = \dfrac{1 - e^{-2x}}{1 + e^{-2x}}$

• 使用方法：tf.nn.tanh(features, name = None)
• 特点：
  
  • 具有软饱和性
  • 由于其输出以0位中心，收敛速度比sigmoid要快
  • 仍无法解决梯度消失的问题
    

    饱和是指激活函数h(x)在取值趋于无穷大时，它的一阶导数趋于0。硬饱和是指当|x|>c时，其中c为常数，

    $$f'(x)=0$$ 。relu就是一类左侧硬饱和激活函数。

梯度消失是指在更新模型参数时采用 链式求导法则反向求导，越往前梯度越小。最终的结果是到达一定深度后梯度对模型的更新就没有任何贡献了 。

3、relu函数

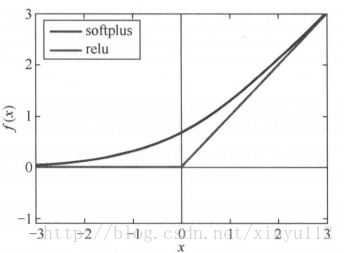
• 目前最受欢迎的激活函数。softplus可以看作是 ReLU 的平滑版本。
  
  • relu 定义为$f(x)= max(x,0)$。（下）
  • softplus 定义为$f(x)=log(l + exp(x))$。（上）
    
  • 使用方法：
  • tf.nn.relu(features, name = None)
  • tf.nn.relu6(features, name = None)
  • 如图所示：
  • relu在 x<0 时硬饱和。
  • x>0时导数为1，rule能够在x>0时保持梯度不衰减，从而缓解梯度消失问题，还能够更快地收敛，并提供了神经网络的稀疏表达能力。
  • 缺点：随着训练的进行，部分输入会落到硬饱和区，导致对应的权重无法更新，称为“神经元死亡”。

a = tf.constant([-1.0, 2.0])
with tf.Session() as sess:
    b = tf.nn.relu(a)
    print(sess.run(b))
# 输出：[ 0.  2.]

除了relu 本身外，TensorFlow 还定义了relu6，也就是定义在min(max(features, 0), 6)的tf.nn.relu6(features, name=None)，以及 crelu ，即tf.nn.crelu(features, name=None)。

4、dropout函数

• 一个神经元将以概率keep_prob决定是否被抑制。
  
  • 若被抑制，该神经元的输出就为0
  • 若不被抑制，该神经元的输出值将被放大到原来的 1/keep_prob 倍
• 在默认情况下，每个神经元是否被抑制是相互独立的。但是否被抑制也可以通过 noise_shape 来调节。
  
  • 当 noise_shape[i] == shape(x)[i］时， x 中的元素是相互独立的。
  • 若shape(x) = [k, l, m, n],x中的维度的顺序分别为批、行、列和通道
  • 若noise_shape = [k, l, l, n]，那么每个批和通道都是相互独立的，但是每行和每列的数据都是关联的（即要不都为0， 要不都还是原来的值）。
• 使用方法：tf.nn.dropout(x, keep_prob, noise_shape = None, seed = None, name = None)
  
  • x: 一个Tensor。
  • keep_prob: 一个 Python 的 float 类型。是否被抑制。
  • noise_shape: 一个一维的Tensor，数据类型是int32。代表元素是否独立的标志。
  • seed: 一个Python的整数类型。设置随机种子。
  • name: （可选）为这个操作取一个名字。

a = tf.constant([[-1.0, 2.0, 3.0, 4.0]])
with tf.Session() as sess:
    b = tf.nn.dropout(a, 0.5, noise_shape=[1, 4])
    print(sess.run(b))
    b = tf.nn.dropout(a, 0.5, noise_shape=[1, 1])
    print(sess.run(b))
# 输出：[[-0.  4.  0.  0.]]
#      [[-0.  0.  0.  0.]]

5、激活函数的选择

• 当输入数据特征相差明显时，用tanh的效果会很好，且在循环过程中会不断扩大特征效果并显示出来。
• 当特征相差不明显时，sigmoid效果比较好。
• 用sigmoid和 tanh作为激活函数时，需要对输入进行规范化，否则激活后的值全部都进入平坦区，隐层的输出会全部趋同，丧失原有的特征表达。而 relu 会好很多，有时可以不需要输入规范化来避免上述情况。
• 现在大部分的卷积神经网络都采用relu 作为激活函数。估计大概有 85%～90%的神经网络会采用 ReLU, 10%～ 15%的神经网络会采用 tanh，尤其用在自然语言处理上。

6、为什么要引入 ReLU 而不是其他的非线性函数（例如 Sigmoid 函数）？

• 采用 sigmoid 等函数，激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
• 对于深层网络，sigmoid 函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。
• Relu 会使一部分神经元的输出为 0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。