概率论的学习和整理--番外5：等差数列求和公式，等比数列求和公式，以及比较数列，函数，级数等相似概念

奔跑的犀牛先生

已于 2023-03-23 15:42:33 修改

阅读量3.7k

点赞数

分类专栏：概率和统计文章标签：概率论

于 2022-08-08 21:36:01 首次发布

本文链接：https://blog.csdn.net/xuemanqianshan/article/details/126236521

版权

概率和统计专栏收录该内容

40 篇文章

订阅专栏

等差数列：算术数列，arithmetic sequence，算术级数，中项是算术平均数
等比数列：几何数列， geometric sequence, 几何级数，中项是几何平均数

1 数列

1.1 什么是数列

数列：sequence of number
元素必须是数字
array1=1，2，3，4，5，6
数列就是数组，多个数存储在一起，数列名代表了这些所有数组里的所有数
可见数列也是函数，数列名就是函数名？

数列举例

array1=1，2，3，4，5，6
斐波拉契数列=1，2，3，5，8，13...
三角形数（点阵）=1，3，6，10，15
正方形数（点阵）=1，4，9，16

1.2 数列和各种概念比较

数列：一组数，一般是一维的
数组：多个同类型数据的集合（指代 / 容器）
一维数组就是数列，二维数组就是矩阵

和数学里不一样，编程里每个语言对这些的定义都不同

比如，一般编程语言里，数组必须存储相同类型的数据
但是python是动态语言
python里数组list，可以是一组数，甚至是不同数据类型的一组数据
python里的元组tuple，生成后不可改变
python里的字典，不允许重复

1.3 数列分类

按数列项数多少分：有穷数列，无穷数列

按数列大小变化规律分：递增数列，递减数列，摇摆数列
按数列变化规律分：周期数列
按数列项数多少分：等差数列，等比数列，等和数列

按数列项数性质分：常数数列

1.4 数列的解析表达

如果数列有规律，那就可能可以用函数表示
一般有规律的数列的表达式可以为

通项公式
递推公式

2 等差数列 Arithmetic Progression / arithmetic sequence

2.1 等差数列

等差数列 Arithmetic Progression
公差 d （common difference），公差通常用字母d表示
通项公式：
An = A1+ (n-1) *d
An=Sn-Sn-1, 特殊A1=S1
任意两项Am，An的关系为：An=Am+(n-m)d，等差数列广义的通项公式。

2.2 通项公式变形

An = A1+ (n-1) *d
An = A1+ n*d -1*d
An = n*d + (A1-1*d )
An= k*n+b
类一元一次函数

2.3 等差数列的求和公式 (等差数列的级数公式)

等差数列的前n项和等于首末两项的和与项数乘积的一半
a1+an=a2+an-1=a3+an-2=…=ak+an-k+1，k∈N*
隐藏Sn=n/2* (A1+An)

3 等比数列 Geometric Progression / geometric sequence

3.1 等比数列

等比数列 Geometric Progression
公比 r（common ratio）
通项公式：An=A1*Q^(n-1)
通项公式：An=Sn-Sn-1 ,n>=2

3.2 等比数列的性质

在等比数列中，依次每 k项之和仍成等比数列。
等比中项：q、r、p成等比数列，则 r 则为 q ，p的等比中项。
在等比数列中，首项与公比q都不为零。

其实，射影定理，也是等比数列的应用吧

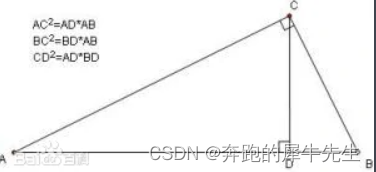
3.3 等比数列的求和（等比数列的级数）

等比数列的求和（等比数列的级数）

如果公比大于1，无穷情况下，是不收敛的，趋近于0的
如果公比小于1，无穷情况下，是收敛的，趋近于a1*1/(1-r)
无论公比多少，不等于0，有限个数情况下的求和

3.4 等比数列和“几何(geo)关系”，可叫几何数列

等比数列，中间项是前后两项的几何平均数
A1*p, A1*p^2 A1*p^3
A1*p * A1*p^3 = A1^2*p^4 =(A1*p^2)^2
等比数列，可以叫几何数列
英文里
等差数列：算术数列，arithmetic sequence，算术级数，中项是算术平均数
等比数列：几何数列， geometric sequence, 几何级数，中项是几何平均数

3.4.1 推论

数字呈几何级数增长，其实就是数列呈现等比数列的特征
数字呈指数级增长，其实就是数列呈现 f(x)=a^x的指数级关系

3.5 等比数列的和

等比数列和的推导过程

4 函数 function()

4.1 函数的定义

数学定义：形如 y=f(x) 的为函数
f(x) 为函数，y指代这个函数
程序里，有输入有输出的可以认为为函数

4.2 函数一般都有3种表示方法

列表法
图形法
解析法（不一定有解析式/ 通项公式）

5 级数（级数就是数列的求和函数）

5.1 级数 series

级数是指将数列的项依次用加号连接起来的函数。
典型的级数有正项级数、交错级数、幂级数、傅里叶级数等。
级数首先是一个函数
是把一个数列里得元素用 + 加号连接起来形成得一个表达式，由于有= 变成了函数
级数是函数，有返回值，返回值就是这些元素求和得结果

5.2 级数的表达式

5.3 简单级数

等差数列的和，也可以称为级数吧
等比数列的和，也可以称为级数吧

比如平方和级数

5.4 复杂级数（以后学习...）

典型的级数有正项级数、交错级数、幂级数、傅里叶级数等。
幂级数，就是级数项之间是几次方的关系
数项级数