线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？-CSDN博客

本文链接：https://blog.csdn.net/xuemanqianshan/article/details/132390283

本文介绍了向量和矩阵的基本概念，包括向量的表示方法（代数和几何），以及矩阵作为向量组的特性，如加法、数乘和点乘的等价关系。重点讲解了矩阵中元素的位置如何影响结果，并揭示了矩阵本质上是旋转和缩放的工具。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.3 向量/矩阵的优秀表示方法：即向量空间内的有向线段

2 矩阵

2.1 矩阵就是多个列向量的集合/合并（& 而不是 +），矩阵就是多个列向量的一种简化书写方式？

2.2 矩阵的加法 =等价于= 向量的加法

2.3 矩阵的数乘 =等价于= 向量的数乘

2.4 矩阵的点乘 =等价于= 列向量（或者行向量）的点乘

3 矩阵的特点

3.1 矩阵里不同位置的元素，影响范围是指定的有规律的

0 参考的知识点和目录

1 向量

1.1 向量的概念

向量/数组：一组有序的数
对应概念
标量/数：一个数字，单个的数

1.2 向量如何表示

常规的代数表示方法

比如，这样的向量 [1,5] [1,2,3] [1,3,5,7,9]

一维的几何方法表示

一般的表示方法就是

代数表示方法，基本就是原样列举： [1,2,3] 和 [1,3,2]
几何表示，比如用坐标轴上的点，表示向量/数组中的多个数字元素。但是这好像没啥意义，只是简单的用一条线上的不同点，表示了这个离散的数组，而且在坐标轴上还看不出来次序呢。
比如下图，[1,2,3] 和 [1,3,2] 就不好区分

二维的坐标轴表示

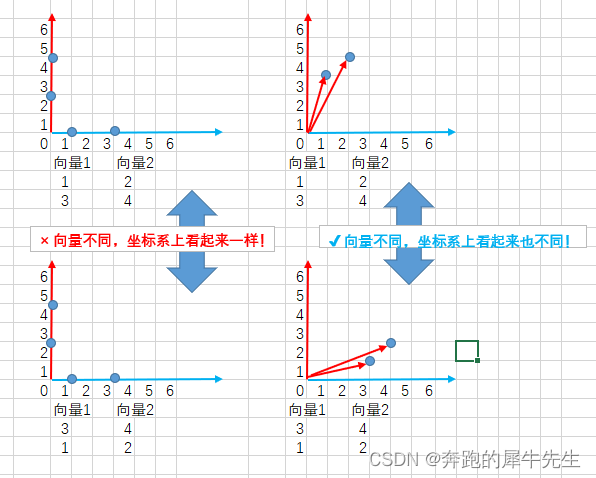
如果是2维的，比如是2个向量呢
用一根数量轴表示，全叠一起了，更不行把
比如表示1个2维向量 [1,3]
比如表示2个2维向量 [1,3] 和 [2,4]
比如表示2个2维向量 [3,1] 和 [4,2]

方式1：

如果把1个向量的全部元素全部标记在1个坐标轴上，不但有时候没法区分1个向量，有时候也无法区别2个向量。

方式2：

如果把1个向量的不同元素，映射为不同坐标轴上的点，那么向量本身就是成用多个坐标轴表示的一个有向线段。
这个有向线段，起点永远是原点，终点就是向量坐标（向量的元素）
只要向量的元素，或元素排序不同，最终向量的图形显示就会不同！
显然这个表示方法更好！

1.3 向量/矩阵的优秀表示方法：即向量空间内的有向线段

所以数学家们选的这个向量表示方法确实很巧妙，向量空间=张成空间

向量空间必须有原点
所有的向量都从原点出发
每个向量都是起点是原点，终点就是向量坐标（向量的元素）的一条有向线段
简化来看，终点（终点的坐标组）其实就可以代表向量了

2 矩阵=向量组

某些场合，列向量可以基本等价于行向量。乘法时不行。

矩阵就是多个列向量的集合
矩阵就是向量组
矩阵就是多个列向量的简要写法

矩阵完全可以拆分为多个列向量，只能用拆分为多个列向量的方法
反之，列向量可以合并为矩阵,只能用 and这种符号
因为矩阵 = 列向量1 & 列向量2 & ..... 按顺序从左到右合并的关系，而不是向量相加的关系

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} = \begin{bmatrix} a11 \\ a21 \end{bmatrix} and \begin{bmatrix} a12 \\ a22\end{bmatrix}$

但是只能用合并/and 来形容，而不能用加法来形如多向量合并为矩阵这个过程

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} = \begin{bmatrix} a11 \\ a21 \end{bmatrix} + (?) \begin{bmatrix} a12 \\ a22\end{bmatrix}$

矩阵 ≠ 列向量1 & 列向量2 & .....

矩阵 ≠ 列向量1+列向量2+ .....

2.1 矩阵就是多个列向量的集合/合并（& 而不是 +），矩阵就是多个列向量的一种简化书写方式？对，矩阵就是向量组

矩阵的列向量

矩阵的每一列向量都代表这个方向的基底ei 走到了对应列向量的位置。
比如这个矩阵 $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ ，它实际是 $\begin{bmatrix} 1 \\ 3 \end{bmatrix}$ 和 $\begin{bmatrix} 2 \\ 4 \end{bmatrix}$ 这2个列向量组成的。
第1个列向量 $\begin{bmatrix} 1 \\ 3 \end{bmatrix}$ 是第1个列向量对应的基 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ ，伸缩旋转到 $\begin{bmatrix} 1 \\ 3 \end{bmatrix}$ 的位置
第2个列向量 $\begin{bmatrix} 2\\ 4 \end{bmatrix}$ 是第2个列向量对应的基 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ ，伸缩旋转到 $\begin{bmatrix} 2 \\ 4 \end{bmatrix}$ 的位置

2.2 矩阵的加法 =等价于= 向量的加法

简化书写，浓缩书写

矩阵是把多个列向量写在一起的简化形式
也就是说以下是等价的：

如果把矩阵拆为多个列向量
矩阵相加，等于多个列向量分别相加后，再次合并为矩阵

2.3 矩阵的数乘 =等价于= 向量的数乘

如果把矩阵拆为多个列向量
矩阵标量乘法，等于多个列向量分别标量相乘后，再次合并为矩阵

2.4 矩阵的点乘 =等价于= 列向量（或者行向量）的点乘

矩阵的乘法，要特别注意，左乘和右乘
下面是AX=b的情况
需要把A拆为列向量
矩阵乘法和列向量乘法是等价的

下面是XA=b的情况
需要把A拆为行向量（反正要灵活一点）
矩阵乘法和这里拆的行向量乘法也是等价的

3 矩阵的特点

3.1 矩阵里不同位置的元素，影响范围是指定的有规律的

3.1.1 矩阵里数字的位置和影响范围

矩阵里的数字的位置
矩阵拆分为列向量

比如如果是 A*X=Y, x左乘矩阵A

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} * X=Y$

$\begin{bmatrix} a11 & a12 \\ a21 & a22\end{bmatrix} * \begin{bmatrix} b11 & b12 \\ b21 & b22\end{bmatrix} = \begin{bmatrix} a11*b11+a12*b21 & a11*b12+a12*b22 \\ a21*b11+a22*b21 & a21*b12+a22*b22\end{bmatrix}$

展开下

位置在a11的元素，会影响矩阵结果的，第1行第1个元素，第2个元素
位置在a12的元素，会影响矩阵结果的，第1行第1个元素，第2个元素
总结：第1行元素a11,a12 只会影响结果矩阵的第1行的内容
位置在a21的元素，会影响矩阵结果的，第2行第1个元素，第2个元素
位置在a22的元素，会影响矩阵结果的，第2行第1个元素，第2个元素
总结：第2行元素a11,a12 只会影响结果矩阵的第2行的内容

所以

总结：矩阵A第1行元素只会影响结果矩阵Y(或b)的第1行的内容
总结：矩阵A第2行元素只会影响结果矩阵Y(或b)的第2行的内容

$A*X=Y\rightarrow \begin{bmatrix} 2 & 0 \\ 0 & 3\end{bmatrix} *X=Y \rightarrow \begin{bmatrix} 2 & 0 \\ 0 & 3\end{bmatrix} *\begin{bmatrix} b11 & b12 \\ b21 & b22\end{bmatrix} =\begin{bmatrix} 2*b11 & 2*b12 \\ 3*b21 & 3*b22\end{bmatrix}$