[离散数学] 图论（图树欧拉图哈密顿图平面图及着色二部图）

Tumb1eweed

已于 2025-03-22 16:57:02 修改

阅读量1.9k

点赞数 54

分类专栏：离散数学文章标签：图论

于 2025-03-22 10:28:53 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/xueyanshang4089/article/details/146405413

版权

离散数学专栏收录该内容

4 篇文章

订阅专栏

图的基本概念

基本概念见教科书定义，图论概念很多

简单图和多重图

在这里插入图片描述

度最小度最大度最小出度最大出度

在这里插入图片描述

在这里插入图片描述

生成子图导出子图补图

在这里插入图片描述

子图：点不全边不全
生成子图：点全边不全
导出子图：点不全边不全，但只要出现的点，端点是出现的点集里的边必须全

补图：
在这里插入图片描述

在这里插入图片描述
千万要注意不要遗漏顶点，画的时候先把所有的点画上去，没有的边再补

完全图有向完全图竞赛图正则图

在这里插入图片描述
点的个数就是阶数

握手定理

在这里插入图片描述

图的同构

在这里插入图片描述
彼得森图：

通路与回路图的连通性

在这里插入图片描述

无向图的连通性

在这里插入图片描述

PS：用商集来定义连通分支还挺方便的

极小性是指如果不是删掉点割集里所有的点的话则无法达成前面的条件，点割集的所有点都需要删掉才能让连通图不连通，分支变多。

在这里插入图片描述

连通度相当于至少删掉几个节点（边）才不连通，有点像阶的概念
在这里插入图片描述
最后一个是图的最小度
点连通度 <= 边连通度 <= 图的最小度

有向图的连通性

在这里插入图片描述

图的矩阵表示

欧拉图哈密顿图最短路径

欧拉图

在这里插入图片描述

有没有简单的方式判定是否是欧拉图呢？
有的兄弟，有的：
无向欧拉图和半欧拉图
在这里插入图片描述

有向欧拉图和半欧拉图
在这里插入图片描述

在这里插入图片描述

哈密顿图

哈密顿图定义
在这里插入图片描述
最后一条很重要

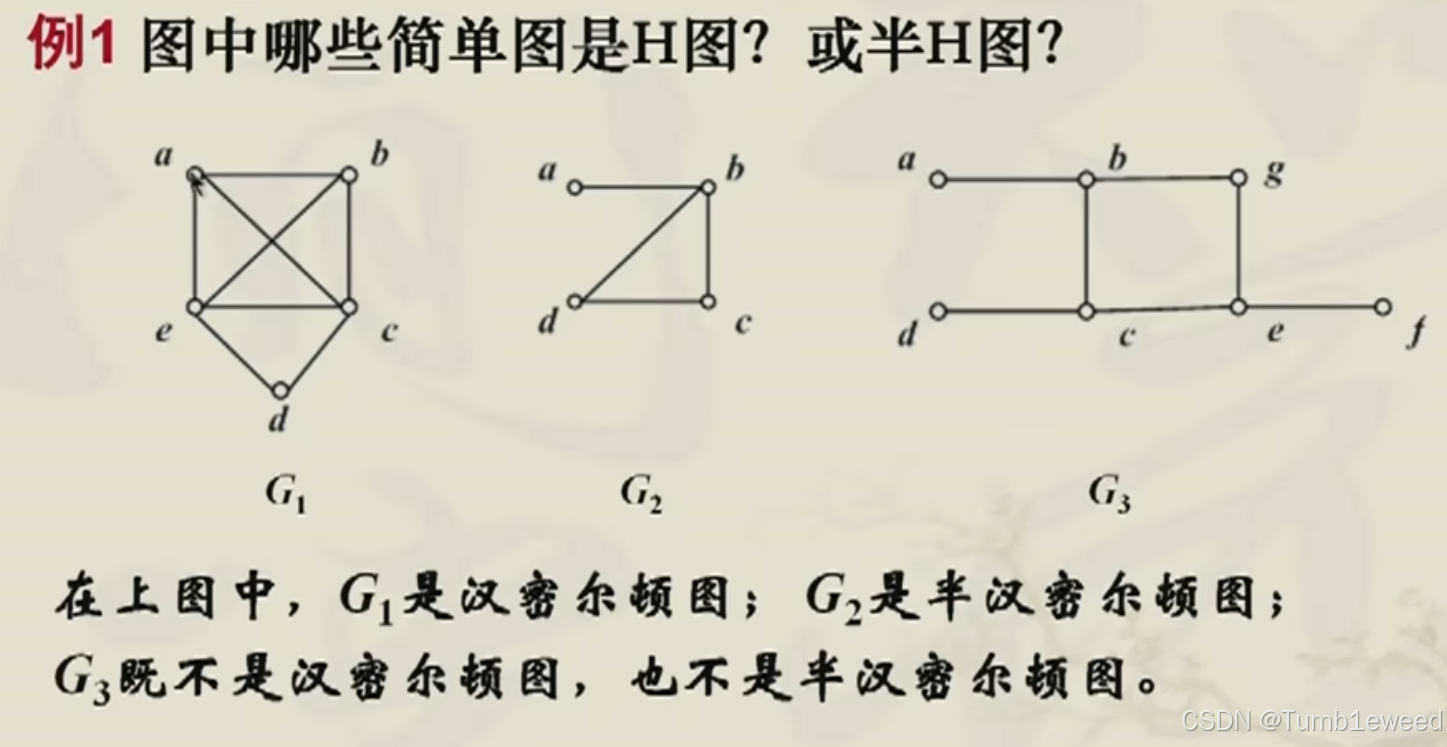
无向哈密顿图的必要条件

在这里插入图片描述
必要性用来判定不是，充分性用来判定是

有桥的图，删去桥的任意一个顶点就等于把桥删了，那么删掉一个点连通分支变成2，说明肯定不是哈密顿图。

无向哈密顿图的充分条件

在这里插入图片描述
这个定理好理解，两个度加起来>= n-1，说明这两个点中间必然关联着一个点，通过这个点可以把这两个点连通起来。

有向哈密顿图的充分条件

在这里插入图片描述
左边 $V_1...V_{r-1}V_{k+1}V_r$ ，右边左边 $V_{k+1}V_1...V_{r-1}V_{k}$

平面图对偶图图着色

平面图的定义：在这里插入图片描述

平面嵌入
在这里插入图片描述

注意当一条边没有分割开两个面，而是在一个面内部时，这条边在次数上要算两次，这也符合下面的定理：
在这里插入图片描述

欧拉公式以及推广

在这里插入图片描述
用归纳法可证明
下面是一系列推广定理：

平面图的判断

在这里插入图片描述

边的收缩

对偶图与着色

对偶图

平面图的区域着色可以转化为对偶图的点着色
在这里插入图片描述

对偶图相比原图，点数和面数互换了
对偶图点的度数=原平面图面的次数

自对偶图
在这里插入图片描述

点着色

在这里插入图片描述

图着色应用

在这里插入图片描述

二部图

在这里插入图片描述

简单来说就是二部图任何回路的长度都是偶数。

(1)(2)(3)是二部图，(4)不是

关键活动

略

树

无向树的定义

在这里插入图片描述
无向图的等价定义

在这里插入图片描述

生成树

在这里插入图片描述

在这里插入图片描述

基本回路系统基本割集系统
在这里插入图片描述

在这里插入图片描述

基本回路系统是由弦产生的回路，基本割集系统是由树枝产生的，删去树枝后连接两颗子树的边就是由该树枝产生的基本割集（包括该树枝）
在这里插入图片描述

最小生成树

在这里插入图片描述

根树

有向树

在这里插入图片描述
注意有向树是不考虑边的方向时是一棵树

子树

在这里插入图片描述

也可以看做，每个点（除根节点）上面都仅连着一条边，而这些边又都是有分支节点生成的。
或者可以从握手定理来证明

哈夫曼树

略

二叉树遍历

略

参考资料

《离散数学》第二版屈婉玲 —— 高等教育出版社
东北大学离散数学 MOOC

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。