本总结是是个人为防止遗忘而作,不得转载和商用。
前提说明:因为在做此总结之前我已总结过“感知机算法”,而这里的很多知识(包括预备知识)和“感知机算法”中有重叠,所以本总结的知识不会像我做的其他教程那样对每个知识点都做很详细的解释,如果你已经掌握了“感知机算法”的相关知识,那本总结对你是没问题的,反之,你就需要了解下“感知机算法”了。
回归问题
线性回归的一般形式如下:
其中x是已知的一个个样本点,θ是未知的权重。
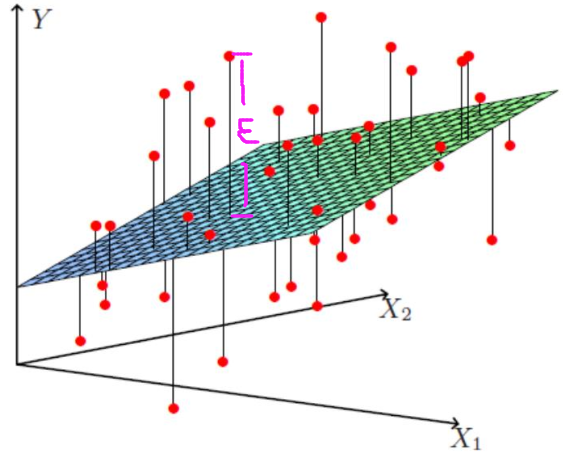
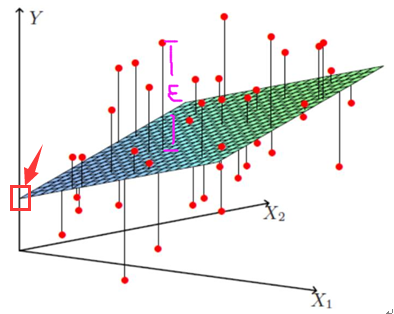
但如下图所示:
上图的每个红点是一个个样本点即x,上图的平面就是回归后的平面即hθ(x)。
一般情况下,我们不可能让hθ(x)完全拟合数据(那样就过拟合了),于是最终求得hθ(x)与的每个样本点的实际位置就有个差值(上图粉红色标注的那段距离),这就是残差。
一般用ε表示残差,于是hθ(x)就更新成:
hθ(x) =θTx +ε
残差ε是独立同分布的,因为若以卖房子为例子,那房子的价格的残差(这里残差就是指:房价不是正常定价,莫名其妙的高那么点或低那么点)一定是定房价的那个人/团队因为某种原因这么做的,而既然出自一个人/团队之手,那所有的残差一定符合这个人/团队的考虑吧,于是就属于这个人/团队的分布 -- 属于同一个分布,而每个房子和房子的残差是没关系的(隔壁房子就是精装修,那和你想买的房子有半毛钱关系?)-- 独立,所以残差是独立同分布。
不过这个残差到底是什么分布呢?
答案是:服从均指为0,方差为某个定值σ2的高斯分布。其理论依据是:中心极限定理。
如何求θ
下面的问题是如何求θ,步骤如下:
1,利用最小二乘法的知识写出θ的目标函数
PS:hθ(x(i))可以写成所有样本数据组成的矩阵X乘上样本权值θ的向量的形式,而如果hθ(x)写成了这样的形式,那y(i)也需要用一个向量y表达,第二个等号就是这样来的。
2,对J(θ)求梯度后令梯度=0来求驻点。
3,得到结果
θ= (XTX)-1XTy
PS:这个结果有个简单的记法(可以这样记,但一旦有人问这个结果的来历,可不能这样回答):Xθ= y => XTXθ= XTy => θ= (XTX)-1XTy
话说,有时为了防止过拟合和防止XTX不可逆(样本个数<维度)的情况,增加λ扰动
θ= (XTX+λI)-1XTy,I是单位阵
广义逆矩阵(伪逆)
一般若矩阵是方阵的话可以求其逆矩阵,如,若x是个方阵则:
xθ= y => θ= x-1y
但若x不是方阵,那上面的转换就不行了,这时就要用到伪逆了。
什么是伪逆?看上面“如何求θ”的结果,即对于:
xθ= y => θ= (xTx)-1xTy
这时(xTx)-1xT就起到了x-1的作用,因此就把(XTX)-1XT称作广义逆矩阵,简称伪逆,用x+表示。
总结一下:
若x为可逆方阵,(xTx)-1xT即为x-1,因为:
(xTx)-1xT= x-1(xT)-1xT = x-1
若A为矩阵(非方阵)时,称x+为x的广义逆矩阵(伪逆)。
线性回归的复杂度惩罚因子
话说,对于线性回归的目标函数
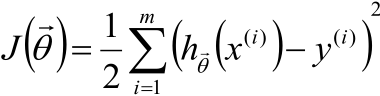
我们是不希望每个θ特别大,因为这样一来θiX(i)的值就会就会差距很大,这样对每个样本预测的结果hθ(x(i))就会波动的很厉害。因此,我们的目标还得多一个:让每个θ都尽可能的趋近于0,于是给目标函数增加θ的平方和损失成为了下面的形式:
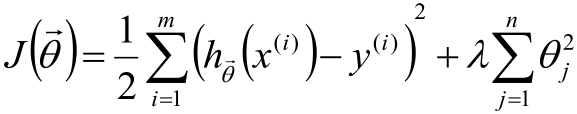
PS:这里假设θ服从高斯分布。
为了更有概念,这里还以房价预测举个例子:假设我们通过某种方式搜集到了“房屋大小、房屋朝向、小区环境、交通情况”等10W个特征,这时如果每个θ都不为0且很大的话,那这个模型是很庞大的,但可能有些特征对房价预测的影响度太小以至于可以忽略不计的话,那就让这些样本对应的θ= 0,这样一来这些特征就成功的被模型忽略了,从而达到对模型降维的目的!
最后在从新说一遍,式1是标准的损失函数,式2中多出来的那一块中除去λ的部分是为了让θ不要过大而加的一个正则项,既然加了正则项那就需要再加一个λ作为超参数来进行调节,而既然λ是超参,那就没法求(是不是从刚才起就在纳闷λ怎么求),只能通过别的方式给我们只能这样。
PS:这里超参的作用是:在式2这整个损失函数里,如果λ很大,则λ修饰的那一块占得比例就大,反之占得比例小。
那超参数λ应该如何取呢?答案是:事先给一个,你拍脑门也好按照经验也好直接给一个,话说机器学习里总是说调参调参,调的就是这个参。
| 说实话,关于超参我之前一直很疑惑,所以这里就在多啰嗦一点,用一个不太恰当的例子来说明它,希望能帮助你理解。 话说咱们写代码时经常说“要么时间换空间,要么空间换时间”,于是乎时间和空间分别占多少比例就值得我们推敲了,这里我用这么一个式子“最终效果 = 时间+λ空间”来表示两者关系是可以的吧,这里λ就是个超参数,它用来调节“时间”和“空间”对于最终效果的影响度,因为假设λ是个无限大的值,那对于最终效果来说,时间的影响度就可以忽略了,反之如果λ是个无限趋近于0的数,那空间就可以pass。而λ给多少这个根本没办法通过某种数学公式求,只能一开始先拍脑门随便给一个λ值或者按照经验给一个λ值,然后在一次次的实验中不断调节λ直到我们感觉达到最优。 |
因此在机器学习中,经常这样分类数据:
1,如果模型是这样:
那就如下图所示:
把整个数据集分成两部分,一部分用于训练参数θ,一部分用于测试效果。
2,如果模式是这样:
那就如下图所示:
从训练数据中本来用来训练参数θ那部分中预留一部分用于验证当前的超参数λ怎么样。
另:机器学习中有个“十折交叉验证”,感兴趣的可以自己去查查。
最后
还是之前如何求θ的公式:
θ= (XTX)-1XTy
话说这样求θ是没一点问题的,不过在机器学习中习惯使用梯度下降算法来求θ,这个我已经总结了,这里就不再写了。
线性回归的代码
这里data是一个类似下图这样的矩阵
1 x01 x02 ... x0n y0
1 x11 x12 ... x1n y1
...
1 xm1 xm2 ... xmn ym
其中,第一列是截距,如下图所示:
这里的1就是箭头所指的位置,注意:这个和残差不一样。
xij是样本的特征,每一行对应一个样本
ym是样本的结果。








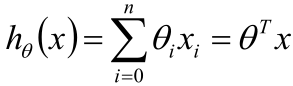
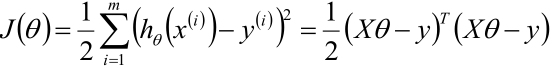
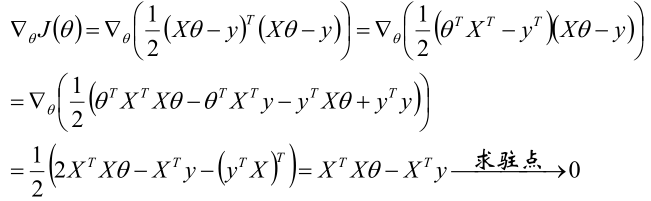
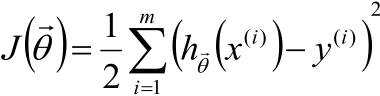


















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








