gradient descend/accelerated gradient descend/linearSVM/libSVM

% four methods:
%               gradient descend method
%               accelerated gradient method
%               linearSVM
%               libSVM

clear;clc;close all;
%% produce two class data
mu = [2 3];
SIGMA = [1 0; 0 2];
r = mvnrnd(mu,SIGMA,100);
plot(r(:,1),r(:,2),'r+');
hold on;
mu = [7 8];
SIGMA = [ 1 0; 0 2];
r2 = mvnrnd(mu,SIGMA,100);
plot(r2(:,1),r2(:,2),'*')

% train data
n = size(r,1)*2; % the number of train samples
m = size(r,2); % feature length
trainFeature = zeros(n,m);
trainDistribution  = zeros(n,1); % two classes
trainFeature(1:n/2,:) = r;
trainFeature(n/2+1:end,:) = r2;
trainDistribution(1:n/2) = -1; % neg samples
trainDistribution(n/2+1:end) = 1;% pos samples
train_num = n;
opt = struct;


% gradient descend : loss function : 1\n *sum (y-wTx)^2
opt.usedBias = 1; % if >= 0, use Bias,or not use Bias
[fval1,Wg] = grad_descend(trainDistribution,trainFeature,opt);

% accelerated gradient descend : loss function ： 1\n * sum(y-wTx)^2
opt.usedBias = 1;
[fval2,Wa] = acc_grad_descend(trainDistribution,trainFeature,opt);

% using linearSVM
% -B 1>=0 represent using bias
which train
lin_model = train(trainDistribution,sparse(trainFeature),'-s 1 -B 1');
result1 = predict(trainDistribution,sparse(trainFeature),lin_model);

% using libsvm
which svmtrain
lib_model = svmtrain(trainDistribution,trainFeature,'-t 0');
result2 = svmpredict(trainDistribution,trainFeature,lib_model);

% compute w
% w= \sum_i a_i*x_i*y_i
sv_vec = full(lib_model.SVs);
lib_model.w = sum(repmat(lib_model.sv_coef,1,2).*sv_vec,1)';

x1 = -2:0.1:10;
% wx+b=0;
% w1 * x1 + w2 * x2 + b = 0;
Wg_x2 = (-Wg(3)*ones(1,length(x1))-Wg(1)*x1)./Wg(2);
Wa_x2 = (-Wa(3)*ones(1,length(x1))-Wa(1)*x1)./Wa(2);
lin_x2 = (-lin_model.w(3)*ones(1,length(x1))-lin_model.w(1)*x1)./lin_model.w(2);
lib_x2 = (lib_model.rho*ones(1,length(x1))-lib_model.w(1)*x1)./lib_model.w(2);
% plot split line
plot(x1,Wg_x2,'b');
plot(x1,Wa_x2,'g');
plot(x1,lin_x2,'r');
plot(x1,lib_x2,'k');
legend('neg ','pos','gradient','accelerated','lineSVM','libSVM');
% y=wx+b ,if y>0 ,label = 1 ,else label = -1,b=-lib_model.rho
r=trainFeature*lib_model.w-lib_model.rho;

function [fval,W] = acc_grad_descend(trainDistribution,trainFeature,opt)
% accelerated gradient descend

if opt.usedBias >= 0
    t = zeros( size(trainFeature,1),size(trainFeature,2)+1);
    t(:,1:end-1) = trainFeature;
    t(:,end) = opt.usedBias;
    trainFeature = t;
end

err = 0.00001;
maxIter=10000;
beta=0.5;% bete \in (0,1)
gamma=1;

if opt.usedBias >=0
    W0 = zeros(3,1);
else
    W0 = zeros(2,1);% inital weights
end
V0 = W0;
i = 0;
t = 0;
a0 = 1;
while true
    % search a proper step size
    if i==maxIter
        exitFlag=' maxIter ';
        break;
    end
    while true
        grad = compute_grad(trainDistribution,trainFeature,V0);
        V = V0-gamma*grad;
        [fval,m_xk] = compute_fval(trainDistribution,trainFeature,V,V0,gamma,grad);
        if fval <= m_xk
            break;
        end
        gamma = gamma*beta;
    end

    W = V;
    a = 2/(t+3);
    delta = W-W0;
    V = W+(1-a0)/a0*a*delta;

    if norm(delta,2)<err
        exitFlag = ' achieve precise';
        break;
    end

    % save last time's data
    a0 = a;
    W0 = W;
    V0 = V;
    i  = i+1;

end

disp(exitFlag);
end

function [fval,m_xk] = compute_fval(trainDistribution,trainFeature,V,V0,gamma,grad)
train_num = size(trainFeature,1);
% f(x_{k+1})
fval = 1/train_num*sum(sum((trainDistribution-trainFeature*V).^2));

% m_{x_k,\gamma_k}(x_{k+1})
% m_xk=f(x_k)+<\triangledown f(x_k),x-x_k>+frac{1}{2\gamma_k} ||x - x_k ||^2
fval0 = 1/train_num*sum(sum((trainDistribution-trainFeature*V0).^2));

m_xk = fval0+grad'*(V-V0)+1/(2*gamma)*norm(V-V0,2)^2;
end

function grad = compute_grad(trainDistribution,trainFeature,W0)
train_num = size(trainFeature,1);
grad = -1/train_num*(2*trainFeature'*(trainDistribution-trainFeature*W0));
end


function  [fval,W]=grad_descend(trainDistribution,trainFeature,opt)
% the convergence rate of gradient descend is very slowly!

if opt.usedBias >= 0
    t = zeros( size(trainFeature,1),size(trainFeature,2)+1);
    t(:,1:end-1) = trainFeature;
    t(:,end) = opt.usedBias;
    trainFeature = t;
end

beta=0.5;% bete \in (0,1)
gamma=1;
maxIter = 10000;
err = 0.00001;
i = 0;

if opt.usedBias >= 0
    W0 = zeros(3,1);
else
    W0 = zeros(2,1);
end

while true
    if i==maxIter
        exitFlag = 'achieve max iter number';
        break;
    end
    %     rate = a0/(1+k*i);
    %     grad = -1/train_num*(2*trainFeature'*(trainDistribution-trainFeature*weights));
    %     weights = weights-rate*grad;
    %     fval = 1/train_num*sum(sum((trainDistribution-trainFeature*weights).^2));
    while true
        grad = compute_grad(trainDistribution,trainFeature,W0);
        W = W0-gamma*grad;
        [fval,m_xk] = compute_fval(trainDistribution,trainFeature,W,W0,gamma,grad);
        if fval <= m_xk
            break;
        end
        gamma = gamma*beta;
    end
    if norm(W-W0,2) < err
        exitFlag='achieve precise';
        break;
    end
    i = i+1;
    W0 = W;
    fprintf('%.6f \n',fval);
end
disp(exitFlag);
end

acc/grad 几乎重叠

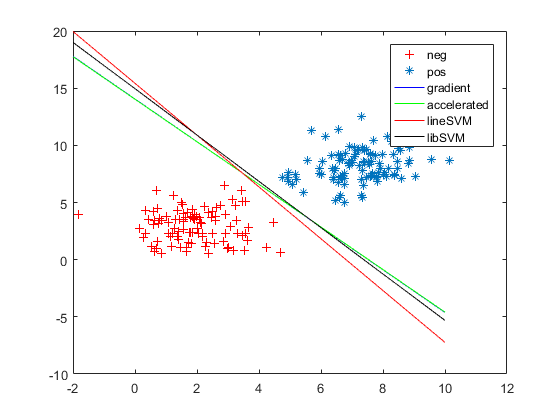
其他一些图,下图只给出grad,而没有画出acc：
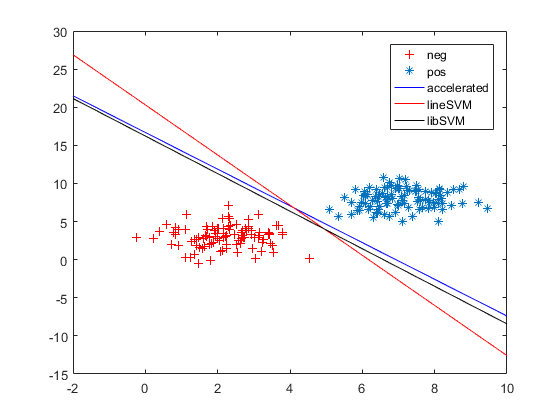
1.从这个图，给我们的感觉是grad/acc似乎得到了更好的效果。

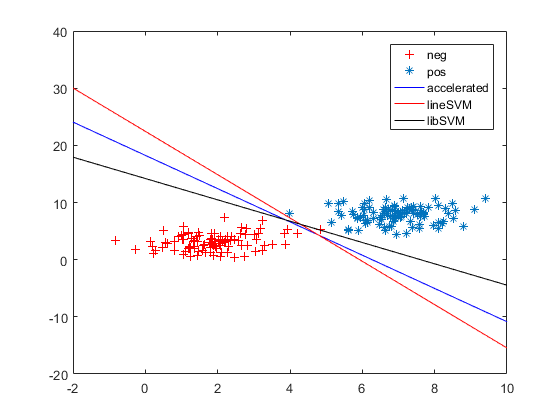
2. 从这个图，我们可以看出libsvm为了使训练样本全部分布正确，形成的超平面已经不是我们期望的那样，而grad/acc和linearsvm似乎更是我们想要的效果。

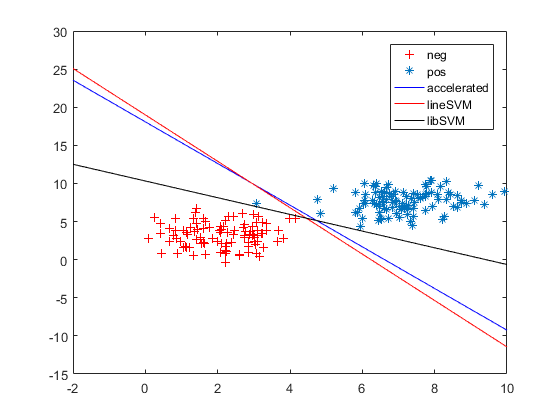
3.同图2，

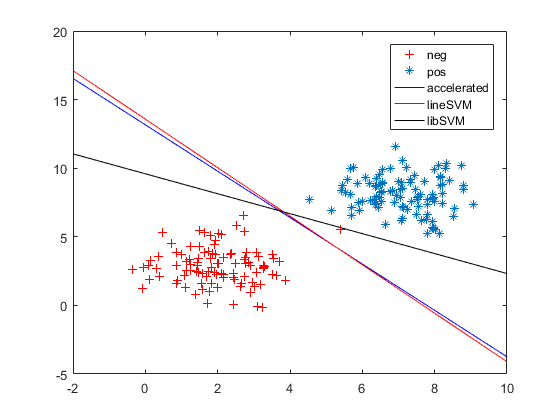
4. libsvm似乎达到了更好的效果。

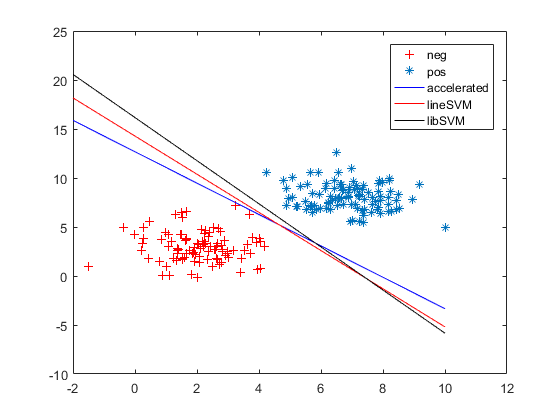
5. linearsvm似乎使我们想要的效果

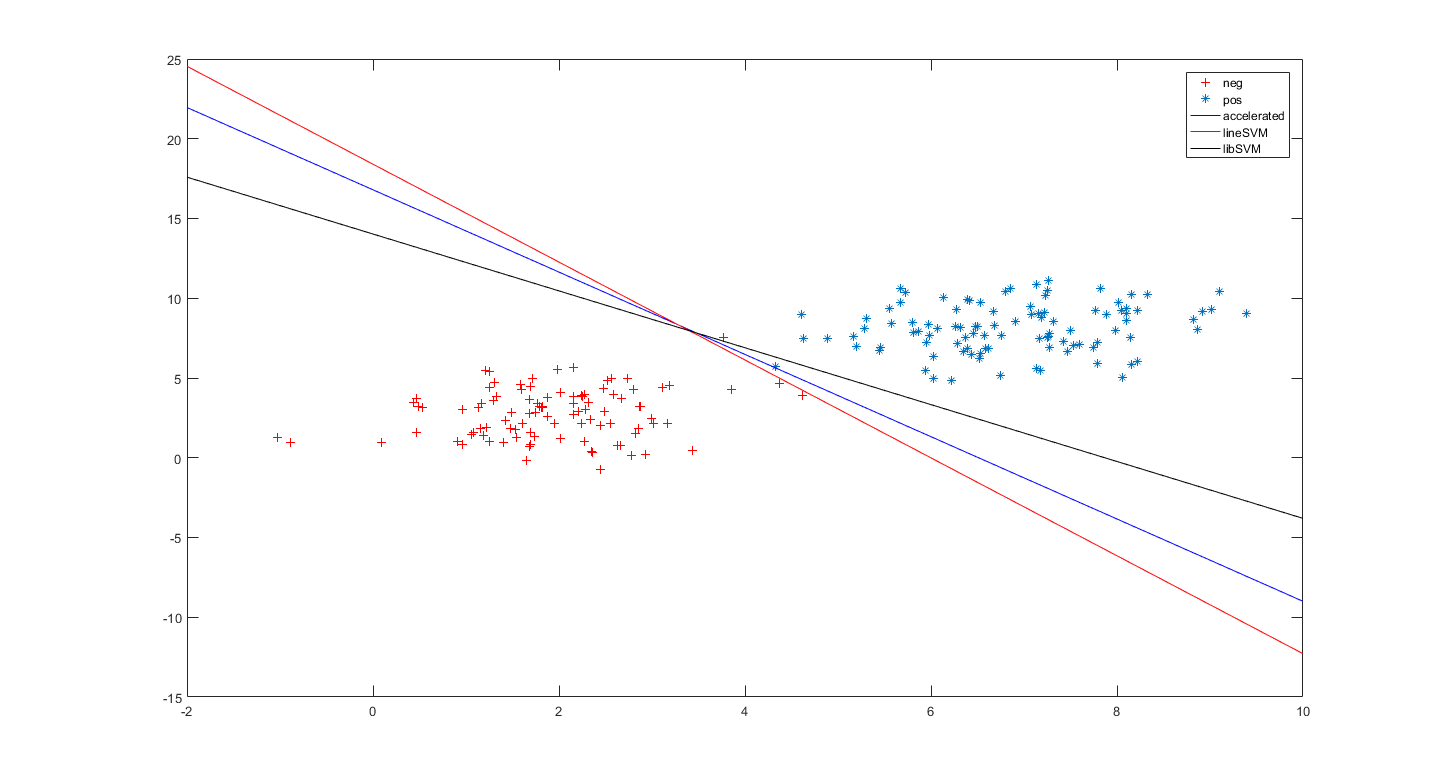
6. linearsvm和libsvm都有一定的容忍误差，grad/acc为了训练样本全部分类正确。

总结：
总的来说，linearsvm和libsvm都是学习一个超平面的思想。从这个概念上来讲其效果应该优于grad/acc。但是，不管linearsvm，libsvm ,还是grad/acc，如果从分类精度来衡量模型参数好坏的化，很难进行评判。只要我们稍微修改一下linearsvm,libsvm,grad/acc的训练参数就会得到不一样的结果。