概率论学习二、样本空间与事件

本文学习资源来自《概率论基本（李贤平）》

一、样本空间

为了研究随机试验，首先需要知道这个试验可能出现的结果。这些结果称为样本点，一般用$\omega$表示。样本点全体构成样本空间（sample space），用$\Omega$表示。

在概率论的研究中，一般都假定样本空间是给定的，这是必要的抽象，这种抽象使我们能更好地把握住随机现象的本质，而且得到的结果能广泛地应用。事实上，一个样本空间点的样本空间可以概括各种实际内容很不相同的问题。

二、事件

所谓给定一个点的集合$S$，是指对于任何一个点$\omega$，都可以确定它是不是属于$S$，如果是，则记为$\omega \in S$； 如果不是，则记为$\omega \notin S$。
按照这种定义，单个点也是一个点集。习惯上还约定不包含任何点的集合也是一个点集，称为空集，记为$\varnothing$

今后，我们把事件定义为样本点的某个集合，称某事件发生当且仅它所包含的某一个样本点出现。

因此，虽然试验的全部可能结果在试验前就很明确，但是只有到了试验之后，才能确定某一特定的事件是否发生。

我们把样本空间$\Omega$也作为一个事件，因为在每次试验中必然出现$\Omega$中的某个样本点，也即$\Omega$必然发生，所以常称$\Omega$为必然事件。类似地，我们把空集$\varnothing$也作为一个事件它在每次试验中都不会发生，称为不可能事件。

必然事件$\Omega$在试验中必然地发生，相反地，不可能事件在任何试验中不可能发生，必然事件与不可能中以说不是随机事件。但为了今后研究的方便，我们还是把必然事件与不可能事件作为随机事件的两个极端情形来统一处理。

三、 事件的运算

在一个样本空间中显然可以定义不止一个事件。概率论的重要研究课题之一是希望从简单事件的概率推算出复杂的事件的概率。

若$A$中的每一个样本点都包含在$B$中，则记为$A \subset B$或 $B \supset A$，并称$A$是$B$的特款，亦称事件$B$包含了事件$A$，这时事件$A$的发生必然导致事件$B$发生。

如：若以$A$记“来到呼叫不超过5个”，以$B$记“来到呼叫不超过6个”，则$A \subset B$。显然对任何事件$A$，必有$\Omega \supset A \supset \varnothing$

如果 $A \supset B$ 与 $B \supset A$同时成立，则称$A$与$B$等价，或称$A$等于$B$，记为$A=B$，等价的两个事件同时发生，因此可看作是一样的。

对于事件$A$，由所有包含在$A$中的样本点所组成的事件称为$A$的逆事件，或称$A$的对立事件，记为$\overline A$，$\overline A$表示$A$不会发生。

其次，对于事件$A$及事件$B$，定义两个新事件：
用$A \cap B$或$AB$表示所有同时属于$A$及$B$的样本点的集合，称它为$A$与$B$的交，事件$AB$表示事件$A$与事件$B$同时发生。
用$A \cup B$表示至少属于$A$或$B$中的一个的所有样本点的集合，称它为$A$与$B$的并，事件$A\cup B$表示事件$A$或事件$B$或它的二者发生，也始表示事件$A$与事件$B$至少发生一个。

若$AB=\varnothing$，则表示$A$与$B$不可能同时发生，称$A$与$B$互不相容。样本点是互不相容的。

以后，对于互不相容事件$A$与$B$， 我们称它们的并为和，并记作$A+B$。

用$A-B$表示包含在$A$中而不包含在$B$中的样本点全体，称之为$A$与$B$的差，事件$A-B$表示事件$A$发生而事件$B$不发生，显然$A-B=A \overline B$。

在进行事件的运算时，关于它们的顺序作如下约定：先进行逆的运算，再进行交的运算，最后才进行并或差的运算。

用上面的记号可以把对立事件之间的关系表述如下：$A \cup \overline A=\Omega$，$A \cap \overline A=\varnothing$，这也可以作为对立事件的定义。显然$\overline A=\Omega - A$。

将上面定义推广到多个事件的场合。
例如，对于$n$个事件$A_1,A_2,...,A_n$，用$A_1 \cup A_2 \cup ... \cup A_n$或 $\cup_{i=1}^nA_i$表示$A_1,A_2,...,A_n$中至少发生一个，称为$A_1,A_2,...,A_n$的并，特别当$A_1,A_2,...,A_n$两两互不相容时，并称为和，记作$A_1+A_2+...+A_n$或$\sum_{i=1}^nA_i$，用$A_1A_2...A_n$或$\cap_{i=1}^nA_i$表示$A_1,A_2,...,A_n$同时发生等等。
对于可列个事件的场合， 我们定义：

$$\bigcup_{i=1}^\infty A_i= \lim_{n->\infty} \bigcup_{i=1}^n A_i$$
$$\bigcap_{i=1}^\infty A_i = \lim_{n->\infty} \bigcap_{i=1}^n A_i$$

Venn图：

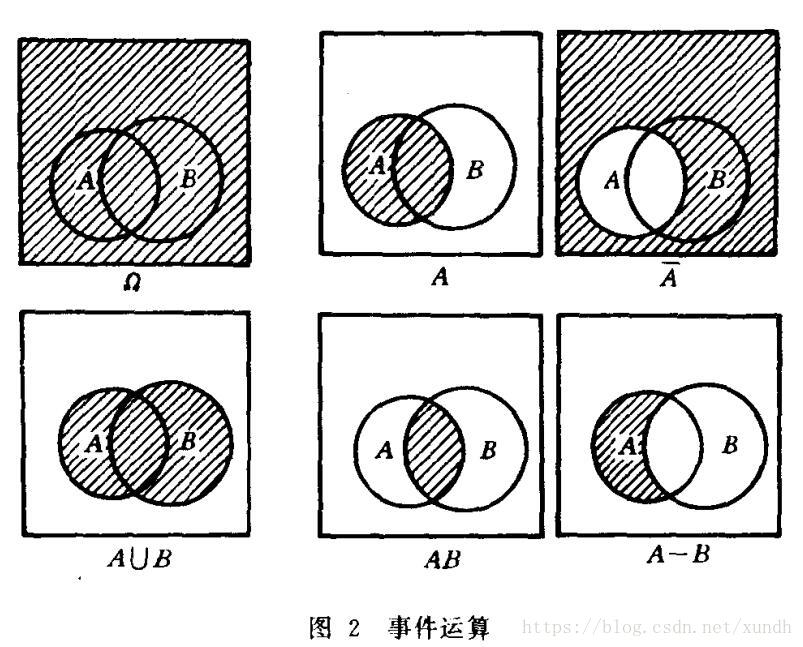
熟悉集合论的读者可能会发现，事件间的关系及运算与集合论中或布尔（Boole）代数中集合的关系及运算是完全相似的，而且这个相似在建立概率论的严格数学基础时非常重要。

【例6】 若$A,B,C$是三个事件，则
1. $A$发生而$B$与$C$都不发生可以表示为：$A\overline B \overline C$或$A-B-C$ 或 $A-(B\cup C)$；
2. $A$与$B$都发生而$C$不发生可以表示为：$AB\overline C$或 $AB-C$或$AB-ABC$；
3. 所有这三个事件都发生可以表示为：$ABC$；
4. 这三个事件恰好发生一个可以表示为：$A\overline B \overline C + \overline A B \overline C + \overline A \overline B C$；
5. 这三个事件恰好发生两个可以表示为：$AB\overline C + A\overline B C + \overline A BC$
6. 这三个事件中至少发生一个可以表示为：$A\cup B\cup C$或$A\overline B \overline C + \overline A B \overline C + \overline {AB} C + AB\overline C + A \overline B C + \overline A BC + ABC$

对于事件的运算成立下列关系式：

1. 交换律：$A\cup B = B \cup A$，$AB=BA$
2. 结合律：$(A\cup B)\cup C = A\cup(B\cup C),(AB)C=A(BC)$
3. 分配律：$(A\cup B)\cap C = AC \cup BC$,$(A\cap B)\cup C = (A \cup C)\cap (B \cup C)$
4. 德莫根（De Morgan）定理：
   $$\overline A_1 \overline{\bigcup A_2} = \overline A_1 \bigcap \overline A_2$$
   $$\overline{A_1 \bigcap A_2} = \overline A_1 \bigcup \overline A_2$$
   对于$n$个事件，甚至对于可列个事件，德莫根定理也成立。

四、有限样本空间

我们先考虑只有有限个样本点的样本空间，这种样本空间称为有限样本空间。这是最简单的样本空间，研究它有助于深入研究更为复杂的样本空间。
若 $\Omega$是有限样本空间，其样本点为 $E_1,E_2,...,E_n$，在这种场合可以把$\Omega$的任何子集都当作事件。在这种样本空间中引进概率，只要对每个样本点$E_i$，给定一个数与它对应，此数称为$E_i$的概率，并记之为$P(E_i)$，它是非负的，而且满足：

$$P(E_1) + P(E_2) +...+P(E_n)=1$$
这样，我们对样本点定义了概率，用它来试题每个样本点出现的可能性的大小。由此出发，我们不难定义更为一般的事件的概率。

定义1.2.1任何事件$A$的概率$P(A)$是$A$中各样本点的概率之和。

按照这个定义，显然有$P(\Omega)=1,0 \le P(A) \le 1$

把上面做法推广到有可列个样本点的样本空间是不难的，这种空间称为离散样本空间。但是当把上面做法推广到不可列个样本点的场合，则会遇到实质性的困难。