基础-数学-最大后验概率(MAP)maximum a posteriori

转载自 (http://blog.csdn.net/mafeichao/article/details/6403008)

在统计学中，最大后验（英文为Maximum a posteriori，缩写为MAP）估计方法根据经验数据获得对难以观察的量的点估计。它与最大似然估计中的 Fisher 方法有密切关系，但是它使用了一个增大的优化目标，这种方法将被估计量的先验分布融合到其中。所以最大后验估计可以看作是规则化（regularization）的最大似然估计。

假设我们需要根据观察数据 x 估计没有观察到的总体参数 θ，让 f 作为 x 的采样分布，这样 f(x | θ) 就是总体参数为θ 时 x 的概率。函数

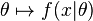
即为似然函数，其估计

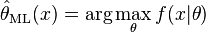
就是 θ 的最大似然估计。

假设 θ 存在一个先验分布 g，这就允许我们将 θ 作为 贝叶斯统计（en:Bayesian statistics）中的随机变量，这样 θ的后验分布就是：

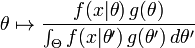
其中 Θ 是 g 的domain，这是贝叶斯定理（en: Bayes' theorem）的直接应用。

最大后验估计方法于是估计 θ 为这个随机变量的后验分布的mode：

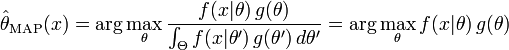
后验分布的分母与 θ 无关，所以在优化过程中不起作用。注意当前验 g 是 uniform（也就是常函数）时最大后验估计与最大似然估计重和。

最大后验估计可以用以下几种方法计算：

1. 解析方法，当后验分布的模能够用 closed form 方式表示的时候用这种方法。当使用en:conjugate prior 的时候就是这种情况。
2. 通过如共扼积分法或者牛顿法这样的数值优化方法进行，这通常需要一阶或者导数，导数需要通过解析或者数值方法得到。
3. 通过 期望最大化算法 的修改实现，这种方法不需要后验密度的导数。

尽管最大后验估计与 Bayesian 统计共享前验分布的使用，通常并不认为它是一种 Bayesian 方法，这是因为最大后验估计是点估计，然而 Bayesian 方法的特点是使用这些分布来总结数据、得到推论。Bayesian 方法试图算出后验均值或者中值以及posterior interval，而不是后验模。尤其是当后验分布没有一个简单的解析形式的时候更是这样：在这种情况下，后验分布可以使用 Markov chain Monte Carlo 技术来模拟，但是找到它的模的优化是很困难或者是不可能的。