先抛出信息熵公式如下:
其中P(xi)代表随机事件X为xi的概率,下面来逐步介绍信息熵的公式来源!
2 信息量
信息量是对信息的度量,就跟时间的度量是秒一样,当我们考虑一个离散的随机变量x的时候,当我们观察到的这个变量的一个具体值的时候,我们接收到了多少信息呢?
多少信息用信息量来衡量,我们接受到的信息量跟具体发生的事件有关。
信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大,如湖南产生的地震了;
越大概率的事情发生了产生的信息量越小,如太阳从东边升起来了(肯定发生嘛,没什么信息量)。这很好理解!
3 例子
脑补一下我们日常的对话:
师兄走过来跟我说,立波啊,今天你们湖南发生大地震了。
我:啊,不可能吧,这么重量级的新闻!湖南多低的概率发生地震啊!师兄,你告诉我的这件事,信息量巨大,我马上打电话问问父母什么情况。
又来了一个师妹:立波师兄,我发现了一个重要情报额,原来德川师兄有女朋友额~德川比师妹早进一年实验室,全实验室同学都知道了这件事。我大笑一声:哈哈哈哈,这件事大家都知道了,一点含金量都没有,下次八卦一些其它有价值的新闻吧!orz,逃~
因此一个具体事件的信息量应该是随着其发生概率而递减的,且不能为负。
但是这个表示信息量函数的形式怎么找呢?
随着概率增大而减少的函数形式太多了!不要着急,我们还有下面这条性质
如果我们有俩个不相关的事件x和y,那么我们观察到的俩个事件同时发生时获得的信息应该等于观察到的事件各自发生时获得的信息之和,即:
h(x,y) = h(x) + h(y)
由于x,y是俩个不相关的事件,那么满足
p(x,y) = p(x)*p(y).
根据上面推导,我们很容易看出h(x)一定与p(x)的对数有关(因为只有对数形式的真数相乘之后,能够对应对数的相加形式,可以试试)。因此我们有信息量公式如下:
下面解决俩个疑问?
(1)为什么有一个负号
其中,负号是为了确保信息量一定是正数或者是0,总不能为负数吧!
(2)为什么底数为2
这是因为,我们只需要信息量满足低概率事件x对应于高的信息量。那么对数的选择是任意的。我们只是遵循信息论的普遍传统,使用2作为对数的底!
4 信息熵
下面我们正式引出信息熵。
信息量度量的是一个具体事件发生了所带来的信息,而熵则是在结果出来之前对可能产生的信息量的期望
考虑该随机变量的所有可能取值,即所有可能发生事件所带来的信息量的期望。即
转换一下为:
最终我们的公式来源推导完成了。
这里我再说一个对信息熵的理解。信息熵还可以作为一个系统复杂程度的度量,如果系统越复杂,出现不同情况的种类越多,那么他的信息熵是比较大的。
如果一个系统越简单,出现情况种类很少(极端情况为1种情况,那么对应概率为1,那么对应的信息熵为0),此时的信息熵较小。
这也就是我理解的信息熵全部想法,希望大家指错交流。也希望对大家理解有帮助~
参考:
“熵”的通俗解释 - 七月在线
关于信息熵的个人通俗的理解
原文来源:










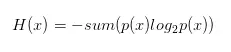
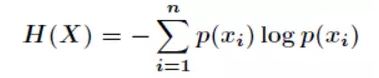
















 521
521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








