pacf系数计算

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
plt.rcParams['font.family'] = 'Songti SC'  # 显示中文标签
#from matplotlib.font_manager import FontProperties
#font =FontProperties(fname = '/Users/cloudwise/Documents/字体/simsun.ttf')
%matplotlib inline

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import pacf, pacf_ols, pacf_yw
import statsmodels as sm
from scipy.linalg import toeplitz
from statsmodels.regression.linear_model import OLS, yule_walker

公式

statsmodels.tsa.stattools.pacf的计算方式
参考：https://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#yule_walker

$$\begin{gathered} Yule-Walker方程，系数求法 \\ input1:ts \\ input2:order \\ n=len(ts) \\ k\in [0,1,2,3,...,order] \\ {r}_k=\frac{t{s}_1\ast t{s}_{k+1}+t{s}_2\ast t{s}_{k+2}+t{s}_3\ast t{s}_{k+3}+...+t{s}_{n-k}\ast t{s}_n}{n-k} \end{gathered}$$

$$R=\left[\begin{array}{ccccc}{r}_0& r_1& r_2& ...& r_{order-1}\\ r_1& r_0& r_1& ...& r_{order-2}\\ r_2& r_1& r_0& ...& r_{order-3}\\ ...& & ...& ...& ...\\ r_{order-1}& r_{order-2}& r_{order-3}& ...& r_0\end{array}\right]$$

$R为toeplitz矩阵$

$$\begin{gathered} 多元函数，求解rho \\ {R}_{order\ast order}\ast rh{o}_{order\ast 1}^T=[r_1,r_2,r_3,...,r_{order}{]}_{order\ast 1}^T \end{gathered}$$
即
$$\begin{gathered} r_0\ast rh{o}_0+r_1\ast rh{o}_1+r_2\ast rh{o}_2+...+r_{order-1}\ast rh{o}_{order-1}=r_1 \\ {r}_1\ast rh{o}_0+r_0\ast rh{o}_1+r_1\ast rh{o}_2+...+r_{order-2}\ast rh{o}_{order-1}=r_2 \\ ...... \\ {r}_{order-1}\ast rh{o}_0+r_{order-2}\ast rh{o}_1+r_{order-3}\ast rh{o}_2+...+r_{r0}\ast rh{o}_{order-1}=r_{order} \end{gathered}$$

$$sigmasq=r_0-\sum _{i=1}^{order}(r_i\ast rh{o}_{i-1})$$

$$第order阶的pacf值：rh{o}_{order-1}$$

示例

a = np.array([1,2,3,4,5])
#a = a - np.mean(a)
n = len(a)

plot_pacf(a)

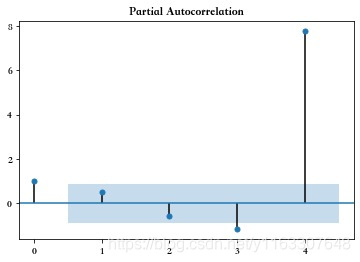
pacf_yw(a, nlags=4, method='unbiased')

order = 4

print(sm.regression.yule_walker(a, order=order))

a = a - np.mean(a)

adj_needed = 1
r = np.zeros(order+1, np.float64)
r[0] = (a ** 2).sum() / n
for k in range(1, order+1):
    r[k] = (a[0:-k] * a[k:]).sum() / (n - k * adj_needed)

R = toeplitz(r[:-1])
rho = np.linalg.solve(R, r[1:])
print(rho, rho[-1])

(array([ 9.  , -2.25, -2.25,  7.75]), 4.330127018922193)
[ 9.   -2.25 -2.25  7.75] 7.749999999999999

第四阶的系数为：7.75
rho[-1]：7.749999999999999
相等

对比pacf中yule_walker 和 ols方法的差异

plot_pacf(a)

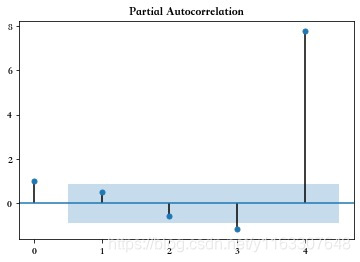
plot_pacf(a, method = 'ols')

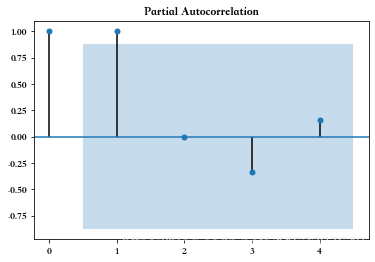
?plot_pacf

print(pacf_yw(a, nlags=4, method='unbiased'))
print(pacf_yw(a, nlags=4, method='mle'))

[ 1.          0.5        -0.55555556 -1.14285714  7.75      ]
[ 1.          0.4        -0.30952381 -0.29467085 -0.17966102]

print(pacf_ols(a, nlags=4, efficient=True,  unbiased=True))
print(pacf_ols(a, nlags=4, efficient=True,  unbiased=False))
print(pacf_ols(a, nlags=4, efficient=False,  unbiased=True))
print(pacf_ols(a, nlags=4, efficient=False,  unbiased=False))

[ 1.00000000e+00  1.25000000e+00 -2.60138922e-16 -8.33333333e-01
  8.06451613e-01]
[ 1.00000000e+00  1.00000000e+00 -1.56083353e-16 -3.33333333e-01
  1.61290323e-01]
[ 1.          2.5         0.         -2.5        -3.33333333]
[ 1.          2.          0.         -1.         -0.66666667]

示例

from statsmodels.tsa.tsatools import lagmat

xlags, x0 = lagmat(a_mean, 4, original='sep', trim='both')

a_mean

array([-2., -1.,  0.,  1.,  2.])

xlags

array([[ 1.,  0., -1., -2.]])

x0

array([[2.]])

pacf_ols的计算

#使用最小二乘求1阶系数时
#结果与pacf_ols一阶系数不一致
np.linalg.lstsq(np.array([[-2],[-1],[0],[1]]), np.array([-1,0,1,2]), rcond=None)[0]

array([0.66666667])

#结果与pacf_ols一阶系数一致
np.linalg.lstsq(xlags[:, :1],x0, rcond=None)[0][-1]

array([2.])

#结果与pacf_ols 2阶系数一致
np.linalg.lstsq(xlags[:, :2],x0, rcond=None)[0][-1]

array([0.])

#结果与pacf_ols 3阶系数一致
np.linalg.lstsq(xlags[:, :3],x0, rcond=None)[0][-1]

array([-1.])

#结果与pacf_ols 4阶系数一致
np.linalg.lstsq(xlags[:, :4],x0, rcond=None)[0][-1]

array([-0.66666667])

np.linalg.lstsq([[1,0,-1,-2]],[[2]], rcond=None)[0][-1]

array([-0.66666667])

$$\begin{gathered} 从上述过程可以看出，使用pacf\_ols时，系数的解a_k来自： \\ {x}_t=a_1\ast xt-1+a_2\ast xt-2+a_3\ast xt-3+...+a_k\ast xt-k \\ 而非： \end{gathered}$$

$$\begin{gathered} x_t=a_1\ast x_{t-1}+a_2\ast x_{t-2}+a_3\ast x_{t-3}+...+a_k\ast x_{t-k} \\ {x}_{t-1}=a_1\ast x_{t-1-1}+a_2\ast x_{t-1-2}+a_3\ast x_{t-1-3}+...+a_k\ast x_{t-1-k} \\ {x}_{t-2}=a_1\ast x_{t-2-1}+a_2\ast x_{t-2-2}+a_3\ast x_{t-2-3}+...+a_k\ast x_{t-2-k} \\ ... \\ {x}_k=a_1\ast x_{k-1}+a_2\ast x_{k-2}+a_3\ast x_{k-3}+...+a_k\ast x_0 \end{gathered}$$

pacf_ols的计算方式与http://www-stat.wharton.upenn.edu/~steele/Courses/956/ResourceDetails/YWSourceFiles/YW-Eshel.pdf 中描述的不同

pacf_yule的计算

pacf_yw(a_mean, nlags=1, method='mle')

array([1. , 0.4])

yule_walker(a_mean, 1, method='mle')

(array([0.4]), 1.296148139681572)

参考文献中：
一阶系数

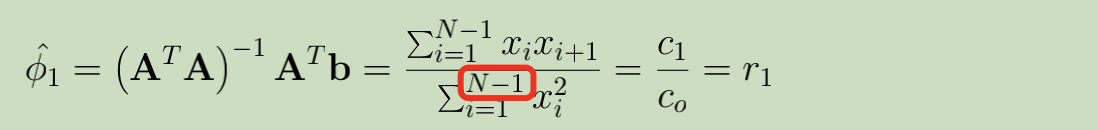
参考文献中，分母为${\sum }_{i=1}^{N-k}{x}_i^2$
pacf_yule中分母为${\sum }_{i=1}^N{x}_i^2$

问题

相关资料上都有这样的描述：
”PACF相当于在计算X(t)和X(t-h)的相关性的时候，挖空在(t-h,t)上所有数据点对X(t)的影响，去反映X(t-h)和X(t)之间真正的相关性“
怎么理解𝑌𝑢𝑙𝑒−𝑊𝑎𝑙𝑘𝑒𝑟方程或最小二乘计算出来的系数是挖空了(t-h,t)上所有数据点对X(t)的影响的？

𝑌𝑢𝑙𝑒−𝑊𝑎𝑙𝑘𝑒𝑟或最小二乘的计算结果是一样的。𝑌𝑢𝑙𝑒−𝑊𝑎𝑙𝑘𝑒𝑟方程的提出为了优化计算过程，减少计算量

单从pacf的计算方式看，$pac{f}_k$就是第k阶的自回归系数。所谓的‘挖空了(t-h,t)上所有数据点对X(t)的影响’，指的是做自回归
$x_{i+1}={\phi }_1{x}_i+{\phi }_2{x}_{i-1}+\cdot \cdot \cdot +{\phi }_p{x}_{i-p+1}+\xi i+1$ 时，将x_{i-1}到x_{i-k}都视作因变量

$pac{f}_k={\phi }_k$

参考：
http://www-stat.wharton.upenn.edu/~steele/Courses/956/ResourceDetails/YWSourceFiles/YW-Eshel.pdf