在时间序列分析中,自相关函数(Autocorrelation Function,ACF)和偏自相关函数(Partial Autocorrelation Function,PACF)是重要的工具,用于描述数据的相关性结构,帮助我们识别和选择合适的模型。下面详细介绍ACF和PACF的概念、数学表达式和应用。
下文涉及到的模型的缩写:
- AR:Autoregressive Model,即自回归模型
- MA:Moving Average Model,移动平均模型
- ARMA:Autoregressive Moving Average Model, 自回归移动平均模型
- ARIMA: Autoregressive Integrated Moving Average Model,差分自回归移动平均模型
这些模型均常用于时间序列分析,将在下一期分享中介绍
自相关函数(ACF)
**定义:**自相关函数描述了时间序列在不同滞后期数(Lag)下的相关性,即序列与其自身滞后值之间的线性相关程度。它衡量了当前值与过去值之间的关系。
关于滞后期数的进一步解释
在时间序列分析中,我们经常关注当前值 $ Y_t $ 与其过去某个时刻的值 $ Y_{t - k} $ 之间的关系。**滞后 $ k $ 期(Lag $ k $)**就代表了当前时间点 $ t $ 与过去第 $ k $ 个时间点 $ t - k $ 之间的时间间隔,例如:
滞后 k = 1 期:当前值与前一天(或前一单位时间)的值之间的关系。
滞后 k = 2 期:当前值与前两天(或前两个单位时间)的值之间的关系。
数学表达式:
对于给定的时间序列 $ {Y_t} $,其均值为 $ \mu ,在滞后 ,在滞后 ,在滞后 k $ 期下的自相关函数 ρ ( k ) \rho(k) ρ(k)定义为:
ρ ( k ) = γ ( k ) γ ( 0 ) \rho(k) = \frac{\gamma(k)}{\gamma(0)} ρ(k)=γ(0)γ(k)
其中,$ \gamma(k) $ 是滞后 $ k $ 的自协方差函数,定义为:
γ ( k ) = Cov ( Y t , Y t − k ) = E [ ( Y t − μ ) ( Y t − k − μ ) ] \gamma(k) = \text{Cov}(Y_t, Y_{t-k}) = E[(Y_t - \mu)(Y_{t-k} - \mu)] γ(k)=Cov(Yt,Yt−k)=E[(Yt−μ)(Yt−k−μ)]
而 $ \gamma(0) $ 是零滞后(即同一时间点)的自协方差,等于序列的方差:
γ ( 0 ) = Var ( Y t ) = E [ ( Y t − μ ) 2 ] \gamma(0) = \text{Var}(Y_t) = E[(Y_t - \mu)^2] γ(0)=Var(Yt)=E[(Yt−μ)2]
因此,自相关函数可表示为:
ρ ( k ) = E [ ( Y t − μ ) ( Y t − k − μ ) ] E [ ( Y t − μ ) 2 ] \rho(k) = \frac{E[(Y_t - \mu)(Y_{t-k} - \mu)]}{E[(Y_t - \mu)^2]} ρ(k)=E[(Yt−μ)2]E[(Yt−μ)(Yt−k−μ)]
样本自相关函数::在实际应用中,我们使用样本数据来估计自相关函数,得到样本自相关系数 $ r(k) $:
r ( k ) = ∑ t = k + 1 N ( Y t − Y ˉ ) ( Y t − k − Y ˉ ) ∑ t = 1 N ( Y t − Y ˉ ) 2 r(k) = \frac{\sum_{t=k+1}^{N} (Y_t - \bar{Y})(Y_{t-k} - \bar{Y})}{\sum_{t=1}^{N} (Y_t - \bar{Y})^2} r(k)=∑t=1N(Yt−Yˉ)2∑t=k+1N(Yt−Yˉ)(Yt−k−Yˉ)
其中:
- $ N $:样本容量,即数据点的数量;
- $ \bar{Y} $:样本均值,计算方式为 $ \bar{Y} = \frac{1}{N} \sum_{t=1}^{N} Y_t $。
解释:
- 当 $ \rho(k) > 0 $ 时,表示当前值与滞后 $ k $ 期的值正相关;
- 当 $ \rho(k) < 0 $ 时,表示当前值与滞后 $ k $ 期的值负相关;
- $ \rho(k) $ 的绝对值越大,相关性越强。
偏自相关函数(PACF)
**定义:**偏自相关函数(Partial Autocorrelation Function,PACF)用于度量时间序列中当前值 Y t Y_t Yt与滞后 k期的值 Y t − k Y_{t-k} Yt−k之间的纯粹相关性,排除了介于两者之间的所有中间滞后项($ Y_{t-1}, Y_{t-2}, …, Y_{t-k+1} $)的干扰。
简单理解,就是类似于偏导数的概念
数学表达式:
对于滞后阶数 $ k $,偏自相关函数 $ \phi(k) $ 定义为:
ϕ ( k ) = Corr ( Y t − P k − 1 ( Y t ) , Y t − k − P k − 1 ( Y t − k ) ) \phi(k) = \text{Corr}(Y_t - P_{k-1}(Y_t), Y_{t-k} - P_{k-1}(Y_{t-k})) ϕ(k)=Corr(Yt−Pk−1(Yt),Yt−k−Pk−1(Yt−k))
其中:
- $ P_{k-1}(Y_t) $ 是基于 $ Y_{t-1}, Y_{t-2}, …, Y_{t-k+1} $ 的 Y t Y_t Yt最小二乘预测值;
- 同样的$ P_{k-1}(Y_{t-k}) $ 是基于 $ Y_{t-1}, Y_{t-2}, …, Y_{t-k+1} $ 的 Y t − k Y_{t-k} Yt−k最小二乘预测值;
- $ \text{Corr} $ 表示相关系数。
深度解析:
-
在时间序列分析中,为了理解变量之间的纯粹相关性,我们需要排除其他变量的影响。
-
通过对 $ Y_t $ 和 $ Y_{t - k} $ 分别进行线性回归,我们得到的残差代表了各自变量中不被中间滞后项解释的部分。
-
$ Y_t - P_{k-1}(Y_t) $ 是 $ Y_t $ 对 $ Y_{t-1}, \dots, Y_{t - k + 1} $ 进行线性回归后的残差,表示在剔除了中间滞后项的影响后,$ Y_t $ 中剩余的部分。
-
$ Y_{t - k} - P_{k-1}(Y_{t - k}) $ 同理,是 $ Y_{t - k} $ 对中间滞后项进行线性回归后的残差。
-
-
偏自相关系数 $ \phi(k) ∗ ∗ 就是这两个残差之间的相关系数,反映了在剔除中间滞后项影响后, ** 就是这两个残差之间的相关系数,反映了在剔除中间滞后项影响后, ∗∗就是这两个残差之间的相关系数,反映了在剔除中间滞后项影响后, Y_t $ 与 $ Y_{t - k} $ 之间的纯净**相关性。
计算方法:偏相关系数的计算比较复杂,可以通过递归的方法计算,例如Yule-Walker方程或Durbin-Levinson算法。
Yule-Walker方程:
对于自回归模型AR($ p $),偏自相关系数 $ \phi_{kk} $ 可以通过以下递归关系计算:
-
初始条件:
ϕ 11 = r ( 1 ) \phi_{11} = r(1) ϕ11=r(1)
-
递归公式:
ϕ k k = r ( k ) − ∑ j = 1 k − 1 ϕ k − 1 , j r ( k − j ) 1 − ∑ j = 1 k − 1 ϕ k − 1 , j r ( j ) \phi_{kk} = \frac{r(k) - \sum_{j=1}^{k-1} \phi_{k-1,j} r(k - j)}{1 - \sum_{j=1}^{k-1} \phi_{k-1,j} r(j)} ϕkk=1−∑j=1k−1ϕk−1,jr(j)r(k)−∑j=1k−1ϕk−1,jr(k−j)
其中,$ \phi_{k-1,j} $ 是第 $ k - 1 $ 阶的偏自相关系数。
解释:
- 偏自相关函数在滞后阶数超过实际的自回归阶数 $ p $ 后,偏自相关系数将迅速衰减至零(截尾)。
- Yule-Walker方程中,偏自相关系数常表达为 $ \phi_{kk} $,但实际上与 $ \phi(k) 是同一种概念。而在这里使用 是同一种概念。而在这里使用 是同一种概念。而在这里使用 \phi_{kk} $主要是为了在递归计算和矩阵表示中保持符号的一致性,特别是在多阶参数递推中。例如, 在递归计算过程中, $ \phi_{kk} $表示第 k 阶AR模型中,第 k 个自回归系数。
PACF计算示例:
假设我们要计算滞后2期的偏自相关系数 $ \phi(2) $:
-
对 $ Y_t $ 和 $ Y_{t-2} $ 进行线性回归:
-
回归 $ Y_t $ 对 $ Y_{t-1} $:
Y t = β 0 + β 1 Y t − 1 + ε t Y_t = \beta_0 + \beta_1 Y_{t-1} + \varepsilon_t Yt=β0+β1Yt−1+εt
得到预测值 P 1 ( Y t ) = β ^ 0 + β ^ 1 Y t − 1 P_1(Y_t) = \hat{\beta}_0 + \hat{\beta}_1 Y_{t-1} P1(Yt)=β^0+β^1Yt−1。
-
回归 $ Y_{t-2} $ 对 $ Y_{t-1} $:
Y t − 2 = γ 0 + γ 1 Y t − 1 + ε t − 2 Y_{t-2} = \gamma_0 + \gamma_1 Y_{t-1} + \varepsilon_{t-2} Yt−2=γ0+γ1Yt−1+εt−2
得到预测值 P 1 ( Y t − 2 ) = γ ^ 0 + γ ^ 1 Y t − 1 P_1(Y_{t-2}) = \hat{\gamma}_0 + \hat{\gamma}_1 Y_{t-1} P1(Yt−2)=γ^0+γ^1Yt−1。
-
-
计算残差:
- $ e_t = Y_t - P_1(Y_t) $
- $ e_{t-2} = Y_{t-2} - P_1(Y_{t-2}) $
-
计算残差之间的相关系数:
- $ \phi(2) = \text{Corr}(e_t, , e_{t-2}) $
ACF和PACF在模型识别中的作用
总结一下:
-
**自相关函数(ACF)**衡量时间序列在不同滞后阶数下的相关性,帮助识别数据的移动平均特性。
-
**偏自相关函数(PACF)**衡量在控制中间滞后影响后的纯粹相关性,帮助识别数据的自回归特性。
-
ACF和PACF的结合使用,有助于确定时间序列模型的类型和阶数,为构建AR、MA、ARMA等模型提供依据。
ACF和PACF的观察方法:
- **ACF(自相关函数):**观察ACF图,确定自相关系数在不同滞后期下的显著性。
- 截尾特征: 在某个滞后期后,自相关系数迅速降为零。
- 拖尾特征: 自相关系数逐渐衰减,不立即降为零。
- **PACF(偏自相关函数):**观察PACF图,确定偏自相关系数在不同滞后期下的显著性。
- 截尾特征: 在某个滞后期后,偏自相关系数迅速降为零。
- 拖尾特征: 偏自相关系数逐渐衰减。
模型选择依据:
- AR模型: PACF截尾,ACF拖尾。
- MA模型: ACF截尾,PACF拖尾。
- ARMA模型: ACF和PACF均拖尾。
- 没有合适模型:ACF和PACF均截尾。
ACF和PACF图示例以及解读
以下使用的ACF和PACF来自网络:https://spssau.com/helps/conometricstudy/acfpacf.html
ACF图:
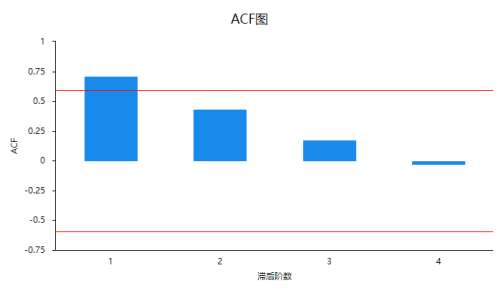
PACF图:

图片解读:
- 从自相关ACF图可知,可以理解其为4阶截尾,也或者理解为拖尾现象,但一般情况下4阶会比较大,因而暂认为当前数据为拖尾现象。
- 从偏自相关图PACF可以看出:从2阶开始快速趋近于0,意味着在2阶截尾(也可以看成是3阶截尾,或者4阶截尾均可)。结合判断标准可知:自相关图为拖尾,偏自相关图为2阶截尾。因此最终模型选择为AR(2)较为适合。
**关于上述ACF和PACF图的解读上,通常需要结合研究人员的主观判断加以定夺(并且很多时候可以有多个候选模型),没有绝对的标准。**此时研究人员可直接使用ARMA模型进行分析,并且对比AIC值等,选出最优的ARMA模型,比如本案例中可以建立出2个ARMA模型分别是:AR(3),AR(2),具体哪个更优则对比2个ARMA模型时的AIC值,那个模型的AIC值更小最终就使用哪个,如下表可以看出AR(3)相对更优(AIC值相对更小),因此最终使用AR(3)模型即可,与此同时,还可尝试结合其它模型比如AR(4)进行综合对比。
| 模型 | AIC值 |
|---|---|
| AR(3) | 135.561 |
| AR(2) | 143.059 |
注意事项
-
平稳性假设: ACF和PACF的理论基础是时间序列的平稳性,即均值和方差不随时间变化,自协方差只与滞后阶数有关。在计算ACF和PACF之前,确保数据平稳。如果数据非平稳,需通过差分或其他方法使其平稳。
-
统计显著性: 在绘制ACF和PACF图时,通常会加上显著性水平的置信区间(如95%置信区间)。如果自相关系数超出此区间,认为其显著不为零。
-
白噪声检验: 如果所有滞后阶数的自相关系数均在置信区间内,说明序列可能是白噪声。
-
模型比较: 可能需要尝试多种模型,利用信息准则(如AIC、BIC)选择最佳模型。


























 2300
2300

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










