几何角度理解：L1比L2范数更具有稀疏性的理解

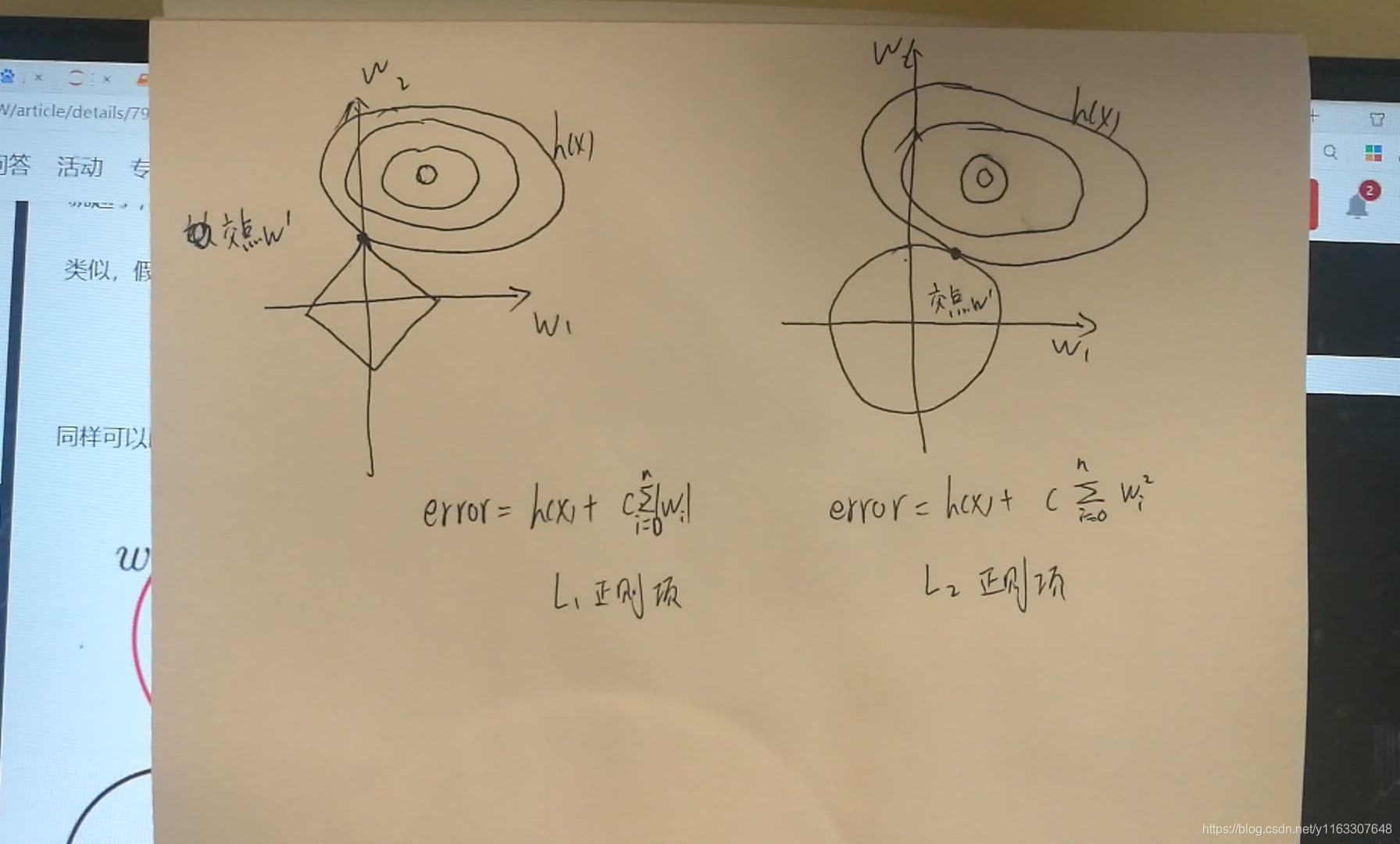
很多解释L1和L2稀疏性比较的文章都有上面这图。都说：因为L1和h(x)的交点更容易出现在轴上，所以会使得系数取0，获取稀疏的权重。但之前一直不理解，为什么交点就是最小误差的点呢？

这里记录下现在的理解：

error = h(x ) + C * L1
设h(x) = a, L1=b, 它们的等值线分别如下图所示

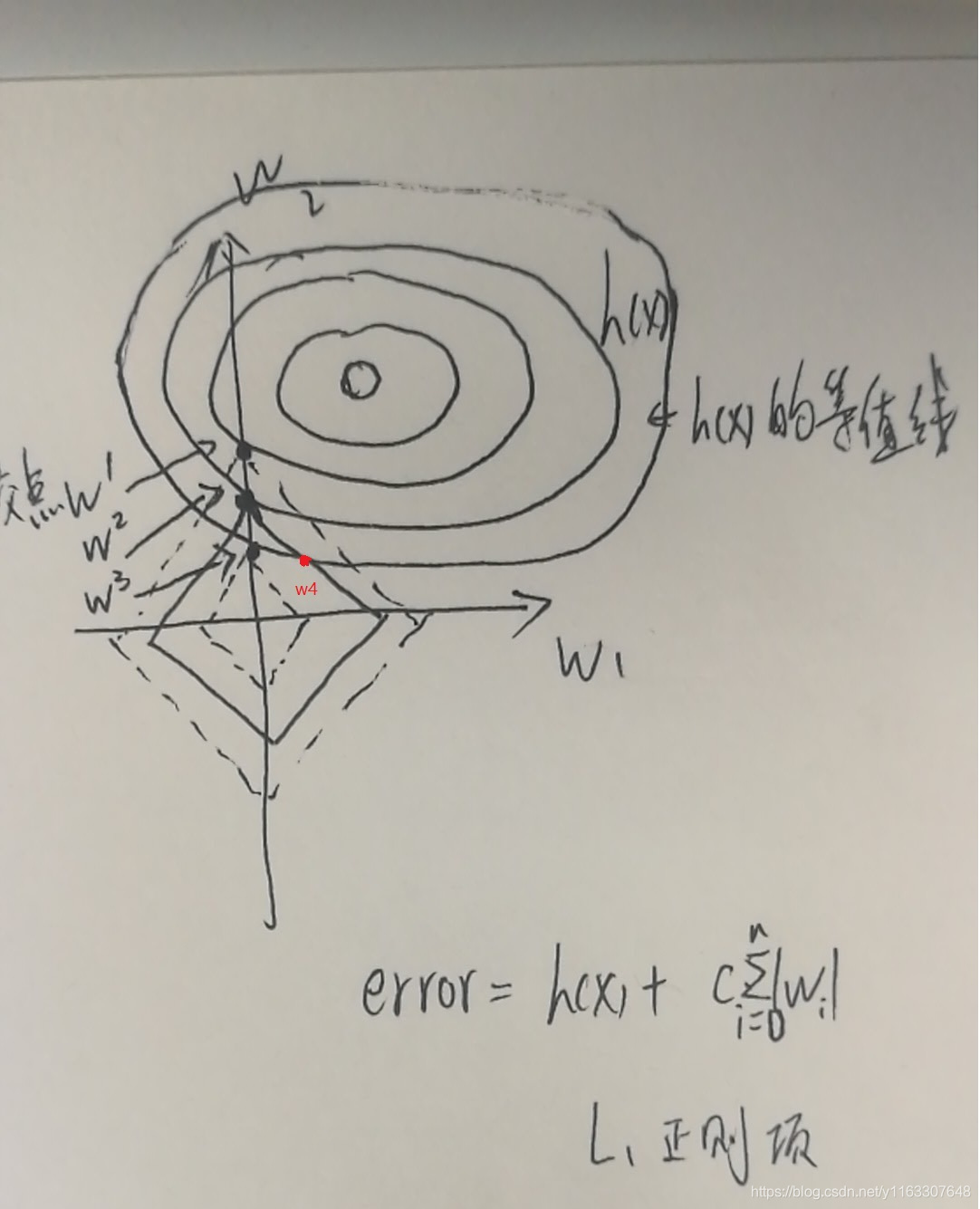
假设现在任取一个点w4，w4分别位于 h(w) = a1 和 L1=b1 上，所以当前 error = a1 + b1。从图上可以看到，w2和w4在L1的同一条等值线上，且h(w2)<h(w4) (h(w)的最小值点在椭圆中心)，所以当L1(w)的值固定时，显然w2是最优解。（有些时候h(w)和L1(w)的切点也会在w4这，这时，w4就是最优解了，不过这种情况比较少见）。这就解释了为什么交点容易产生在轴上。
对于w1，w2，w3的比较，从图上可以看出h(w)和L1(w)时互相冲突，h(w)增大，则L1(w)减少，反之亦然。（当h(w)的最小值点在L1(w)的方框内时，两者同时增大，缩小，不过因为要求min error，L1(w)的框会很快缩小，同时减少L1和h的值，直到h的最小值点不在L1的框内）。至于w1,w2,w3哪个更好，就要看C的值了。error = h(w) + C * L1(w)，通过C判断h(w) 和 L1(w)哪个更重要。