斐波那契数列
在数学中,斐波那契数列的定义是:
f
n
=
{
n
(
n
=
0
,
1
)
f
n
−
1
+
f
n
−
2
(
n
⩾
2
)
f_n=\left\{\begin{array}{lc}n&(n=0,1)\\f_{n-1}+f_{n-2}\;\;&(n\geqslant2\;\;\;)\end{array}\right.
fn={nfn−1+fn−2(n=0,1)(n⩾2)
很明显,这是一个递归定义,很多数据结构书中也拿斐波那契数列来讲解递归的过程。根据这个定义可以得到一个斐波那契数列:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | …… |
|---|---|---|---|---|---|---|---|---|---|---|
| 数列值 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | …… |
先讨论一下这个数列值如何用程序来产生,这是个递归定义,那肯定是可以用递归函数来生成这个数列了。
unsigned __int64 Fib(int n)
{
if (n <= 1)
return n;
else
return Fib(n - 1) + Fib(n - 2);
}
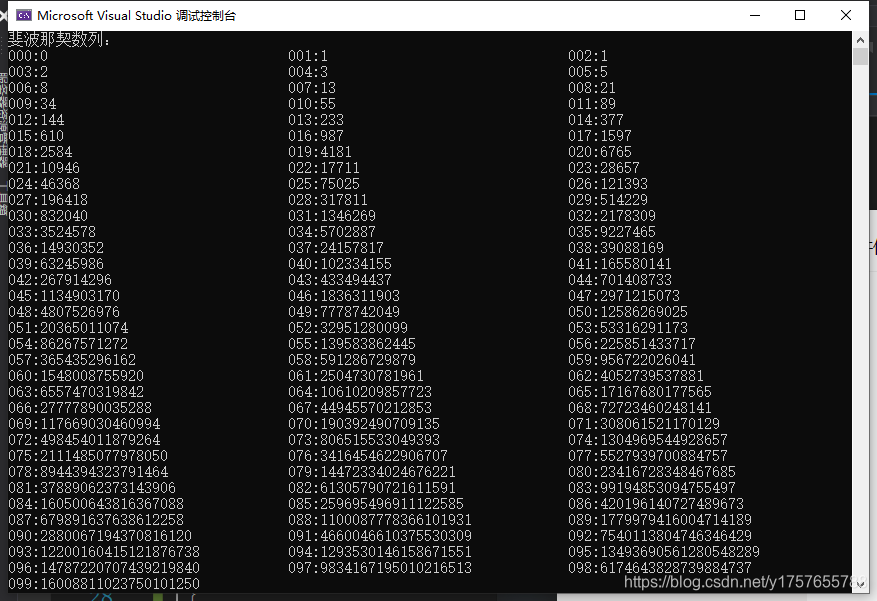
这几行代码非常简单,但是在实际过程中不可这么用。为什么?用这个函数生成长度为100的数列,跑一跑就知道了.
void main(void)
{
printf("斐波那契数列:\r\n");
for (int i = 0; i < 100; i++)
{
printf("%3d:%I64u \r\n", i,Fib(i));
}
}
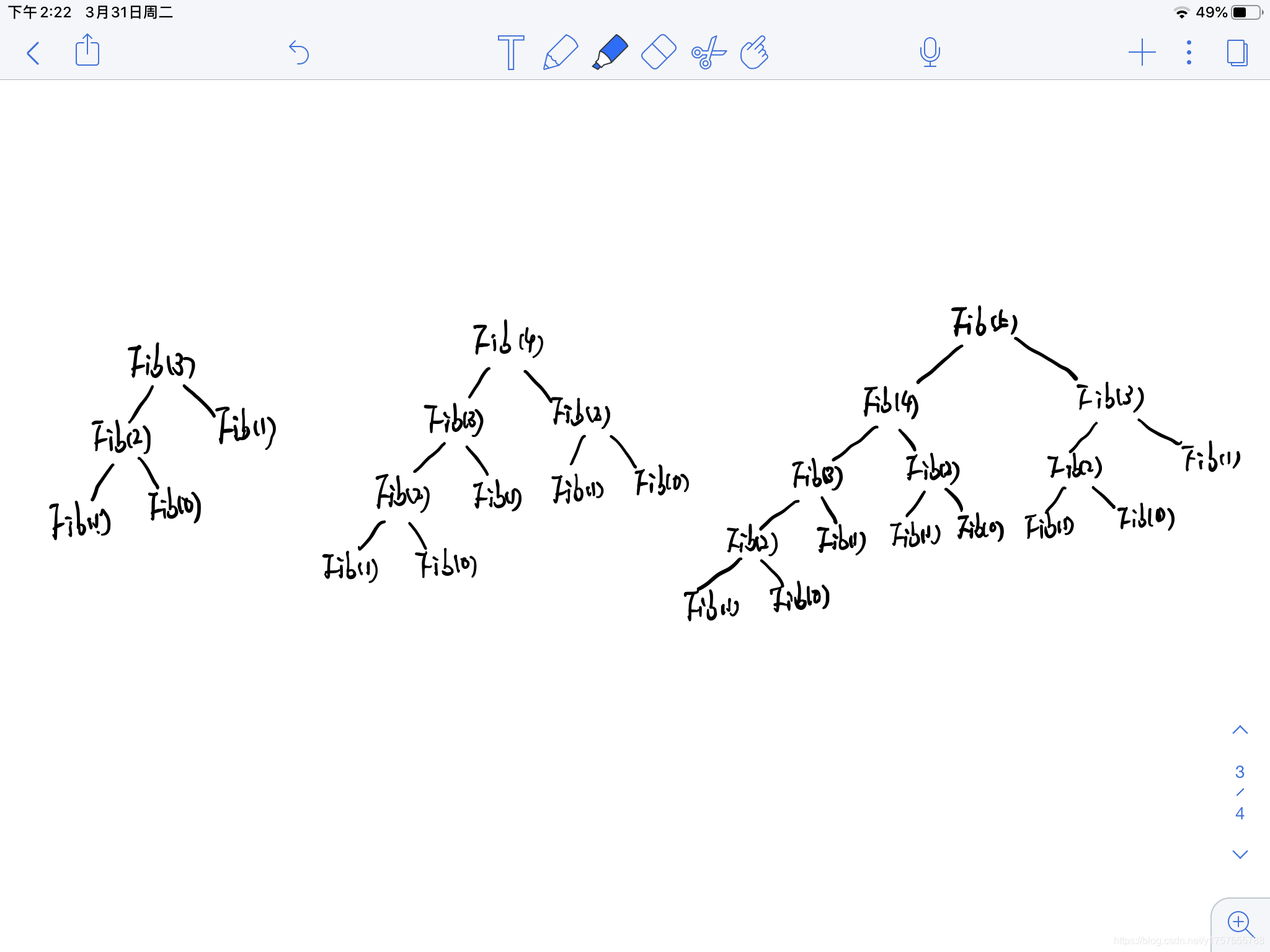
这总共不超过20行的代码,用一台六年前的笔记本整整跑了一个半小时,只计算到数列的第五十一个值 ,虽然笔记本性能一般,但是这几行代码异常耗时是有内层机理的。用这个方法计算一个斐波那契数列,越到后面越耗时,时间的增加就跟数列值的增加一样,后一个值的计算用时是前两个值计算用时的总和。以数列第3、4、5个值为例:
要计算
F
i
b
(
5
)
Fib(5)
Fib(5) 就要计算
F
i
b
(
4
)
Fib(4)
Fib(4) 和
F
i
b
(
3
)
Fib(3)
Fib(3),同样,要计算
F
i
b
(
4
)
Fib(4)
Fib(4) 就要计算
F
i
b
(
3
)
Fib(3)
Fib(3) 和
F
i
b
(
2
)
Fib(2)
Fib(2),一直到叶子节点,即
F
i
b
(
1
)
Fib(1)
Fib(1) 或
F
i
b
(
0
)
Fib(0)
Fib(0) 才一层层返回,也就是说
F
i
b
(
5
)
Fib(5)
Fib(5) 的计算重复了
F
i
b
(
4
)
Fib(4)
Fib(4) 和
F
i
b
(
3
)
Fib(3)
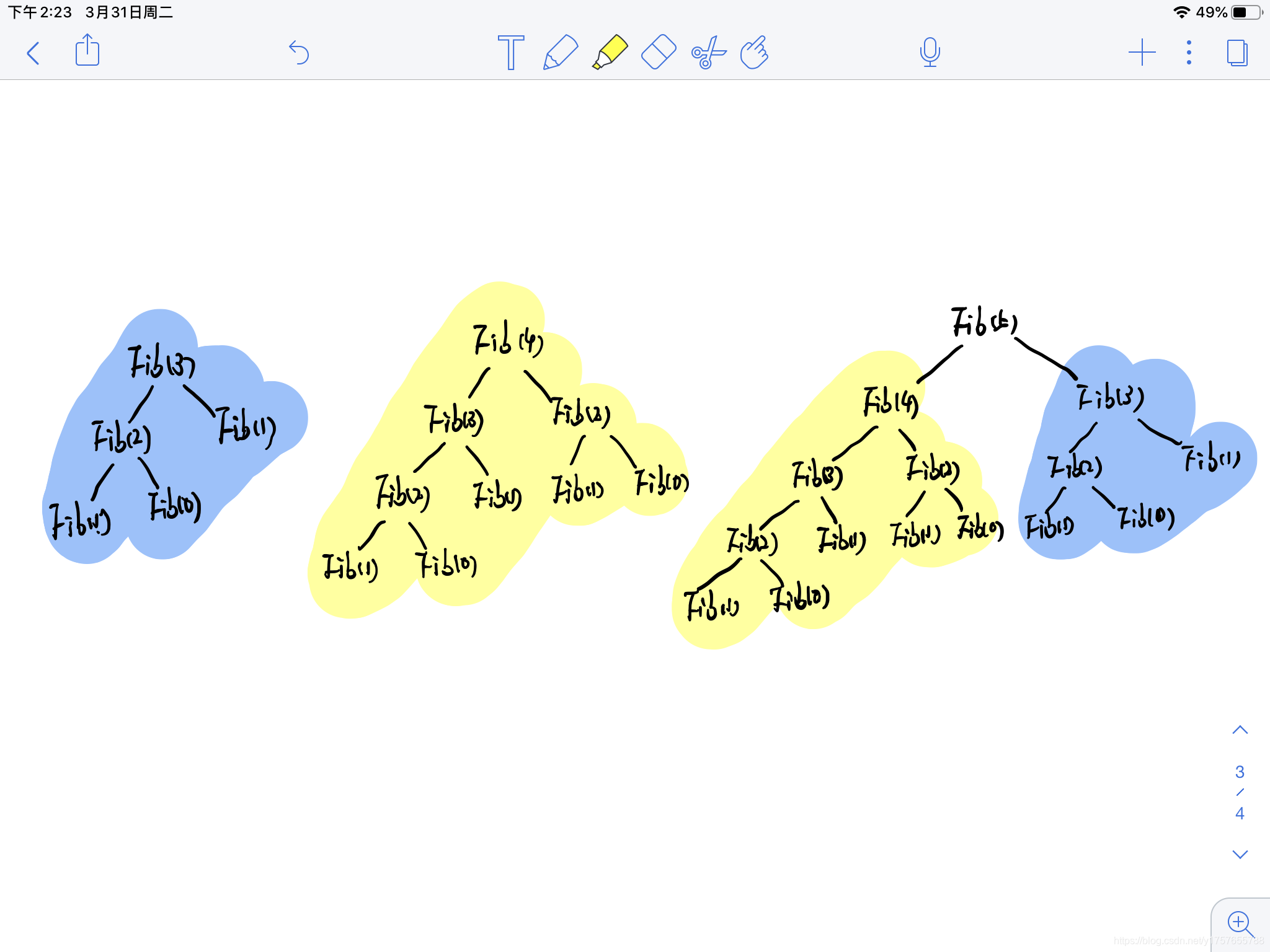
Fib(3) 的计算过程,做了大量的重复计算过程,而且这个增长接近2的指数级。
像斐波那契数列这样的递归计算不适用于实际,那就要想办法将它转化成其他形式,例如迭代运算。
| 数列值 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | …… |
|---|---|---|---|---|---|---|---|---|---|---|
| 第一次 | i i i | p p p | q q q | |||||||
| 第二次 | i i i | p p p | q q q | |||||||
| 第三次 | i i i | p p p | q q q | |||||||
| 第四次 | i i i | p p p | q q q | |||||||
| 第五次 | i i i | p p p | q q q | |||||||
| 第六次 | i i i | p p p | q q q |
通过 i i i, p p p, q = i + p q=i+p q=i+p往后移就可以得到数列中任意想要的值。写成代码:
unsigned __int64 Fib(int n)
{
unsigned __int64 i = 0, p = 1, q = 1;
if (n <= 1) return n;
else if (n == 2) return 1;
else
{
for (int j = 2; j < n; j++)
{
i = p;
p = q;
q = i + p;
}
return q;
}
}
程序跑完才发现,64位无符号整型仍然不够,还是产生了溢出。
去年研究生考试结束后在南京面试,笔试里就有一道斐波那契数列的程序题,一开始写的程序是动态申请一块内存作为数组,前两个值相加的和放到后一个单元里面,然后一直迭代下去,产生一组斐波那契数列。面试官就说如果数列很长呢,还能用动态申请的方式去生成这个数列吗?于是就写了迭代版本的Fib函数,面试官看了一会,好像还是没有get到他的要求。出了公司门一个瞬间有个念头:难道他想要我写出递归版本?他招的是嵌入式软件工程师啊。。亦或者是斐波那契数列的生成有更优的方法,但是本人愚钝。。。
斐波那契查找
斐波那契查找又是怎么回事呢?
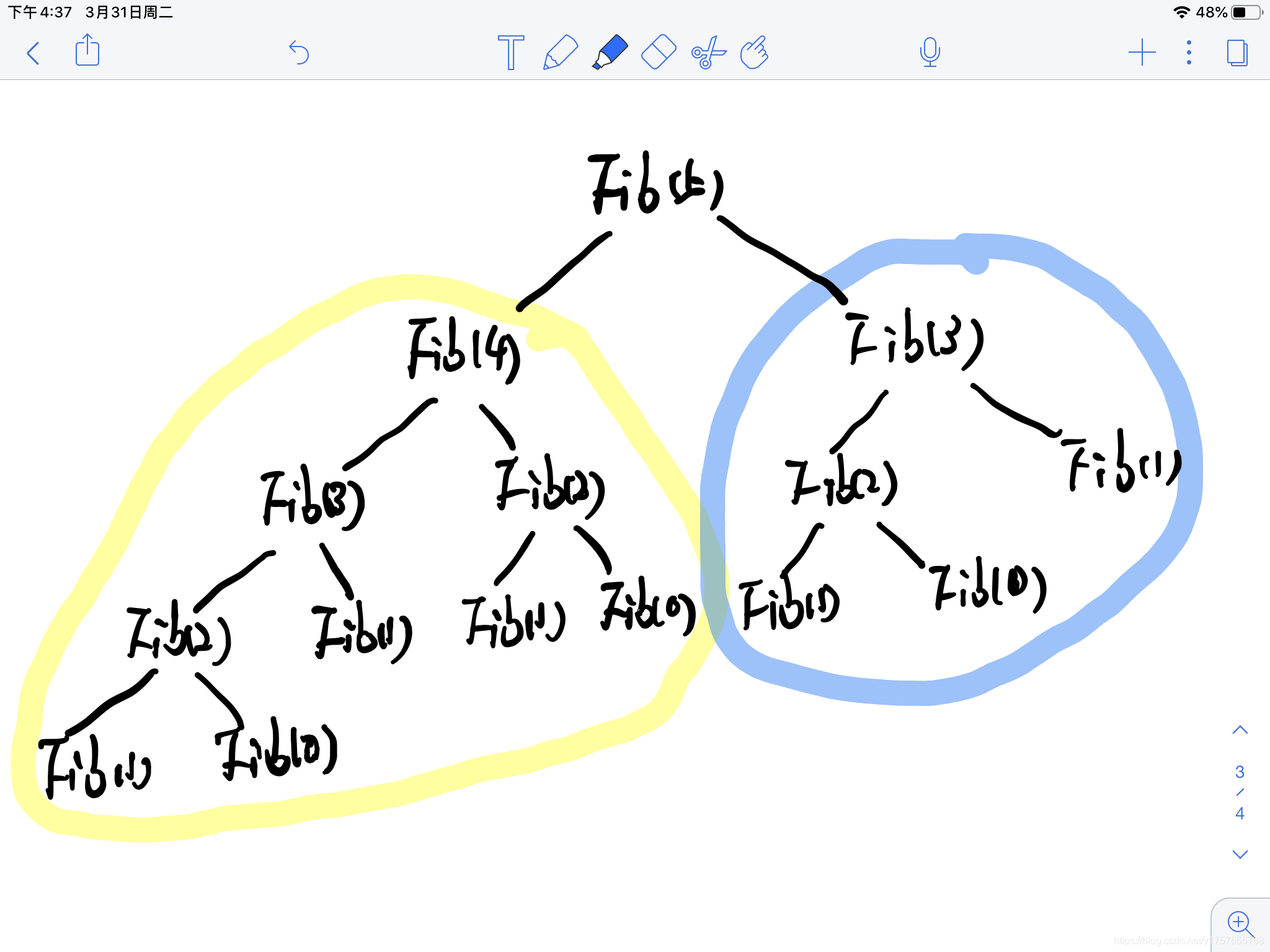
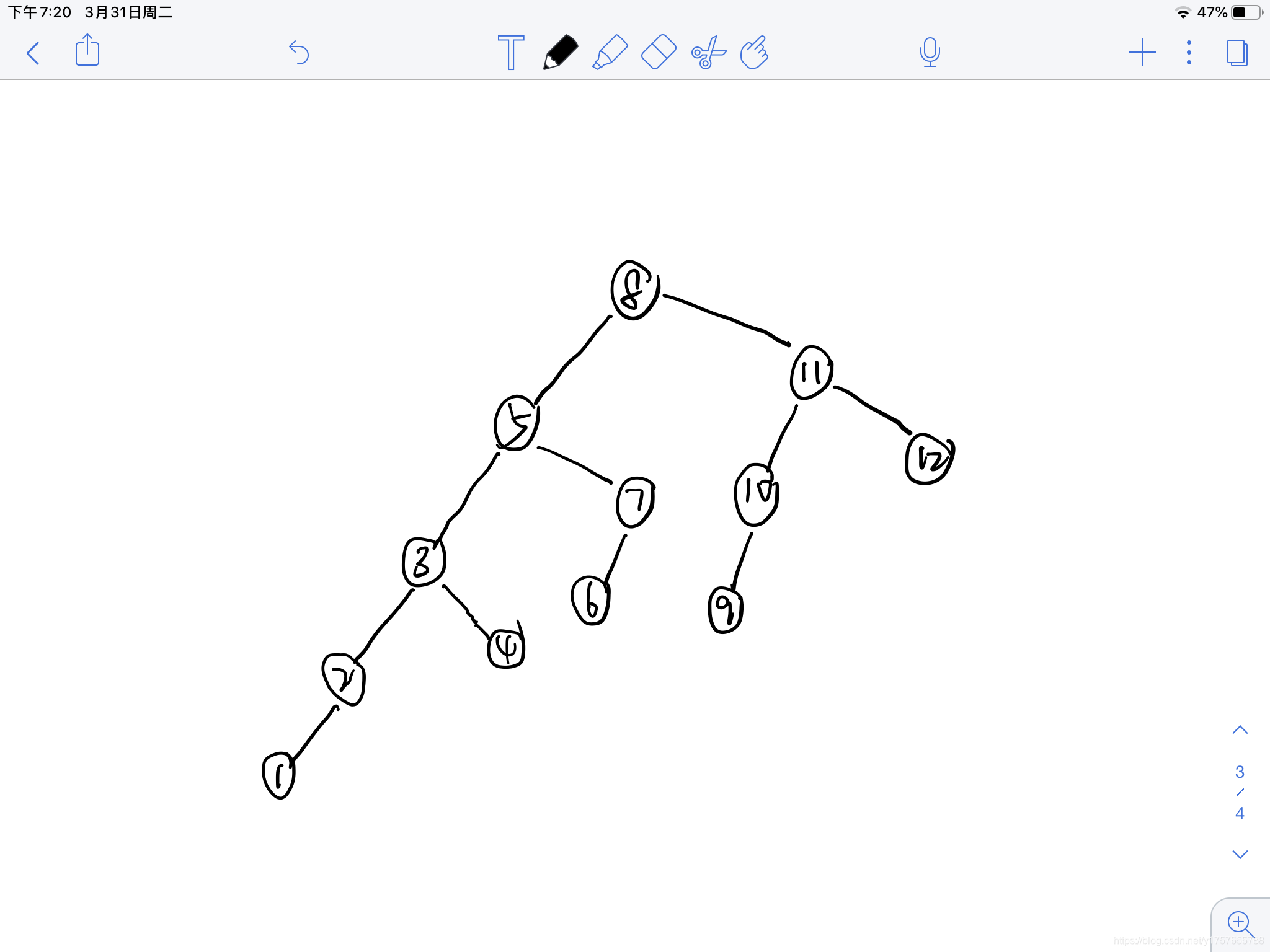
从这颗斐波那契树中可以大致看出来,左子树和右子树的结点数虽然不等,但是左子树的结点数永远不会超过右子树结点数的两倍,可以大致的看成是相对均匀的两部分,如果将数据以这个树形建成一颗搜索树,那么每颗子树根节点的序号就可以看成二分搜索的
m
i
d
mid
mid。
为什么要这么做?在对半查找中
m
i
d
=
(
l
o
w
+
h
i
g
h
)
/
2
mid=(low+high)/2
mid=(low+high)/2,这里
m
i
d
mid
mid的计算运用了除法,有些处理器中并没有浮点运算单元,像51单片机进行乘除运算就比较费资源。斐波那契查找正是极力想要避免查找过程中出现乘除运算,查找过程中
m
i
d
mid
mid的计算可以直接通过斐波那契数列得到,当表长为12(
f
7
−
1
f_7-1
f7−1)时,
m
i
d
=
8
mid=8
mid=8,即
m
i
d
mid
mid值为数列的前一个值。
既然斐波那契数列值是用来作为
m
i
d
mid
mid值,那么数列值应该是不重复的,否则会发生重复比较甚至出错,对于下列数列值中,1有重复,那么应该去掉一个,但是只去掉一个1,会导致整个数列不符合斐波那契公式,无法计算,所以去掉0和一个1,但是斐波那契的阶数保持不变。
| 阶数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | …… |
|---|---|---|---|---|---|---|---|---|
| 数列值 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | …… |
为了直观,建立一颗
1
1
1~
12
12
12的斐波那契树
1,2,3,5,8这条路径上确实满足斐波那契数列,可每颗子树的右子树并不满足。但是是有规律的,每颗右子树结点的值减去双亲结点的值却是满足斐波那契数列的。
为了简单,假设表长为12(
f
7
−
1
f_7-1
f7−1),为什么表长需要定义为
f
m
−
1
f_m-1
fm−1呢,这里跟二叉判定树是一样的,为了树形完整,便于运算分析。可以写出查找函数:
int search(s_list lst, int k, s_eletype* x)
{
int i = 1, p = 1, q = 2, t, n = lst.size;
while (q <= n) //见注释1
{
i = p;
p = q;
q = i + p;
}
i = p; //见注释2
p = q - i;
q = i - p;
for (;;)
{
if (k == lst.element[i-1].key)
{
*x = lst.element[i-1];
return true;
}
else
{
if (k < lst.element[i-1].key)
{
if (q == 0) return false;
else
{
i = i - q;
t = p;
p = q;
q = t - q;
}
}
else
{
if (p == 1)return false;
else
{
i = i + q;
p = p - q;
q = q - p;
}
}
}
}
}
注释1:计算斐波那契数列的最后三个数值:
i
=
f
m
−
2
i=f_{m-2}
i=fm−2,
p
=
f
m
−
1
p=f_{m-1}
p=fm−1,
q
=
f
m
q=f_m
q=fm。
注释2:颠倒
i
,
p
,
q
i,p,q
i,p,q,变成
i
=
f
m
−
1
i=f_{m-1}
i=fm−1,
p
=
f
m
−
2
p=f_{m-2}
p=fm−2,
q
=
f
m
−
3
q=f_{m-3}
q=fm−3。
p
,
q
p,q
p,q的大小永远往下减,代表的是以
i
i
i为根节点的子树所在阶数的斐波那契数列最高两位数列值。
因为斐波那契树不是一颗完全二叉树,所以将数据构建成的斐波那契数的高度会高于[lbn]+1,所以在最坏的情况下,斐波那契查找的时间性能不如对半查找;但是斐波那契的查找过程中没有乘除运算,所以在没有浮点运算单元的处理器中理论上平均性能会优于对半查找。
之所以说是理论上要比对半查找性能好,那是因为我们可以将对半查找的乘除运算转换为移位运算呀,乘2运算转换为左移一位,除2运算转换为右移一位,那平均性能妥妥的比斐波那契查找好。
本篇完 😉






















 1123
1123











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








