前言
如何较验一个算法的正确性，如何分析一个算法的好坏，以第一章“插入排序”为例子进行简单的介绍
插入排序
简单《简单插入排序》的“伪代码”如下
INSERTION-SORT[A]
for j ← 2 to length[A] // for 循环 j = 2, j < 数组A的length
key ← A[j] // A[j] 的值 给变量 key
i ← j-1 // i = j - 1
while i > 0 and A[i] >key // 内层循环
A[i+1] ← A[i]
i ← i-1
A[i+1] ← key
我们写出来一个算法，想要证明它是错的非常简单，只需要找到一组输入，如果算法得到了错误的输出，那么我们就可以确定的讲，这个算法是错的。那如何证明一个算法是否正确呢？
既然找到了一组错误的输入输出就可以证明算法是错的，那么我验证所有的输入输出，不就可以证明我的算法正确了吗？虽然这想法很容易想到，但恐怕没法实施，因为众所周知，自然数是无穷无尽的，等我们验证完所有的输入，那时候说不定《算法导论》已经成为幼儿园教材了。
我们或许也可以从数学归纳法的角度来进行思考：《循环不变式与算法的正确性》，其性质如下
- 初始化：循环的第一次迭代之前，它为真。
- 保持：如果循环的某次迭代之前它为真，那么下次迭代之前它仍为真。
- 终止：在循环终止时，不变式为我们提供了一个有用的性质，该性质有助于证明算法是正确的
以 [1, 22, 3, 4, 44, 55]数组输入为例子：
- 初始化，当j=2，数组[1],就1个元素，显然是正确的
- 保持，证明没一次循环都能让循环不变式成立，在外层循环中，让A[j-1], A[j-2],A[j-3]向右移动，找到A[j]的合适位置。
j=2 [1,22] j=3 [1,3,22] j=4 [1,3,4,22] j=5 [1,3,4,22,44] - 终止，在j>n时，循环结束了，把j替换为n+1,子数组A[1, n]包含了原来A[1,n]的元素，现在排序好了，他就是整个数组[1,3,4,22,44,55]，所以这是正确的。
练习
- 1-1手动模拟插入排序在数组A=[31,41,59,26,41,58]上的操作过
- 1-2重写插入排序使结果按降序排列
for j = 2 to A.length key = A[j] i = j - 1 while i > 0 and A[i] < key A[i + 1] = A[i] i = i - 1 A[i + 1] = key - 1-3要求对数组A=<a1,a2,...,an>实现线性查找代码,找不到返回NIL,并确保满足循环不变式的三个必要性质
SEARCH(A, v): for i = 1 to A.length if A[i] == v return i return NIL 1. 初始化：第一次迭代前i = 1 ， A为空，循环不变式显然成立。 2. 保持：假设第k-1次迭代前循环不等式成立，即A[1...k−1]中不存在值v。在第k次循环中，如果A[i]=v则算法结束，返回当前值的下标i（算“终止”，k-1 还是成立的）；如果A[i]≠v，则循环不变式成立。 3. 终止：中止有两种情况，找到v值返回下标i和没找到v值返回nil.
算法分析
分析算法的意味着预测算法需要的资源（内存,带宽,时间...),我们最想度量的是时间。在分析算法之前统一的实现技术模型，一般假定是通用单处理器计算模型——随机访问机(RAM)。
- 在RAM中，指令一条接一条执行，没有并发操作。
- RAM模型只能完成基本操作(常见指令),不能一条指令完成排序
- RAM模型中，每条指令所需要的时间都为常量
- RAM中的数据类型有整型和浮点型，我们大部分情况下不关注精度，除非某些特殊应用。
- 在真实的计算机中还包含一些特殊指令，我们尽量避免这些指令。例如计算2^𝑘，当k较小时，可以用移位来替换，我们当作常量时间计算。
- 我们在RAM模型中并不试图对内存层次进行建模(忽略高速缓存和虚拟内存)。有些情况下会考虑内存层次的影响，但是大部分情况下不会。
再以“插入排序” 为例子进行分析
插入排序算法需要的时间依赖于输入和被排序的程度。一般来说，算法的时间与输入的规模同步增长，所以通常把一个程序的运行时间描述成其输入规模的函数。
输入规模的概念依赖于研究的问题，如排序问题中，是输入的项数n.整数相乘时，是整数的位数。对于图，则使用顶点数和边数来描述。
一个算法在特定输入上的运行时间是指执行指令的操作次数。我们可以假定第𝑖行代码执行的时间为𝑐𝑖第i行代码执行的时间为ci; 如图所示，我们首先看看插入排序每条语句执行的次数和时间。(注：while/for 等循环退出时会多执行一次)
我们对运行时间求和，得到
当是最好情况下，即数组已经排好序时，可以观察到第6行，第七行不会被执行，第5行就可以看作普通式子，因此求和公式可更改为
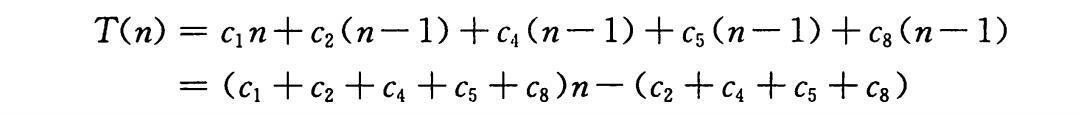
我们可以把该运行时间表示为𝑎𝑛+b，因此T(n)是n的线性函数；
当输入已经反向排序时，将导致最坏情况。我们必须将𝐴中的每个元素相比较（即第5，6，7三行打满），因此得到求和公式
我们可以把该运行时间表示为𝑎𝑛^2+bn+c,即T(n)为n的二次函数。
最坏情况与平均情况分析
上述分析出了插入排序的“最坏” 和 “最好” 时间。我们算法往往更集中于最坏情况运行时间分析，原因有三
- 最坏情况运行时间给出了上界，知道了这个上界就能确保算法绝不需要更长的时间。
- 对某些算法，最坏情况经常出现。
- 平均情况往往和最坏情况大致一样差
在某些特定情况下，我们会对算法的“平均”情况感兴趣，我们将看到概率分析技术被用于各种算法。平均情况分析范围有限，对于特定的问题，难以辨别什么才是平均情况。我们假设各种输入具有相同的可能性，实际上该假设可能并不成立。
增长量级
对于算法的时间分析，我们真正感兴趣的是运行时间的增长率或增长量级，因可以忽略执行的时间为ci;也忽略小项集，关注公式中最重要的项。
- “最好” 𝑎𝑛+b ，即 O(n)
- “最坏” 𝑎𝑛^2+bn+c 即 O(n^2)
练习
- 1-1用Θ 记号表示n^3/1000-100n^2-100n+3
O(n^3) - 2-2分析并实现《选择排序》算法,其偱环不变式，为什么循环中止于n-1,时间复杂度
SELECTION-SORT(A): 执行次数 // 终止于n-1 for i = 1 to A.length - 1 n-1 min = i n-1 for j = i + 1 to A.length n-1 + n-2 ... + 1 if A[j] < A[min] n-1 + n-2 ... + 1 min = j n-1 + n-2 ... + 1 temp = A[i] n-1 A[i] = A[min] n-1 A[min] = temp n-1 // 循环不变式 1.初始：子数组为空 2.保持：外层循环，子数组A[1..i]按升序排列 3.终止：当i=n-1时，子数组A[1...n]全部按升序排列 // 关于为什么循环到n-1 前n-1个元素是A中的从最小到第n-1小的元素排序好的，那么A[n]一定是最大的那个元素。 // 复杂度 最好情况（第五行不执行）： 5(n-1) + (n-1 + 1) (n-1) = (n-1)(n+5) 最坏情况 ：（n-1）(3n/2 + 5) 即为 O(n^2) - 2-3分析线性查找算法(练习1-3)，平均，最差。
因为待查找的元素是数组中任何一个元素的可能性是相等的，即都为1/n，则可得，平均情况下的查找次数为： (1+2+3+…+n)*(1/n) = (n-1)/2 最坏情况下可想而知是没有在该数列中找到对应的值，所以要遍历完整个数列才能确认，即n。 它们都是Θ(n)
设计算法
我们可以选择使用的算法设计技术有很多，插入排序使用了增量方法。我们也可以使用“分治法”的来设计一个排序算法。
分治法
分治策略是，把原问题划分为n个规模较小，结构与原问题相似的子问题。
递归解决子问题，然后合并结果得到原问题的解。
分治模式，在每一层递归上，都有3个步骤。
- 分解，把原问题划分为子问题。
- 解决，递归解决子问题，子问题足够小则直接解决。
- 合并，子问题的解合并为原问题的解。
归并排序算法完全遵循该模式，将n个元素分解为n/2个元素，使用归并排序递归解决子数列，合并已排序的子数列得到答案。
MERGE(A, p, q, r)
n1 = q-p+1
n2 = r-q
//let L[1....n1+1] and R[1....n2+1] be new arrays
for i =1 to n1
L[i] = A[p+i-1]
for j=1 to n2
R[j] = A[q+j]
L[n1+1] = ∞
L[n2+1] = ∞
i=1
j=1
for k =p to r
if L[i]<=R[j]
A[k] = L[i]
i = i + 1
else
A[k]=R[j]
j = j+1
MERGE-SORT(A,p,r)
if p < r
q =(p+r)/2 //向下取整，不会打那个符号
MERGE-SORT(A, p, q)
MERGE-SORT(A, q+1, r)
MERGE(A, p, q, r)归并排序的关键是，合并两个已排序好的子序列。通过一个 MERGE(A,p,q,r) 来实现 p <= q <= r 前提是子数组 A[p, q] 和 A[q+1, r] 是排序好的数组。通过合并这两个排序好的子数组来代替当前的子数组 A[p,r];
循环不变式:
- 初始化:在循环的第一次迭代之前，有𝑘=p,因此𝐴[𝑝..𝑘−1]为空，包含𝑘−𝑝=0个最小元素
- 保持：我们先假设𝐿[𝑖]<=𝑅[𝑗]，此时𝐿[𝑖]是未被复制回数组A的最小元素。因为A[p..k−1]包含k-p个最小元素，所以将𝐿[𝑖]复制到A[k]之后，子数组𝐴[𝑝..𝑘]A[p..k]将包含𝑘−𝑝+1k−p+1个最小元素，更新k值和i值后，即维持了原来的不等式成立。
- 终止:终止时𝑘=𝑟+1,根据循环不变式𝐴[𝑝..𝑘−1]就是A[p..r]且按照从小大大顺序包含L和R中的k-p个最小元素。
分析分治算法
我们可以用递归方程或递归式来描述递归分治算法的运行时间。分治算法运行时间的递归式来自于基本模式的三个步骤
- T(n)是规模为n的一个问题的运行时间。
- 当问题规模n<c(常量)时，则将运行时间写作Θ(1)。
- 否则，将原问题分解成𝑎个子问题，每个子问题的规模是原问题的1/b，求解𝑎个子问题就需要aT(n/b)的时间。分解成子问题需要时间D(n)，合并时间为C(n)
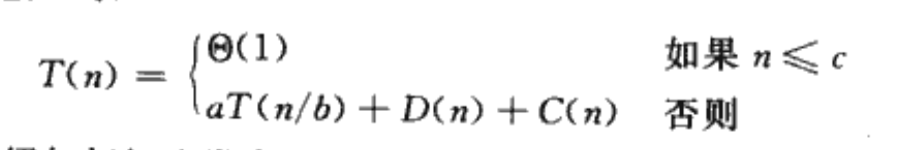
归并算法的分析
为了简化分析，假定原问题的规模是2的n次幂
- 分解：分解为规模为n/2的子问题，需要常量的时间，Θ(1)
- 解决 ：递归地求解两个规模为n/2的子问题，将贡献2T(n/2)的运行时间。
- 合并：合并需要Θ(n)的时间。
我们用常数c代表Θ(1),于是得到 T(n) = 2T(n/2) + cn，递归树总的层数是 lgn+1 ，每一层的代价是 cn，所以 T(n) = cn(lgn+1) => O(nlgn)
练习
- 3-1模拟A={3 41 52 26 38 57 9 49}归并排序操作
- 3-2重写归并排序，一量L或者R中元素都被复制回A后，立即停止将另一数组直接复制回A
MERGE(A, p, q, r) n1 = q - p + 1 n2 = r - q let L[1..n₁] and R[1..n₂] be new arrays for i = 1 to n₁ L[i] = A[p + i - 1] for j = 1 to n₂ R[j] = A[q + j] i = 1 j = 1 for k = p to r if i > n₁ A[k] = R[j] j = j + 1 else if j > n₂ A[k] = L[i] i = i + 1 else if L[i] ≤ R[j] A[k] = L[i] i = i + 1 else A[k] = R[j] j = j + 1 - 3-3使用数学归纳法证明: 当n=2的整次幂时，归并排序递归式
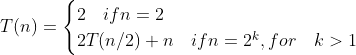的解是T(n)=nlgn
- 3-4更改插入排序为递归过程，并写出递归式
INSERTION-SORT(A, n) if n > 2 INSERTION-SORT(A, n-1) INSERTION(A, n) INSERTION(A, j) key = A[j] i = j - 1 while i > 0 and A[i] > key A[i+1] = A[i] i = i - 1 A[i+1] = key return // 递归式为 | n=1 0(1) T(n) = | | T(n-1) + C(n-1) -
3-5实现二分查找，并分析二分查找的最坏运行时间
BINARY-SEARCH(A, v): low = 1 high = A.length while low <= high mid = (low + high) / 2 if A[mid] == v return mid if A[mid] < v low = mid + 1 else high = mid - 1 return NIL // 最差时间 T(n+1)=T(n/2)+c => lgn -
3-6问插入排序与二分查找的结合是否能降低插入排序的时间复杂度
并不能，因为后面还有一个移动元素的逻辑，即使你找到了该插入的位置，但是移动的时候最坏的情况依然是 O(n^2)
思考题
- 2-1在归并排序中对小数组采用插入排序：归并排序最坏情况的运行时间为Θ(nlogn)，而插入排序最坏情况下为Θ(n^2)。但是插入排序中的常量因子可能使得它在n较小时在许多机器上运行更快。因此在归并排序中，当子问题变得足够小时采用插入排序来使得递归树的叶变粗是有意义的。该问题讨论了加入了插入排序的归并排序的算法复杂度以及选取在何时将归并操作代替为插排操作。
a. 证明：插入排序最坏情况可以在O(nk)时间内排序长度为k的n/k子表 插入排序最坏情况 = O(k^2)* n/k = O(nk) b. 表明在最坏吓如何在O(n lg(n/k))时间内合并这些子表 T(2a) = 2T(a) + k * 2a = 2(T(a)+ak) = 2(aklga + ak) = 2ak(lga+1)=2ak(lga+lg2)=2aklo2a=>nlg(n/k) c. 要让修定后最坏情况时间为：o(nk + nlg(n/k)) 和 标准最坏时间O(nlgn)一样,k的最大值 仅当k=lgn, O(nk + nlg(n/k)) = O(nlgn + nlg（n/lgn）) d. 在实践中，我们应该如何选择k 当插入排序优于归并排序时 -
2-2冒泡排序的正确性：利用循环不变式证明冒泡排序算法的正确性，并分析其算法复杂度。
BUBBLESORT(A) 1 for i=1 to A.length - 1 2 for j = A.length downto i + 1 3 if A[j] < A[j - 1] 4 exchange A[j] with A[j - 1] a. 假设A'表示BUBBLESORT的输出。为了证明BUBBLESORT正确，除了证明A'[1]<A'[2]<...<A'[n]，还要证明什么？ 证明 A'的元素和A是一样的 b/c. 是否符合循环不变式 初始：因为子数组为只有最后一个元素 保持：在每一步中，如果A[j]较小，我们用A[j−1]替换它。即A[j]>=A[j-1] 最终：最终i=j，子数组 = 数组 且按顺序排列 d. 冒泡排序最坏时间，及与插入排序的比较 运行时间是 O(n^2) .冒泡排序应该比插入排序更慢，因为交换意味着比插入排序更多的赋值 - 2-3霍纳规则的正确性：即多项式计算的秦九韵算法（简化多项式计算）。
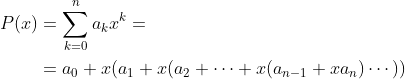
// 霍尔规则伪代码 y = 0 for i = n downto 0 y = aᵢ + x·y a. 上面代码运行时间 O(n) b. 朴素多项式伪代码，与霍尔规则性能相比 y = 0 for i = 0 to n m = 1 for k = 1 to i m = m·x y = y + aᵢ·m 即 O(n^2) c/d (略) -
2-4逆序对：计算逆序对个数，在排序算法中加入原数据的位置即可，逆序数在行列式的计算过程中也有一定提及。
a. 列出 i<j且A[i]>A[j] 的逆序对。A={2,3,8,6,1} 〈2,1〉, 〈3,1〉, 〈8,6〉, 〈8,1〉 , 〈6,1〉. b. 由集合{1,2,…,n} ，构成怎么样的数组，逆序对最多，具体多少对 A={n,n-1...2,1} (n-1 + 1)/2 * (n-1) 对 c. 插入排序运行时间和逆序对数量的什么关系 成正比，每一次交换都是在消灭逆序对， d. 求计算一数组A中逆序对算法，时间要求nlgn MERGE-SORT(A, p, r): if p < r inversions = 0 q = (p + r) / 2 inversions += merge_sort(A, p, q) inversions += merge_sort(A, q + 1, r) inversions += merge(A, p, q, r) return inversions else return 0 MERGE(A, p, q, r) n1 = q - p + 1 n2 = r - q let L[1..n₁] and R[1..n₂] be new arrays for i = 1 to n₁ L[i] = A[p + i - 1] for j = 1 to n₂ R[j] = A[q + j] i = 1 j = 1 for k = p to r if i > n₁ A[k] = R[j] j = j + 1 else if j > n₂ A[k] = L[i] i = i + 1 else if L[i] ≤ R[j] A[k] = L[i] i = i + 1 else A[k] = R[j] j = j + 1 inversions += n₁ - i return inversions
主要参考
《算法导论3rd》
561
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
