算法导论 — 思考题15-12 签约棒球自由球员

（签约棒球自由球员）假设你是一支棒球大联盟球队的总经理。在寒季休季期间，你需要签入一些自由球员。球队老板给你的预算为$X$美元，你可以使用少于$X$美元来签入球员。但如果超支，球队老板就会解雇你。
　　你正在考虑在$N$个不同位置签入球员，在每个位置上，有$P$个该位置的自由球员供你选择。由于你不希望任何位置过于臃肿，因此每个位置最多签入一名球员（如果在某个特定位置上你没有签入任何球员，则意味着计划继续使用现用球员）。
　　为了确定一名球员的价值，你决定使用一种称为“VORP”或称为“球员替换价值”(Value Over Replacement Player)的统计评价指标(sabermetric)。球员的VORP值越高，其价值越高。但VORP值高的球员的签约费用并不一定比VORP值低的球员高，因此还有球员价值之外的因素影响签约费用。
　　对每个可选择的自由球员，你知道他的三方面信息：
　　• 他打哪个位置
　　• 他的签约费用
　　• 他的VORP
　　设计一个球员选择算法，使得总签约费用不超过$X$美元，而球员的总VORP值最大。你可以假定每位球员的签约费用是10万美元的整数倍。算法应输出签约球员的总VORP值、总签约费用，以及球员名单。分析算法的时间和空间复杂度。
　　
　　解
　　本题要求预算为$X$美元的前提下签入$N$个不同位置的球员的最大化VORP值，用$v[N,X]$表示这个最大化VORP值。我们现在来提炼该问题的最优子结构。用$v[i,x]$表示预算为$x$美元$(0\le x\le X)$的前提下从$1$ ~ $i$个不同位置$(1\le i\le N)$签入球员的最大化VORP值。下面来建立$v[i,x]$的递归式。考虑第$i$个位置是否签入球员，分两种情况，用$v_1[i,x]$和$v_2[i,x]$分别表示两种情况下的最大化VORP值。
　　1) 第$i$个位置不签入球员
　　此时问题转化为预算仍然为$x$美元的前提下，从第$1$ ~ $i-1$个不同位置签入球员的最大化VORP值，即$v_1[i,x]=v[i-1,x]$。
　　2) 第$i$个位置签入一个球员
　　用$S_i[j]$表示第$i$个位置的第$j$个球员$(1\le j\le P)$。如果从第$i$个位置签入第$j$个球员，该球员的签约费用和VORP值分别为$S_i[j].cost$和$S_i[j].vorp$，那么剩下的资金为$x-S_i[j].cost$，我们接下来要用剩下的这些资金从$1$ ~ $i-1$个不同位置签入球员，即接下来要求解子问题$v[i-1,x-S_i[j].cost]$。此时总VORP值为$S_i[j].vorp+v[i-1,x-S_i[j].cost]$。当然，只有在满足$S_i[j].cost\le x$的条件下，才能从第$i$个位置签入第$j$个球员。由于每个位置最多只能签入一名球员，我们遍历从第$i$个位置签入任意一个球员的情况，从中选择总VORP值最大的情况。于是可以得到以下递归式。
　　
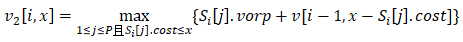
　　分别考察了情况1)和情况2)后，我们比较$v_1[i,x]$和$v_2[i,x]$，从中选择较大者。
　　我们还要特别考虑一下$i=1$的初始情况。此时，显然应当在预算范围内从第1个位置签入VORP值最大的球员。如果预算不足以签入第1个位置的任意一个球员，那么只能选择不签入球员。
　　综合以上分析，我们可以得到$v[i,x]$的递归式。
　　
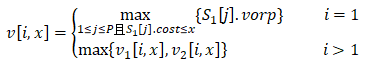
　　求解过程中，我们用一个数组$c[i,x]$表示在求解$v[i,x]$时从第$i$个位置选择签入了哪个球员。如果$c[i,x]=0$，表示在第$i$个位置没有签入球员。
　　
　　
　　该算法的核心是一个三重循环，很容易看出它的时间复杂度为$\Theta (NXP)$。