算法导论 — 4.4 用递归树方法求解递归式

笔记

在应用代入法求解递归式时，需要事先做出一个好的猜测。然而，有时候做出好的猜测是很困难的，此时可以考虑采用递归树方法。在递归树中，每个结点表示一个单一子问题的代价。创建递归树之后，对树的每层的各子问题的代价进行求和，得到每一层的代价，然后将所有层的代价加起来，得到整棵递归树的总代价，这个总代价就是递归式的解。当然，递归树方法是一种粗略的方法，因为递归树会引入一些“不精确”因素，这一点在后文再详细介绍。如果要精确求解递归式，还需要用代入法对递归树得到的解进行验证。
　　以递归式$T(n)=3T(\lfloor n/4\rfloor )+\Theta (n^2)$为例。为简化分析，我们将递归树中的$\Theta (n^2)$这一渐近符号项替换为一个代数式$c{n}^2$。这里引入了第一个“不精确”因素，但是我们认为这不会影响最终结果。于是我们将递归树变为$T(n)=3T(\lfloor n/4\rfloor )+c{n}^2$。为方便起见，我们还假定$n$是$4$的幂。这里又引入了一个“不精确”因素，但我们同样认为这不会影响最终结果。现在可以创建递归树，如下图所示。
　　
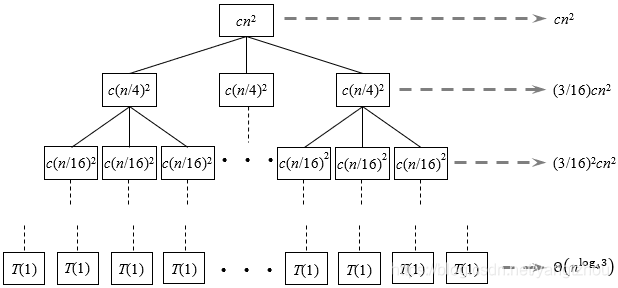
　　可以看到，递归树每下降一层，子问题规模减少为上一层的$1/4$，因此深度为$i$的结点，其子问题的规模为$n/4^i$。当到达叶结点时，子问题规模减为$1$。假设叶结点深度为$k$，那么有$n/4^k=1$，得到$k={\mathrm{l}\mathrm{o}\mathrm{g}}_{4}n$。所以叶结点深度为${\mathrm{l}\mathrm{o}\mathrm{g}}_{4}n$，这也说明整棵递归树的高度为${\mathrm{l}\mathrm{o}\mathrm{g}}_{4}n$。
　　现在统计递归树每一层的代价。对深度为$i$的非叶结点来说，每一个结点对应一个规模为$n/4^i$的子问题，每个子问题产生代价$c(n/4^i{)}^2=c{n}^2/16^i$。从递归树可以看到，递归树每下降一层，结点数目变为上一层的$3$倍，因此深度为$i$的结点一共有$3^i$个。于是可以得到，除叶结点那一层外，深度为$i$的那一层的结点代价之和为$3^i•(c{n}^2/16^i)=(3/16{)}^{i}c{n}^2$。
　　现在考虑叶结点。一个叶结点对应规模为$1$的子问题，它产生的代价为$T(1)$。通常来说，$T(1)$为常数时间，即$T(1)=\Theta (1)$。叶结点一共有$3^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}n}=n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}3}$个，所以叶结点那一层的代价为$n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}3}•T(1)=\Theta (n^{{\mathrm{l}\mathrm{o}\mathrm{g}}_{4}3})$。
　　现在将递归树每一层代价加起来，得到递归树的总代价为
　　
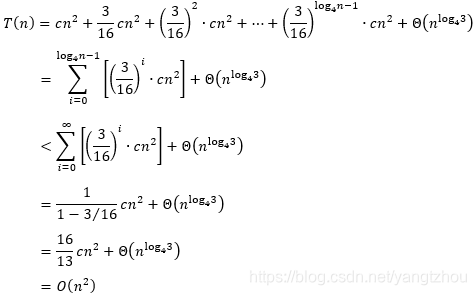
　　这样，对原始递归式$T(n)=3T(\lfloor n/4\rfloor )+\Theta (n^2)$，我们得到了一个猜测解$T(n)=O(n^2)$。由于根结点对总代价的贡献为$c{n}^2$，所以根结点的代价支配了整棵递归树的总代价。
　　现在用代入法对猜测解进行验证。我们要证明的是：存在正常数$d$，使得$T(n)\le d{n}^2$对足够大的$n$都成立。将$T(n)\le d{n}^2$代入递归式得到
　　
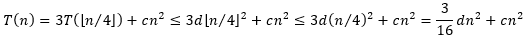
　　当$d\ge \frac{16}{13}c$时，不等式$\frac{3}{16}d{n}^2+c{n}^2\le d{n}^2$成立，此时$T(n)\le d{n}^2$成立。因此$T(n)=O(n^2)$得证。
　　现在考察一个更复杂的递归式$T(n)=T(n/3)+T(2n/3)+O(n)$。与之前一样，将渐近项$O(n)$替换为代数式$cn$，递归式变为$T(n)=T(n/3)+T(2n/3)+cn$。现在创建递归树，如下图所示。
　　
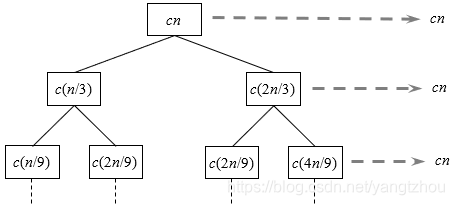
　　由于每个结点的左右孩子的规模不一样，这意味着每个结点的左右子树的高度不一样，右子树比左子树要高，因此这棵树并不是一棵满二叉树。从根结点到叶结点的最长简单路径是$n\to (2/3)n\to (2/3{)}^{2}n\to \dots \to 1$。假设树的高度为$h$，那么有$(2/3{)}^h•n=1$，得到$h={\mathrm{l}\mathrm{o}\mathrm{g}}_{3/2}n$。
　　在上图中，我们只画出了递归树的顶部几层，可以看到每层的代价都为$cn$。然而由于递归树并不是一棵满二叉树，所以并不是每层的代价都为$cn$。随着递归树的层级越往下降，缺失的结点会越来多，这些存在缺失结点的层级的代价小于$cn$。只有递归树靠顶部的那些不存在缺失结点的层级，它们的代价等于$cn$。由于我们只需要通过递归树获得一个猜测解，所以我们不考虑这些缺失结点的影响，于是我们猜测解为$T(n)=O(cn•{\mathrm{l}\mathrm{o}\mathrm{g}}_{3/2}n)=O(n\mathrm{l}\mathrm{g}n)$。注意，这里又引入了另一种形式的“不精确”因素。
　　现在用代入法对猜测解进行验证。我们要证明的是：存在正常数$d$，使得$T(n)\le dn\mathrm{l}\mathrm{g}n$对足够大的$n$都成立。将$T(n)\le dn\mathrm{l}\mathrm{g}n$代入递归式得到
　　
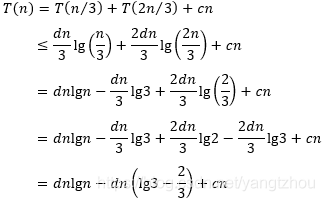
　　只要取$d\ge \frac{c}{\mathrm{l}\mathrm{g}3-2/3}$，就能使得不等式$dn\mathrm{l}\mathrm{g}n-dn(\mathrm{l}\mathrm{g}3-\frac{2}{3})+cn\le dn\mathrm{l}\mathrm{g}n$成立，此时$T(n)\le dn\mathrm{l}\mathrm{g}n$成立。因此$T(n)=O(n\mathrm{l}\mathrm{g}n)$得证。

练习

4.4-1 对递归式$T(n)=3T(\lfloor n/2\rfloor )+n$，利用递归树确定一个好的渐近上界，用代入法进行验证。
　　解
　　创建递归树，如下图所示。
　　
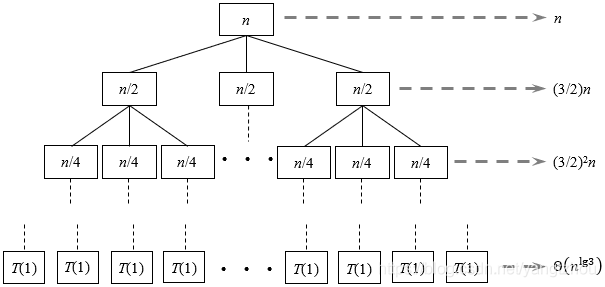
　　在递归树中，深度为$i$的结点对应规模为$n/2^i$的子问题。当$n/2^i=1$时，即$i=\mathrm{l}\mathrm{g}n$时，子问题规模变为$1$，这对应于叶结点$T(1)$，因此树的高度$h=\mathrm{l}\mathrm{g}n$。
　　每层的结点数都是上一层的$3$倍，因此深度为$i$的结点数为$3^i$。深度为$i$的结点对应的子问题规模为$n/2^i$，除叶结点外，深度为$i$的每个结点的代价为$n/2^i$。因此，除叶结点外，深度为$i$的所有结点的代价为$3^i•(n/2^i)=(3/2{)}^{i}n$。叶结点一共有$3^{\mathrm{l}\mathrm{g}n}=n^{\mathrm{l}\mathrm{g}3}$个，所以叶结点那一层的代价为$\Theta (n^{\mathrm{l}\mathrm{g}3})$。
　　现在将每一层的代价加起来，得到
　　
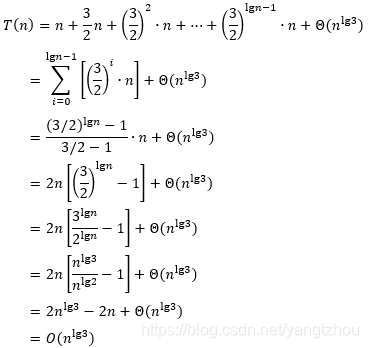
　　下面用代入法验证这一结果。在做归纳假设时，需要减去一个低阶项，才能顺利完成证明。于是我们要证明的是：存在正常数$c$和$d$，使得$T(n)\le c{n}^{\mathrm{l}\mathrm{g}3}-dn$对足够大的n都成立。
　　取初始情况$T(1)=1$。只要取$c\ge d+1$，就能使得$T(1)\le c•1^{\mathrm{l}\mathrm{g}3}-d•1=c-d$成立。
　　现在考虑$n\ge 2$的情况。假设$T(n)\le c{n}^{\mathrm{l}\mathrm{g}3}-dn$对$1,2,\dots ,n-1$都成立，于是有
　　$T(n)=3T(\lfloor n/2\rfloor )+n\le 3c(\frac{n}{2}{)}^{\mathrm{l}\mathrm{g}3}-3d•\frac{n}{2}+n=c{n}^{\mathrm{l}\mathrm{g}3}-(\frac{3}{2}d-1)n$
　　现在要选取合适的$c$和$d$，使得不等式$c{n}^{\mathrm{l}\mathrm{g}3}-(\frac{3}{2}d-1)n\le c{n}^{\mathrm{l}\mathrm{g}3}-dn$成立。对该不等式做一下变换。
　　$c{n}^{\mathrm{l}\mathrm{g}3}-(\frac{3}{2}d-1)n\le c{n}^{\mathrm{l}\mathrm{g}3}-dn$　　⇔　　$(\frac{3}{2}d-1)n\ge dn$　　⇔　　$d\ge 2$
　　因此，只要取$d\ge 2$，并且$c$取任意值，就能使能不等式$c{n}^{\mathrm{l}\mathrm{g}3}-(\frac{3}{2}d-1)n\le c{n}^{\mathrm{l}\mathrm{g}3}-dn$成立，此时$T(n)\le c{n}^{\mathrm{l}\mathrm{g}3}-dn$成立。
　　综合考虑初始情况$T(1)$，我们最终要取$d\ge 2$并且$c\ge d+1$。于是$T(n)=O(n^{\mathrm{l}\mathrm{g}3})$得证。

4.4-2 对递归式$T(n)=T(n/2)+n^2$，利用递归树确定一个好的渐近上界，用代入法进行验证。
　　解
　　创建递归树，如下图所示。　　
　　
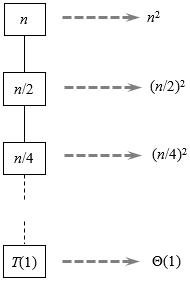
　　在递归树中，深度为$i$的结点对应规模为$n/2^i$的子问题。当$n/2^i=1$时，即$i=\mathrm{l}\mathrm{g}n$时，子问题规模变为$1$，这对应于叶结点$T(1)$，因此树的高度$h=\mathrm{l}\mathrm{g}n$。
　　每层只有一个结点。除叶结点外，深度为$i$的结点的代价为$(n/2^i{)}^2=n^2/4^i$。叶结点的代价为$T(1)=\Theta (1)$。现在将每一层的代价加起来，得到
　　
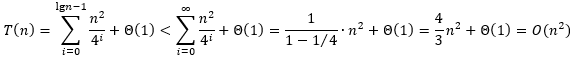
　　用代入法验证这一结果比较简单，这里省略具体过程。
　　
4.4-3 对递归式$T(n)=4T(n/2+2)+n$，利用递归树确定一个好的渐近上界，用代入法进行验证。
　　解
　　直接对递归式$T(n)=4T(n/2+2)+n$创建递归树很困难。将递归式变换为$T(n)=4T(n/2)+n$，因为当$n$足够大时$n/2+2$和$n/2$很接近，我们预计这样做不会影响最终结果。现在创建递归树，如下图所示。
　　
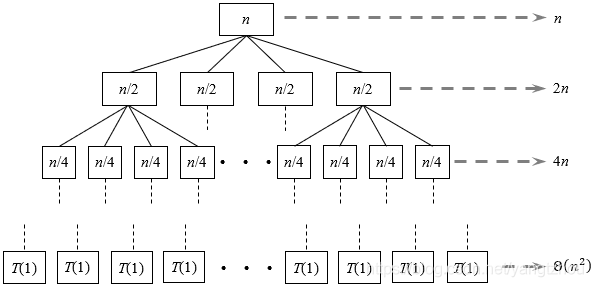
　　在递归树中，深度为$i$的结点对应规模为$n/2^i$的子问题。当$n/2^i=1$时，即$i=\mathrm{l}\mathrm{g}n$时，子问题规模变为$1$，这对应于叶结点$T(1)$，因此树的高度$h=\mathrm{l}\mathrm{g}n$。
　　每层的结点数都是上一层的$4$倍，因此深度为$i$的结点数为$4^i$。深度为$i$的结点对应的子问题规模为$n/2^i$，除叶结点外，深度为$i$的每个结点的代价为$n/2^i$。因此，除叶结点外，深度为$i$的所有结点的代价为$4^i•(n/2^i)=2^i•n$。叶结点一共有$4^{\mathrm{l}\mathrm{g}n}=n^2$个，所以叶结点那一层的代价为$\Theta (n^2)$。
　　现在将每一层的代价加起来，得到
　　
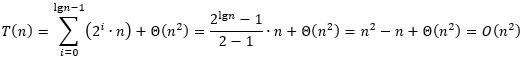
　　下面用代入法验证这一结果。我们没有办法直接证明$T(n)\le c{n}^2$，不妨证明：存在正常数$c$和$d$，使得$T(n)\le c(n-4{)}^2-d(n-4)$对足够大的$n$都成立。
　　要使原递归式$T(n)=4T(n/2+2)+n$有意义，必须有$n>n/2+2$，得到$n>4$，即$n\ge 5$。所以取初始情况$T(5)=1$。只要取$c\ge d+1$，就能使得$T(5)\le c•(5-4{)}^2-d•(5-4)=c-d$成立。
　　现在考虑$n\ge 6$的情况。假设$T(n)\le c(n-4{)}^2-d(n-4)$对$5,6,\dots ,n-1$都成立，于是有
　　
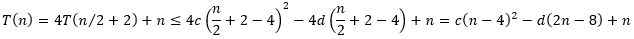
　　现在要选取合适的$c$和$d$，使得不等式$c(n-4{)}^2-d(2n-8)+n\le c(n-4{)}^2-d(n-4)$成立。对这个不等式做一下变换。
　　
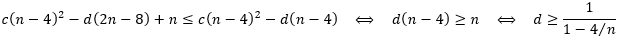
　　当$n\ge 6$时，$1/(1-4/n)$是单调递减的，并且在$n=6$时取得最大值为$3$。因此，只要取$d\ge 3$，就能使得不等式$c(n-4{)}^2-d(2n-8)+n\le c(n-4{)}^2-d(n-4)$成立，此时$T(n)\le c(n-4{)}^2-d(n-4)$成立。
　　综合考虑初始情况$T(5)$，我们最终要取$d\ge 3$并且$c\ge d+1$。于是$T(n)=O(n^2)$得证。

4.4-4 对递归式$T(n)=2T(n-1)+1$，利用递归树确定一个好的渐近上界，用代入法进行验证。
　　解
　　创建递归树，如下图所示。
　　
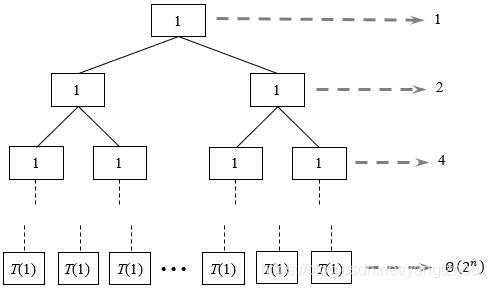
　　在递归树中，深度为$i$的结点对应规模为$n-i$的子问题。当$n-i=1$时，即$i=n-1$时，子问题规模变为$1$，这对应于叶结点$T(1)$，因此树的高度$h=n-1$。
　　每层的结点数都是上一层的$2$倍，因此深度为$i$的结点数为$2^i$。除叶结点外，每个结点的代价都为$1$。因此，除叶结点外，深度为i的所有结点的代价为$2^i•1=2^i$。叶结点一共有$2^{n-1}$个，所以叶结点那一层的代价为$\Theta (2^n)$。
　　现在将每一层的代价加起来，得到
　　
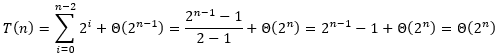
　　下面用代入法验证这一结果。在做归纳假设时，需要减去一个低阶项，才能顺利完成证明。我们要证明的是：存在正常数$c$和$d$，使得$T(n)\le c•2^n-d$对足够大的$n$都成立。
　　取初始情况$T(1)=1$。只要取$c\ge (d+1)/2$，就能使得$T(1)\le c•2^1–d=2c–d$成立。
　　现在考虑$n\ge 2$的情况。假设$T(n)\le c•2^n-d$对$1,2,\dots ,n-1$都成立，于是有
　　$T(n)=2T(n-1)+1\le 2c•2^{n-1}-2d+1=c•2^n-2d+1$
　　只要取$d\ge 1$，就能使得$c•2^n-2d+1\le c•2^n-d$成立，此时$T(n)\le c•2^n-d$成立。
　　综合考虑初始情况$T(1)$，我们最终要取$d\ge 1$并且$c\ge (d+1)/2$。于是$T(n)=O(2^n)$得证。

4.4-5 对递归式$T(n)=T(n-1)+T(n/2)+n$，利用递归树确定一个好的渐近上界，用代入法进行验证。
　　解
　　创建递归树，如下图所示。
　　
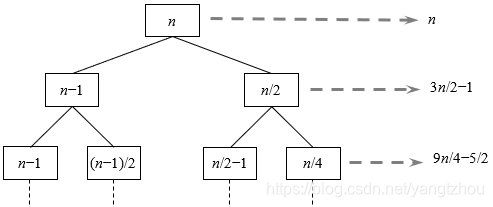
　　该递归树显然不是一棵满二叉树。从根结点到叶结点的最短简单路径是$n\to n/2\to n/4\to \dots \to 1$。假设这一最短简单路径上叶结点深度为$k$，那么有$(1/2)k•n=1$，得到$k=\mathrm{l}\mathrm{g}n$。从根结点到叶结点的最短简单路径是$n\to n-1\to n-2\to \dots \to 1$。假设这一最短简单路径上叶结点深度为$l$，那么有$n-l=1$，得到$l=n-1$。
　　从递归树可以看到，第i层的代价为$(3/2{)}^i•n–e$，其中$e$为低阶项。我们要确定$T(n)$的渐近上界，为方便起见，忽略每一层代价中的低阶项$e$，统计第$0$层到第$n-1$层的代价之和，得到
　　
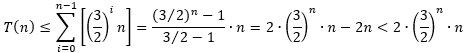
　　当$n$足够大时，有$2•(3/2{)}^n•n<2^n$，因此得到$T(n)=O(2^n)$。
　　下面用代入法验证这一结果。在做归纳假设时，需要减去一个低阶项，才能顺利完成证明。我们要证明的是：存在正常数$c$和$d$，使得$T(n)\le c•2^n-dn$对足够大的n都成立。
　　取初始情况$T(1)=1$。只要取$c\ge (d+1)/2$，就能使得$T(1)\le c•2^1–d•1=2c–d$成立。
　　现在考虑$n\ge 2$的情况。假设$T(n)\le c•2^n-dn$对$1,2,\dots ,n-1$都成立，于是有
　　
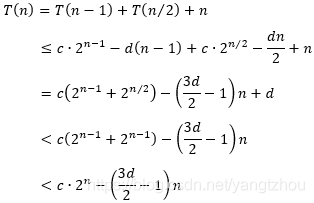
　　现在要选取合适的$c$和$d$，使得不等式$c•2^n-(\frac{3d}{2}-1)n\le c•2^n-dn$成立。对该不等式做一下变换。
　　
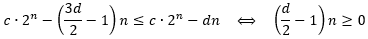
　　显然，只要取$d\ge 2$，就能使得$c•2^n-(\frac{3d}{2}-1)n\le c•2^n-dn$成立，此时$T(n)\le c•2^n-dn$成立。
　　综合考虑初始情况$T(1)$，我们最终要取$d\ge 2$并且$c\ge (d+1)/2$。于是$T(n)=O(2^n)$得证。

4.4-6 对递归式$T(n)=T(n/3)+T(2n/3)+cn$，利用递归树论证其解为$\Omega (n\mathrm{l}\mathrm{g}n)$，其中$c$为常数。
　　解
　　创建递归树，如下图所示。
　　
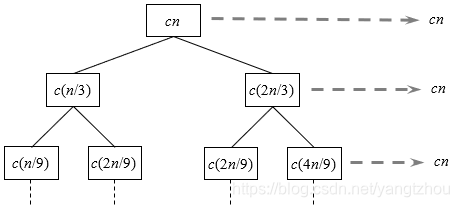
　　由于每个结点的左右孩子的规模不一样，这意味着每个结的左右子树的高度不一样，右子树比左子树要高，因此这棵树并不是一棵满二叉树。从根结点到叶结点的最短简单路径是$n\to (1/3)n\to (1/3{)}^{2}n\to \dots \to 1$。假设这一最短简单路径上叶结点深度为$k$，那么有$(1/3{)}^k•n=1$，得到$k={\mathrm{l}\mathrm{o}\mathrm{g}}_{3}n$。这意味着递归树中第${\mathrm{l}\mathrm{o}\mathrm{g}}_{3}n$层及以上的层级都是满的，这些层级的每一层的代价都为$cn$。
　　我们求的是$T(n)$的渐近下界，因此可以只统计递归树中第${\mathrm{l}\mathrm{o}\mathrm{g}}_{3}n$层及以上的层级的代价。于是得到
　　
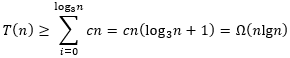
　　用代入法验证这一结果比较简单，这里省略具体过程。

4.4-7 对递归式$T(n)=4T(\lfloor n/2\rfloor )+cn$（$c$为常数），画出递归树，并给出其解的一个渐近紧确界。用代入法进行验证。
　　解
　　本题的递归树与练习4.4-3的递归树几乎一样，如下图所示。
　　
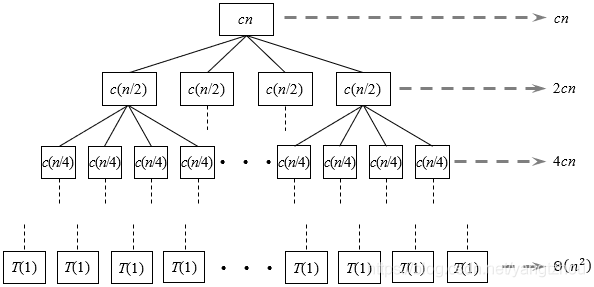
　　将每一层的代价加起来，得到
　　
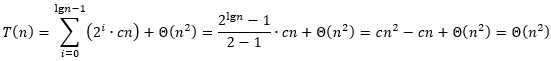
　　下面用代入法验证这一结果。在做归纳假设时，需要减去一个低阶项，才能顺利完成证明。于是我们要证明的是：存在正常数$d_1$、$d_2$和$e$，使得$d_1(n^2-en)\le T(n)\le d_2(n^2-en)$对足够大的$n$都成立。需要分两步证明。
　　(1) 证明存在正常数$d_1$和$e$，使得$T(n)\ge d_1(n^2-en)$对足够大的n都成立
　　取初始情况$T(1)=1$。只要取$d_1\le 1/(1-e)$并且$e<1$，就能使得$T(1)\ge d_1(1^2-e•1)=d_1(1-e)$成立。
　　现在考虑$n\ge 2$的情况。假设$T(n)\ge d_1(n^2-en)$对$1,2,\dots ,n-1$都成立，于是有
　　
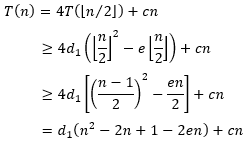
　　现在要选取合适的$d_1$和$e$，使得不等式$d_1(n^2-2n+1-2en)+cn\ge d_1(n^2-en)$成立。对该不等式做一下变换。
　　
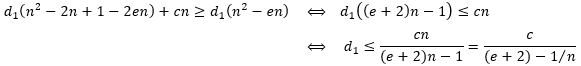
　　当$n\ge 2$时，$\frac{c}{(e+2)-1/n}$是单调递减的，并且在$n=\infty$时取得最小值为$\frac{c}{e+2}$。因此，只要取$d_1\le \frac{c}{e+2}$，就能使得不等式$d_1(n^2-2n+1-2en)+cn\ge d_1(n^2-en)$成立，此时$T(n)\ge d_1(n^2-en)$成立。
　　综合考虑初始情况$T(1)$，我们最终要取$e<1$并且 d 1 ≤ m i n { 1 1 − e , c e + 2 } d_1 ≤ min\{\frac{1}{1−e}, \frac{c}{e+2}\} d1​≤min{1−e1​,e+2c​}。于是$T(n)\ge d_1(n^2-en)$得证。
　　(2) 证明存在正常数$d_2$和$e$，使得$T(n)\le d_2(n^2-en)$对足够大的$n$都成立
　　取初始情况$T(1)=1$。只要取$d_2\ge 1/(1-e)$并且$e<1$，就能使得$T(1)\le d_2(1^2-e•1)=d_2(1-e)$成立。
　　现在考虑$n\ge 2$的情况。假设$T(n)\le d_2(n^2-en)$对$1,2,\dots ,n-1$都成立，于是有
　　
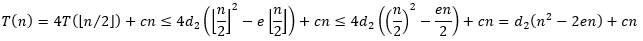
　　现在要选取合适的$d_2$和$e$，使得不等式$d_2(n^2-2en)+cn\le d_2(n^2-en)$成立。对该不等式做一下变换。
　　
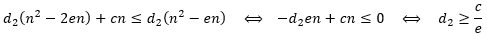
　　因此，只要取$d_2\ge c/e$，就能使能不等式$d_2(n^2-2en)+cn\le d_2(n^2-en)$成立，此时$T(n)\le d_2(n^2-en)$成立。
　　综合考虑初始情况$T(1)$，我们最终要取$e<1$并且 d 2 ≤ m a x { 1 1 − e , c e } d_2 ≤ max\{\frac{1}{1−e}, \frac{c}{e}\} d2​≤max{1−e1​,ec​}。于是$T(n)\le d_2(n^2-en)$得证。
　　综合(1)和(2)，只要取$e<1$、 d 1 ≤ m i n { 1 1 − e , c e + 2 } d_1 ≤ min\{\frac{1}{1−e}, \frac{c}{e+2}\} d1​≤min{1−e1​,e+2c​}并且 d 2 ≤ m a x { 1 1 − e , c e } d_2 ≤ max\{\frac{1}{1−e}, \frac{c}{e}\} d2​≤max{1−e1​,ec​}，就能使得$d_1(n^2-en)\le T(n)\le d_2(n^2-en)$成立。因此，$T(n)=\Theta (n^2)$得证。

4.4-8 对递归式$T(n)=T(n-a)+T(a)+cn$，利用递归树给出一个渐近紧确解，其中$a\ge 1$和$c>0$是常数。
　　解
　　创建递归树，如下图所示。
　　
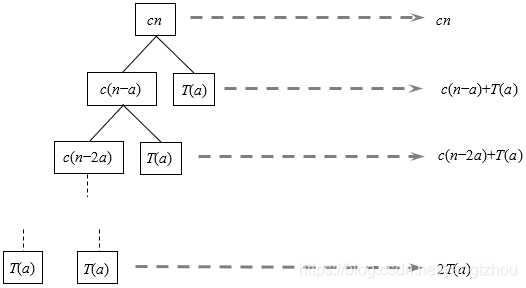
　　在递归树中，每个结点均有$2$个孩子，其中右孩子都为$T(a)$。所以除根结点外，每一层都只有$2$个结点。深度为$i$的结点其中一个对应规模为$n-ai$的子问题，另一个对应规模为$a$的子问题。当$n-ai=a$时，即$i=(n/a)-1$时，子问题规模变为$a$，这对应于最底层的叶结点$T(a)$，因此树的高度$h=(n/a)-1$。
　　除叶结点外，深度为$i$的结点其中一个对应规模为$n-ai$的子问题，它的代价为$c(n-ai)$；另一个对应规模为$a$的子问题，它的代价为$T(a)$。因此，除叶结点外，深度为$i$的所有结点的代价为$c(n-ai)+T(a)$。叶结点一共有$2$个，所以叶结点那一层的代价为$2T(a)$。
　　现在将每一层的代价加起来，得到
　　
　　
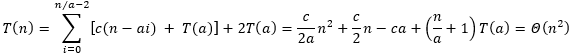
4.4-9 对递归式$T(n)=T(\alpha n)+T((1-\alpha )n)+cn$，利用递归树给出一个渐近紧确解，其中$0<\alpha <1$和$c>0$是常数。
　　解
　　创建递归树，如下图所示。
　　
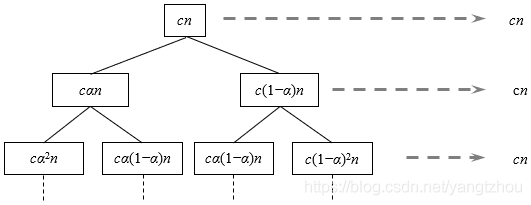
　　为方便起见，假设$0<\alpha \le 1/2$。$1/2<\alpha <1$是对称的情况。从根结点到叶结点的最短简单路径是$n\to \alpha n\to \alpha 2n\to \dots \to 1$。假设这一最短简单路径上叶结点深度为$k$，那么有${\alpha }^k•n=1$，得到$k={\mathrm{l}\mathrm{o}\mathrm{g}}_{1/\alpha }n$。从根结点到叶结点的最短简单路径是$n\to (1-\alpha )n\to (1-\alpha )2n\to \dots \to 1$。假设这一最短简单路径上叶结点深度为$l$，那么有$(1-\alpha {)}^l•n=1$，得到$l={\mathrm{l}\mathrm{o}\mathrm{g}}_{1/(1-\alpha )}n$。
　　上图画出了递归树的顶部几层，顶部几层的代价都等于$cn$，严格来说，从根结点到第${\mathrm{l}\mathrm{o}\mathrm{g}}_{1/\alpha }n$层，每一层的代价都为$cn$。只统计根结点到第${\mathrm{l}\mathrm{o}\mathrm{g}}_{1/\alpha }n$层的代价，就可以得到$T(n)$的下界，于是有
　　
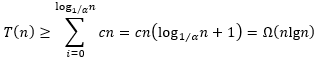
　　随着递归树层级往下降，缺失的内部结点越来越多，因此底部几层的代价都不超过$cn$。于是有
　　
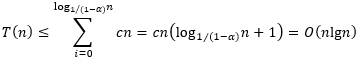
　　综合以上分析，得到$T(n)=\Theta (n\mathrm{l}\mathrm{g}n)$。