数据预处理——插值算法matlab实现

最新推荐文章于 2025-03-12 12:51:25 发布

yanyanwenmeng

最新推荐文章于 2025-03-12 12:51:25 发布

阅读量1w

点赞数 16

分类专栏：数学建模 matlab

本文链接：https://blog.csdn.net/yanyanwenmeng/article/details/109992809

版权

数学建模同时被 2 个专栏收录

35 篇文章

订阅专栏

matlab

8 篇文章

订阅专栏

本文详细介绍了插值算法在数学建模中的应用，包括一维插值问题、分段线性插值、拉格朗日与牛顿插值、埃尔米特插值以及三次样条插值。通过对不同插值方法的原理和实现的讲解，展示了它们在数据预处理和短期预测中的作用。以实例展示了如何使用分段三次埃尔米特插值和三次样条插值来补充缺失数据，并比较了两者的效果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

笔记来自《清风数学建模》系列课程课程链接

（2）分段三次埃尔米特插值编程实现（建模比赛中最常用）

4. 三次样条插值

（1）原理

（2）三次样条插值编程实现（建模中最常用）

3. 三次样条插值和三次埃尔米特插值的对比

一、插值算法的用途

数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满足需求，这就是插值的作用。

二、一维插值问题

限制多项式的次数，插值的函数是唯一的。但是插值多项式次数越高误差越小吗？

红色的为标准正确的函数图像。后面是不同插值次数的图像。可以发现，高次插值会产生龙格现象，即在两端处波动极大,产生明显的震荡。在不熟悉曲线运动趋势的前提下，不要轻易使用高次插值。

由于插值多项式的次数高但是精度未必高，相反，次数越高可能产生的误差越大。为了减少这种误差，我们可以使用分段线性插值。

三、分段线性插值

1.简单分段线性插值

如何提高插值的精度呢？我们可以采用分段线性插值。比如要得到C点的y值，可以得到A、B两点构成的线段的函数关系式，通过函数关系式求得C点的y值。线性是值找离它最近的两个点求得线性函数进行求解。

也可以选择离C点最近的3个点计算得到抛物线的函数关系式从而进行求解。这种就叫分段二次插值（实际建模时用的比较多）。

2. 拉格朗日插值与牛顿插值

上述两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值，而这种插值多项式却不能全面反映被插值函数的性态。然而在许多实际问题中，不仅要求插值函数与被插值函数在所有节点处有相同的函数值，它也需要在一个或全部节点上插值多项式与被插函数有相同的低阶甚至高阶的导数值。对于这些情况，拉格朗日插值和牛顿插值都不能满足。

3. 埃尔米特 (Hermite)插值

（1）原理

不但要求在节点上的函数值相等，而且还要求对应的导数值也相等,甚至要求高阶导数也相等，满足这种要求的插值多项式就是埃尔米特插值多项式。（保证函数和导数相等）

（2）分段三次埃尔米特插值编程实现（建模比赛中最常用）

直接使用Hermite插值得到的多项式次数较高，也存在着龙格现象，因此在实际应用中，往往使用分段三次 Hermite 插值多项式 (PCHIP)。

Matlab有内置的函数（实现过程已经帮我们封装好了，会调用就行了）：

p = pchip(x,y, new_x)

x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

% 分段三次埃尔米特插值
x = -pi:pi;%题目中给定的x值步长为1
y = sin(x); 
new_x = -pi:0.1:pi;%需要插值的x值步长为0.1
p = pchip(x,y,new_x);
plot(x, y, 'o', new_x, p, 'r-')

plot函数用法:
plot(x1,y1,x2,y2)
线方式： ‐ 实线 :点线 ‐. 虚点线 ‐ ‐ 波折线
点方式： . 圆点 +加号 * 星号 x x形 o 小圆
颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青

4. 三次样条插值

（1）原理

（2）三次样条插值编程实现（建模中最常用）

Matlab有内置的函数：

p = spline (x,y, new_x)

x是已知的样本点的横坐标;y是已知的样本点的纵坐标;new_x是要插入处对应的横坐标

% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x);   %分段三次埃尔米特插值
p2 = spline(x,y,new_x);  %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')   %标注显示在东南方向

【分析】通过图发现，在这个例子中，三次样条插值的图像更为光滑，精确度要更高一些，更加接近于sin(x)这个原始函数。

可以看出，三次样条生成的曲线更加光滑。在实际建模中，由于我们不知道数据的生成过程，因此这两种插值都可以使用。

说明：

legend(string1,string2,string3, …)

% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。
% ‘Location’用来指定标注显示的位置

figure(1),figure(2)是为了防止多个图像存在时图像被覆盖。

5. n维数据的插值(了解)

p = interpn(x1,x2,...,xn, y, new_x1,newx_2,...,new_xn, method)

x1,x2,...,xn是已知的样本点的横坐标
y是已知的样本点的纵坐标坐标
new_x1,newx_2,...,new_xn是要插入点的横坐标
method是要插值的方法
‘linear’：线性插值（默认算法）；
‘cubic’：三次插值；
‘ spline’ ：三次样条插值法； ( 最为精准 )
‘nearest’：最邻近插值算法。

% n维数据的插值
x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')

四、插值算法用于短期预测

根据过去10年的中国人口数据，预测接下来三年的人口数据。过去10年的数据：

年份	人口(万）
2009	133126
2010	133770
2011	134413
2012	135069
2013	135738
2014	136427
2015	137122
2016	137866
2017	138639
2018	139538

% 人口预测（注意：一般我们很少使用插值算法来预测数据，随着课程的深入，后面的章节会有更适合预测的算法供大家选择，例如灰色预测、拟合预测等）
population=[133126,133770,134413,135069,135738,136427,137122,137866,138639, 139538];
year = 2009:2018;
p1 = pchip(year, population, 2019:2021)  %分段三次埃尔米特插值预测
p2 = spline(year, population, 2019:2021) %三次样条插值预测
figure(4);
plot(year, population,'o',2019:2021,p1,'r*-',2019:2021,p2,'bx-')
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','Location','SouthEast')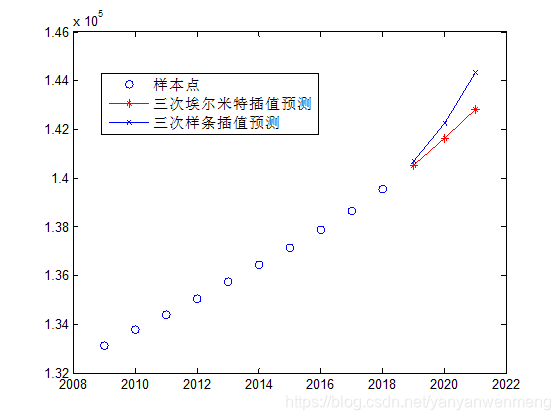

五、实例——数据预处理（补全数据）

原始数据：需要插值得到偶数周轮虫、溶氧等的值。

'周数'	1	3	5	7	9	11	13	15
'轮虫'	1913	1945	1920	2205	2260	2302	2385	2420
'溶氧'	5.12	3.2	6.72	3.36	2.4	4.14	6.43	4.6
'COD'	21.9	20	26.8	27.73	23.4	22.75	25.36	26.03
'水温'	24.8	25.7	26.8	28	30.4	30	27.6	30.8
'PH值'	9.31	9.14	9.14	9.29	9.22	9.33	9.16	9.26
'盐度'	1.8	2.3	1.9	2.1	2.1	1.1	1.5	1.5
'透明度'	28	24	26	22	22	20	19	23
'总碱度'	425.11	457.99	492.48	492.08	501.93	598.48	604.44	623.89
'氯离子'	628.1	639.2	648.87	640.33	616.43	614.72	507.14	580
'透明度'	28	24	26	22	22	20	19	23
'生物量'	30.58	36.19	49.75	60.58	56.58	60.06	67.99	67.74

Z.mat的数据

1	3	5	7	9	11	13	15
1913	1945	1920	2205	2260	2302	2385	2420
5.12	3.2	6.72	3.36	2.4	4.14	6.43	4.6
21.9	20	26.8	27.73	23.4	22.75	25.36	26.03
24.8	25.7	26.8	28	30.4	30	27.6	30.8
9.31	9.14	9.14	9.29	9.22	9.33	9.16	9.26
1.8	2.3	1.9	2.1	2.1	1.1	1.5	1.5
28	24	26	22	22	20	19	23
425.11	457.99	492.48	492.08	501.93	598.48	604.44	623.89
628.1	639.2	648.87	640.33	616.43	614.72	507.14	580
28	24	26	22	22	20	19	23
30.58	36.19	49.75	60.58	56.58	60.06	67.99	67.74

【分析】在进行插值时，以周数为自变量，轮虫量、溶氧量等分别为因变量y1,y2……，使用循环进行插值。

比如原始的自变量：x:1 3 5 7 9 11 13 15

轮虫量y1：1913 1945 1920 2205 2260 2302 2385 2420

需要插值的自变量：new_x,为偶数周，或者为了代码编写方便，可以写成1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

插值后的轮虫量p1=spline(x,y,new_x)

使用方法：subplot（m,n,p）或者subplot（m n p）。

subplot是将多个图画到一个平面上的工具。其中，m表示是图排成m行，n表示图排成n列，也就是整个figure中有n个图是排成一行的，一共m行，如果m=2就是表示2行图。p表示图所在的位置，p=1表示从左到右从上到下的第一个位置。在第p块创建坐标系，并返回它的句柄。

1. 三次埃米尔特插值

%插值预测中间周的水体评价指标
load Z.mat
x=Z(1,:); %Z的第一行是星期Z: 1     3     5     7     9    11    13    15
[n,m]=size(Z);%n为Z的行数，m为Z的列数
% 注意Matlab的数组中不能保存字符串，如果要生成字符串数组，就需要使用元胞数组，其用大括号{}定义和引用
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};  % 等会要画的图形的标签
disp(['共有' num2str(n-1) '个指标要进行插值。'])
disp('正在对一号池三次埃尔米特插值，请等待')%一号池共有十一组要插值的数据，算上星期所在的第一行，共十二行
P=zeros(11,15);%对要储存数据的矩阵P赋予初值
for i=2:n%从第二行开始都是要进行插值的指标
    y=Z(i,:);%将每一行依次赋值给y
    new_x=1:15;%要进行插值的x
    p1=pchip(x,y,new_x);%调用三次埃尔米特插值函数
    subplot(4,3,i-1);%将所有图依次变现在4*3的一幅大图上
    plot(x,y,'ro',new_x,p1,'g-');%画出每次循环处理后的图像
    axis([0 15,-inf,inf])  %设置坐标轴的范围，这里设置横坐标轴0-15，纵坐标不变化
    %  xlabel('星期')%x轴标题
    ylabel(ylab{i})%y轴标题  这里是直接引用元胞数组中的字符串哦
    P(i-1,:)=p1;%将每次插值之后的结果保存在P矩阵中       
end
legend('原始数据','三次埃尔米特插值数据','Location','SouthEast')%加上标注，注意要手动在图中拖动标注到图片右下角哦
P = [1:15; P]  %把P的第一行加上周数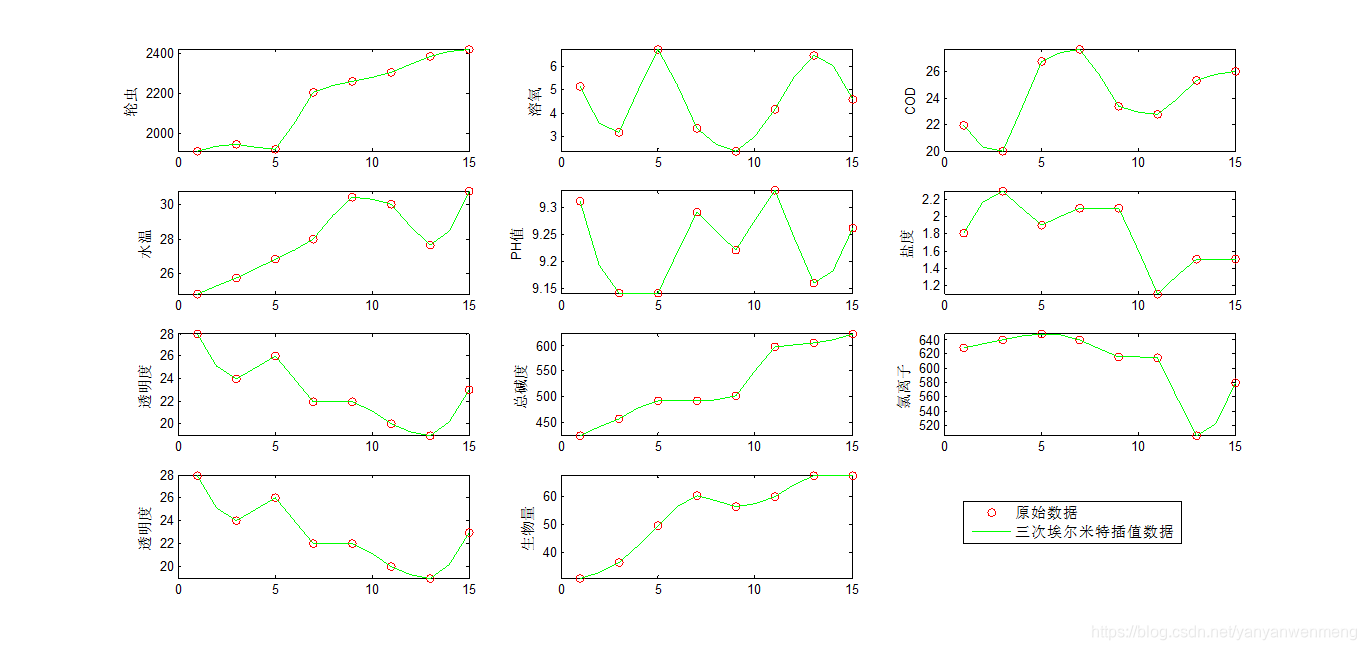

插值后的结果放在p矩阵中，记得保留2位小数就可以了。

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1913.00	1936.56	1945.00	1932.50	1920.00	2050.97	2205.00	2238.07	2260.00	2279.98	2302.00	2344.32	2385.00	2407.28	2420.00
5.12	3.58	3.20	4.96	6.72	5.23	3.36	2.69	2.40	3.02	4.14	5.53	6.43	6.00	4.60
21.90	20.24	20.00	23.20	26.80	27.47	27.73	25.71	23.40	22.93	22.75	23.92	25.36	25.83	26.03
24.80	25.23	25.70	26.23	26.80	27.34	28.00	29.40	30.40	30.29	30.00	28.71	27.60	28.45	30.80
9.31	9.19	9.14	9.14	9.14	9.22	9.29	9.26	9.22	9.28	9.33	9.25	9.16	9.18	9.26
1.80	2.17	2.30	2.10	1.90	2.00	2.10	2.10	2.10	1.60	1.10	1.30	1.50	1.50	1.50
28.00	25.13	24.00	25.00	26.00	24.00	22.00	22.00	22.00	21.17	20.00	19.33	19.00	20.19	23.00
425.11	441.35	457.99	479.44	492.48	492.28	492.08	494.77	501.93	551.04	598.48	601.72	604.44	612.03	623.89
628.10	633.83	639.20	645.33	648.87	646.17	640.33	627.21	616.43	615.60	614.72	560.51	507.14	523.19	580.00
28.00	25.13	24.00	25.00	26.00	24.00	22.00	22.00	22.00	21.17	20.00	19.33	19.00	20.19	23.00
30.58	32.60	36.19	42.46	49.75	56.67	60.58	58.58	56.58	57.72	60.06	64.63	67.99	67.96	67.74

2. 三次样条插值

%插值预测中间周的水体评价指标
load Z.mat
x=Z(1,:); %Z的第一行是星期Z: 1     3     5     7     9    11    13    15
[n,m]=size(Z);%n为Z的行数，m为Z的列数
% 注意Matlab的数组中不能保存字符串，如果要生成字符串数组，就需要使用元胞数组，其用大括号{}定义和引用
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};  % 等会要画的图形的标签
disp(['共有' num2str(n-1) '个指标要进行插值。'])
disp('正在对一号池三次样条插值，请等待')%一号池共有十一组要插值的数据，算上星期所在的第一行，共十二行
P=zeros(11,15);%对要储存数据的矩阵P赋予初值
for i=2:n%从第二行开始都是要进行插值的指标
    y=Z(i,:);%将每一行依次赋值给y
    new_x=1:15;%要进行插值的x
    p1=spline(x,y,new_x);%调用三次样条插值函数
    subplot(4,3,i-1);%将所有图依次变现在4*3的一幅大图上
    plot(x,y,'ro',new_x,p1,'m-')%画出每次循环处理后的图像
    axis([0 15,-inf,inf])  %设置坐标轴的范围，这里设置横坐标轴0-15，纵坐标不变化
    %  xlabel('星期')%x轴标题
    ylabel(ylab{i})%y轴标题  这里是直接引用元胞数组中的字符串哦
    P(i-1,:)=p1;%将每次插值之后的结果保存在P矩阵中       
end
legend('原始数据','三次样条插值','Location','SouthEast')%加上标注，注意要手动在图中拖动标注到图片右下角哦
P = [1:15; P]  %把P的第一行加上周数

%插值预测中间周的水体评价指标
load Z.mat
x=Z(1,:); %Z的第一行是星期Z: 1     3     5     7     9    11    13    15
[n,m]=size(Z);%n为Z的行数，m为Z的列数
% 注意Matlab的数组中不能保存字符串，如果要生成字符串数组，就需要使用元胞数组，其用大括号{}定义和引用
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};  % 等会要画的图形的标签
disp(['共有' num2str(n-1) '个指标要进行插值。'])
disp('正在对一号池三次样条插值，请等待')%一号池共有十一组要插值的数据，算上星期所在的第一行，共十二行
%P=zeros(11,15);%对要储存数据的矩阵P赋予初值
for i=2:n%从第二行开始都是要进行插值的指标
    y=Z(i,:);%将每一行依次赋值给y
    new_x=2:2:15%要进行插值的x，只插值偶数周
    p1=spline(x,y,new_x);%调用三次样条插值函数
    subplot(3,4,i-1);%将所有图依次变现在3*4的一幅大图上
    plot(x,y,'ro',new_x,p1,'m*')%画出每次循环处理后的图像
    axis([0 15,-inf,inf])  %设置坐标轴的范围，这里设置横坐标轴0-15，纵坐标不变化
    %  xlabel('星期')%x轴标题
    ylabel(ylab{i})%y轴标题  这里是直接引用元胞数组中的字符串哦
    %P(i-1,:)=p1;%将每次插值之后的结果保存在P矩阵中       
end
legend('原始数据','三次样条插值','Location','SouthEast')%加上标注，注意要手动在图中拖动标注到图片右下角哦
%P = [1:15; P]  %把P的第一行加上周数

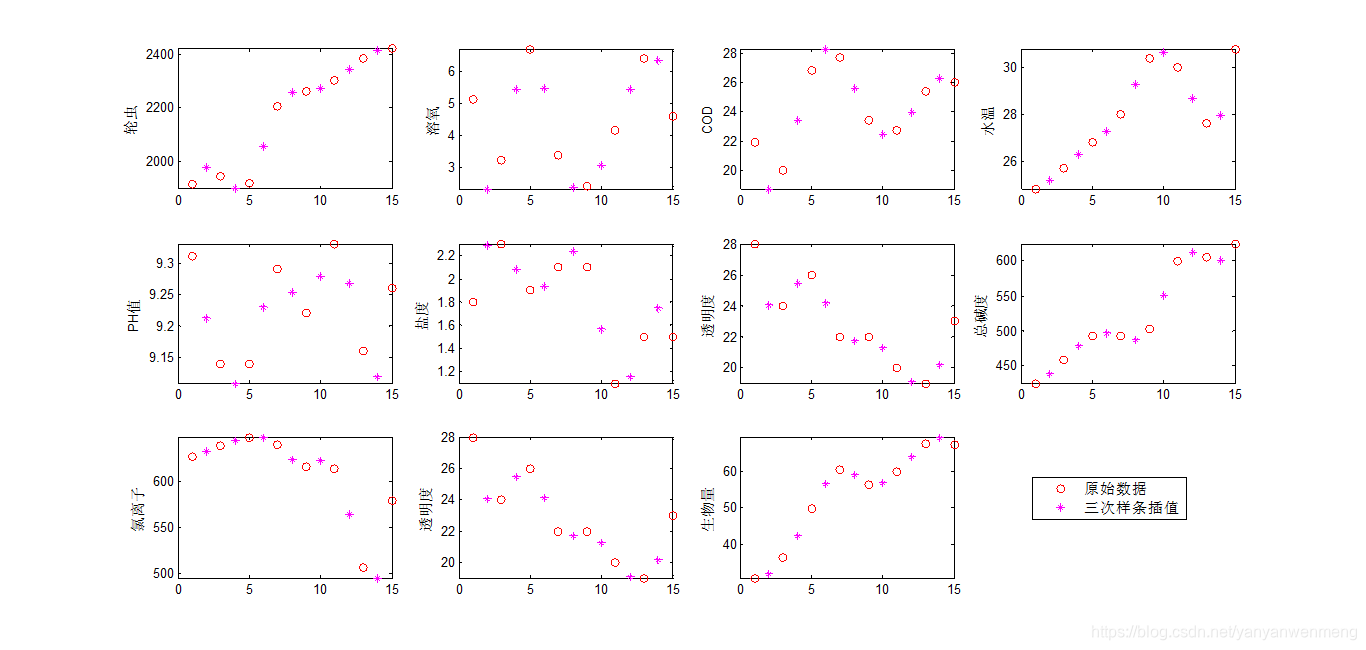
3. 三次样条插值和三次埃尔米特插值的对比

%插值预测中间周的水体评价指标
load Z.mat
x=Z(1,:); %Z的第一行是星期Z: 1     3     5     7     9    11    13    15
[n,m]=size(Z);%n为Z的行数，m为Z的列数
% 注意Matlab的数组中不能保存字符串，如果要生成字符串数组，就需要使用元胞数组，其用大括号{}定义和引用
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};  % 等会要画的图形的标签
disp(['共有' num2str(n-1) '个指标要进行插值。'])
P=zeros(11,15);%对要储存数据的矩阵P赋予初值
for i=2:n%从第二行开始都是要进行插值的指标
    y=Z(i,:);%将每一行依次赋值给y
    new_x=1:15;%要进行插值的x
    p1=pchip(x,y,new_x);%调用三次埃尔米特插值函数
    p2=spline(x,y,new_x);%调用三次样条插值函数
    subplot(4,3,i-1);%将所有图依次变现在4*3的一幅大图上
    plot(x,y,'ro',new_x,p1,'g-',new_x,p2,'m-');%画出每次循环处理后的图像
    axis([0 15,-inf,inf])  %设置坐标轴的范围，这里设置横坐标轴0-15，纵坐标不变化
    %  xlabel('星期')%x轴标题
    ylabel(ylab{i})%y轴标题  这里是直接引用元胞数组中的字符串哦
    %P(i-1,:)=p1;%将每次插值之后的结果保存在P矩阵中       
end
legend('原始数据','三次埃尔米特插值函数','三次样条插值','Location','SouthEast')%加上标注，注意要手动在图中拖动标注到图片右下角哦
%P = [1:15; P]  %把P的第一行加上周数