Perron–Frobenius theorem:
证明方阵,如果其行列的元素为正值,则存在最大的特征值,并且特征向量的每个元素是正的。这个原理应用在统计推断,经济,人口统计学,搜索引擎的基础。
PF原理:说明了最大特征值的作用和实对称矩阵的作用。
如果临界矩阵A是个实对称矩阵,则具有下列性质:
1.There is a positive real number
r, called the
Perron root or the
Perron–Frobenius eigenvalue, such that
r is an eigenvalue of
A and any other eigenvalue
λ (possibly,
complex) is strictly smaller than
r in
absolute value, |
λ| <
r. Thus, the
spectral radius
ρ(
A) is equal to
r.
2.The Perron–Frobenius eigenvalue is simple:
r is a simple root of the
characteristic polynomial of
A. Consequently,
eigenspace associated to
r is one-dimensional. (Same is true for the left eigenspace i.e. eigenspace for
AT.)
3.There exists an eigenvector
v = (
v
1,…,
v
n) of
A with eigenvalue
r such that all components of
v are positive:
A v =
r v,
v
i > 0 for 1 ≤
i ≤
n. (Respectively exists positive left eigenvector
w :
wT A =
r wT,
w
i > 0.)转置就可以了。
4.There are no other positive (moreover non-negative) eigenvectors except
v (respectively the left eigenvectors except
w). I.e. all other eigenvectors must have at least one negative or complex component.
5.
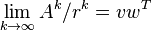 , where the left and right eigenvectors for
A are normalized so that
wTv = 1. Moreover the matrix
v wT is the
spectral projection corresponding to
r, such projection is called the
Perron projection.
, where the left and right eigenvectors for
A are normalized so that
wTv = 1. Moreover the matrix
v wT is the
spectral projection corresponding to
r, such projection is called the
Perron projection.
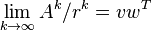 , where the left and right eigenvectors for
A are normalized so that
wTv = 1. Moreover the matrix
v wT is the
spectral projection corresponding to
r, such projection is called the
Perron projection.
, where the left and right eigenvectors for
A are normalized so that
wTv = 1. Moreover the matrix
v wT is the
spectral projection corresponding to
r, such projection is called the
Perron projection.
6.
Collatz–Wielandt formula: for all non-negative non-zero vectors
x let
f(
x) be the minimum value of [
Ax]
i /
x
i taken over all those
i such that
xi ≠ 0. Then
f is a real valued function whose
maximum is the Perron–Frobenius eigenvalue.
7.Min-max Collatz–Wielandt formula is similar to the one above: for all strictly positive vectors
x (pay attention that one above required only non-negativity here) let
g(
x) be the maximum value of [
Ax]
i /
x
i taken over
i. Then
g is a real valued function whose
minimum is the Perron–Frobenius eigenvalue.
8.The Perron–Frobenius eigenvalue satisfies the inequalities:
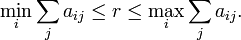
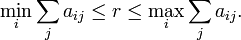
因为在科研中,比如计算pagerank,希望向量的每个值都是正的,在这里我着重介绍定理1,4的证明:
定理四启发式证明:由于不同特征值对应的特征向量是正交的,所以如果有一个特征值对应的特征向量的每个元素大于零,则其余的特征向量的分量要不然是负数要不然就是复数。
数学证明:设
(λ, y)为A的一个特征值和特征向量,(r, x)为A的另一个特征值和特征向量。则r xt y = (xt A) y= xt (A y)=λ xt y。所以r=λ。
定理一证明:矩阵除以矩阵的普半径,最大特征值在半径为1的单位园上。假设有不止一个特征值在这个单位圆上,最后得出矛盾来证明。
























 1224
1224

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








