稀疏attention：Sliding Window Attention高效实现方式

糖葫芦君

已于 2025-03-16 23:25:04 修改

阅读量782

点赞数 30

分类专栏： LLM 文章标签：算法人工智能大模型

于 2025-03-14 18:18:18 首次发布

本文链接：https://blog.csdn.net/yinyu19950811/article/details/146260267

版权

LLM 专栏收录该内容

13 篇文章

订阅专栏

----- 持续更新

SWA （Sliding Window Attention）

改方法来自于mistral-7B论文，该方法假设：生成序列只与前n个路口相关，与前序太远的token无关。处理局部依赖任务（如文本生成）更高效，不适合全局依赖任务（如摘要）。时间复杂度为 $O （ N W ）$

由于我们的场景中序列长度最长不超过300，序列长度比较短，效果基本持平，效率没有提升；可以再尝试将起终点信息的mask去掉。

(1) 注意力范围限制
固定窗口大小：设定一个窗口大小 w，每个 token 仅能关注其前后各 w/2个 token（或仅左侧，取决于任务类型，如自回归生成）。滑动窗口的移动：窗口随 token 位置滑动，但窗口大小固定（如 w=4096）。

(2) 掩码（Mask）设计
通过二进制掩码矩阵强制模型忽略窗口外的 token：

# 示例：生成滑动窗口掩码（PyTorch 伪代码）
seq_len = 8192  # 输入序列长度
window_size = 4096
mask = torch.zeros(seq_len, seq_len)  # 初始化全零掩码

for i in range(seq_len):
    start = max(0, i - window_size // 2)
    end = min(seq_len, i + window_size // 2)
    mask[i, start:end] = 1  # 窗口内设为可见（1）

# 结合因果掩码（自回归生成场景）
causal_mask = torch.triu(torch.ones(seq_len, seq_len), diagonal=1).bool()
final_mask = mask & ~causal_mask  # 窗口内且非未来位置

(3) 分层扩展感受野
多层的窗口叠加：通过堆叠多个注意力层，每个层的窗口覆盖局部区域，高层神经元间接融合更大范围的信息。例如：假设每层窗口大小为 4096，堆叠 4 层后，理论感受野可达 4096x4=16384 token。

（4）高效计算技巧：

块计算（Block Computation）：将长序列切分为多个块，逐块计算注意力，避免一次性处理全序列。
FlashAttention 结合：利用 FlashAttention 的硬件优化加速窗口内注意力计算。

# 示例：使用 FlashAttention 的滑动窗口（伪代码）
from flash_attn import flash_attn_qkvpacked_func

q = ...  # Query 向量
k = ...  # Key 向量
v = ...  # Value 向量
window_mask = ...  # 滑动窗口掩码

# 应用滑动窗口掩码
attn_output = flash_attn_qkvpacked_func(
    q, k, v,
    softmax_scale=1.0,
    causal=True,  # 自回归生成需启用因果掩码
    window_size=window_size  # 直接指定窗口大小
)

问题

这个SWA代码看起来只是额外计算了一个mask矩阵，加入到原矩阵上进行attention计算，计算复杂度并没有改变吧？反而增加了一个构造mask矩阵的时间。有清楚的朋友可以帮忙解答一下吗

问deepseek：
在这里插入图片描述
deepseek说我的猜想是没问题的，

您提出的问题非常关键！您是对的——如果直接在完整的注意力矩阵上应用滑动窗口掩码，计算复杂度仍然是 $O（n^2）$ ，因为即使掩码将窗口外的值设为负无穷，模型仍然需要计算所有位置的注意力分数。这与 Sliding Window Attention（SWA）的理论设计目标复杂度 $O （ n w ）$ 存在矛盾。

实际高效的 SWA 需直接跳过窗口外的计算，仅处理窗口内的 token。以下是两种主流实现方案：

方案 1：分块计算（Block-wise Computation）
将长序列切分为多个块（Block），每个块内独立计算注意力，避免全局矩阵操作。
在这里插入图片描述

import torch
from einops import rearrange

def block_swa(q, k, v, window_size):
    # 输入 q, k, v: [batch, seq_len, heads, dim]
    batch, seq_len, heads, dim = q.shape
    
    # 分块（假设 seq_len 是 window_size 的整数倍）
    q_blocks = rearrange(q, 'b (n w) h d -> b n w h d', w=window_size)
    k_blocks = rearrange(k, 'b (n w) h d -> b n w h d', w=window_size)
    v_blocks = rearrange(v, 'b (n w) h d -> b n w h d', w=window_size)
    
    # 块内注意力计算（复杂度 O(n * w^2)）
    attn = torch.einsum('bnqhd,bnkhd->bnhqk', q_blocks, k_blocks) / (dim ** 0.5)
    attn = torch.softmax(attn, dim=-1)
    out_blocks = torch.einsum('bnhqk,bnkhd->bnqhd', attn, v_blocks)
    
    # 合并块
    out = rearrange(out_blocks, 'b n w h d -> b (n w) h d')
    return out

方案 2：稀疏注意力计算（Sparse Attention）
直接为每个查询（Query）位置仅计算窗口内的键（Key）和值（Value），跳过无关位置。
在这里插入图片描述

def sparse_swa(q, k, v, window_size):
    batch, seq_len, heads, dim = q.shape
    output = torch.zeros_like(q)
    
    for i in range(seq_len):
        # 确定窗口边界
        start = max(0, i - window_size // 2)
        end = min(seq_len, i + window_size // 2)
        
        # 收集窗口内的 k 和 v [batch, heads, window_size, dim]
        k_window = k[:, start:end, :, :]
        v_window = v[:, start:end, :, :]
        
        # 计算当前查询位置的注意力
        q_i = q[:, i, :, :]  # [batch, heads, dim]
        attn_scores = torch.einsum('bhd,bhwd->bhw', q_i, k_window) / (dim ** 0.5)
        attn_weights = torch.softmax(attn_scores, dim=-1)
        
        # 加权求和
        output[:, i, :, :] = torch.einsum('bhw,bhwd->bhd', attn_weights, v_window)
    
    return output

复杂度：O(n×w)（严格符合理论值）。

局限性：循环操作在 GPU 上效率低，需用 CUDA 内核优化。

实际方案：FlashAttention支持直接指定窗口大小，自动跳过窗口外计算，无需显式分块或循环： 若需自行实现 SWA，建议优先使用优化库（如 FlashAttention），避免手动处理复杂的分块和索引逻辑。

# 使用 FlashAttention 的滑动窗口模式
from flash_attn import flash_attn_func

output = flash_attn_func(
    q, k, v,
    causal=True,
    window_size=window_size  # 直接限制窗口大小
)

在这里插入图片描述

Longformer-2020

作者共提出了三种新的attention机制，这三种方法都很好的降低了传统self-attention的复杂度，它们分别是滑窗机制、空洞滑窗机制（扩大单层感受野）、融合全局信息的滑窗机制

Longformer在两个字符级语言建模任务上都取得了SOTA的效果。并且作者用Longformer的attention方法继续预训练RoBERTa，训练得到的语言模型在多个长文档任务上进行fine-tune后，性能全面超越RoBERTa

在这里插入图片描述

讲解很好的博客：
https://blog.csdn.net/qq_37236745/article/details/109675752 其中对空洞滑动机制的效果进行了理论质疑。

实验中提出由底至高层递增窗口大小，可以提升性能；反之则降低
在这里插入图片描述

transformer-XL-2019

由于序列长度过长，所以transformer有时需要分段建模，但是分段建模的缺点：

段与段之间是分离的
推理时每次都要从头构建一次上下文，推理速度慢

在这里插入图片描述
transformer-XL利用循环机制（段与段之间的依赖）

不仅利用前面隐藏层的输出，而且还利用了上一段的输出，建立长期依赖关系
推理时：每次前进一整个段，并利用之前段的数据预测当前段的输出

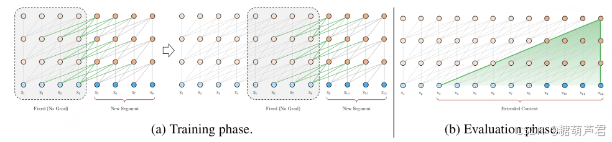
段循环机制（Segment-Level Recurrence）
核心思想：在训练时缓存前一段的隐藏状态，并在处理当前段时复用这些状态，实现跨段上下文传递。

实现步骤：

缓存前段隐藏状态：前一段的隐藏状态
$H_{prev}∈R^{L×d}$ ，L为段长度）被保存。
与当前段拼接：当前段输入 $H_{curr}∈R^{L×d}$ 与 $H_{prev}$ 拼接为 $H_{concat}\in R^{2Ld}$
计算注意力：对拼接后的序列计算自注意力，但仅更新当前段的梯度。
更新缓存：将当前段的隐藏状态加入缓存，供下一段使用。

复杂度仍为 $O(L^2d)$ ，但有效建模长度 $N \times L$ ( $N$ 为段数）。通过段循环机制，实际建模的上下文长度可达数千token。使用xl要建立长序列依赖关系的话，需要把mems每次调用的时候反复传入才可以建立长序列依赖。突破了传统Transformer的单段长度限制。其设计平衡了效率与性能，成为长序列任务（如语言建模、文本生成）的重要基础架构。后续模型如XLNet、Compressive Transformer均基于此思想进一步优化。

相对位置编码（Relative Positional Encoding）
传统Transformer的绝对位置编码无法适应不同段的位置关系。Transformer-XL引入相对位置编码：

绝对位置编码的问题：
当序列跨越多个段时，相同位置在不同段的绝对位置不同，导致位置编码冲突。

相对位置编码的优势：
编码位置差异（相对距离）而非绝对位置，解决跨段位置一致性问题。

参考：

Longformer：https://arxiv.org/abs/2004.05150arxiv.org
https://blog.csdn.net/m0_72947390/article/details/134949443
Longformer实现：
https://github.com/huggingface/transformers/issues/16610
https://zhuanlan.zhihu.com/p/473076723
SWA： https://blog.csdn.net/m0_62053105/article/details/140154494
transformer-XL：https://blog.csdn.net/Magical_Bubble/article/details/89060213?spm=1001.2101.3001.6650.3&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-3-89060213-blog-121243192.235%5Ev43%5Epc_blog_bottom_relevance_base9&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-3-89060213-blog-121243192.235%5Ev43%5Epc_blog_bottom_relevance_base9&utm_relevant_index=6