蒙特卡洛模拟及应用

最新推荐文章于 2025-04-10 17:55:27 发布

Daytoy Studio

最新推荐文章于 2025-04-10 17:55:27 发布

阅读量5.6k

点赞数 5

分类专栏： MATLAB学习笔记文章标签： matlab 算法

本文链接：https://blog.csdn.net/yixon_oss/article/details/130795163

版权

MATLAB学习笔记专栏收录该内容

1 篇文章

订阅专栏

概述

蒙特卡洛模拟也称蒙特卡洛方法、统计模拟方法、随机模拟方法，是一种基于概率统计原理解决问题的方法, 由著名的数学家和计算机科学家冯·诺依曼提出.

原理与步骤

问题分析，建立概率统计模型，问题解与模型某个变量或参数对应.
模拟仿真试验，根据模型生成一定数量的变量的随机数.
试验结果统计与分析，求出问题最终解.

特点

针对复杂程度高，难以建立准确模型的问题，或模型复杂不易求解的问题.

问题的解能与某个事件的概率或与概率相关的变量相关联.

预备知识：随机数

（1）rand指令：生成(0,1)之间均匀分布随机数.

rand(n) n*n随机数矩阵.

rand(m,n) m*n随机数矩阵.

rand(m,n,‘p’) 指定精度随机数矩阵，p可选double或single.

rand(size(A)) 与A规模相同随机数矩阵.

hist(y) 绘制频数分布直方图

（2）randn指令：生成标准正态分布随机数，均值0，标准差1.

（3）randi指令：生成均匀分布的整随机数.

randi(imax,n) 生成在[1:imax]之间均匀分布的n*n整数随机数矩阵.

randi([imin,imax],m,n) 生成[imin,imax]间m*n矩阵.

（4）mnrnd：生成多元分布随机数.

r=mnrnd(n,p) 生成随机向量r. n表示向量中元素之和，p是1*K向量，将所有元素划分为K组，p中的元素表示每组的比例，p的元素之和必须等于1. r是一个1&k的向量，给出每组中元素的个数.

r=mnrnd(n,p,m) 生成m个随机向量，r是m*K矩阵，每行对应一个多元分布随机数向量.

>>n=10;
>> p=[0.4 0.2 0.4];
>> r1=mnrnd(n,p)

r1 =

     3     1     6

>> r1=mnrnd(n,p,6)

r1 =

     6     3     1
     5     2     3
     6     3     1
     4     0     6
     6     1     3
     2     3     5

>> hist3(r1(:,1:2),[10,10])

hist

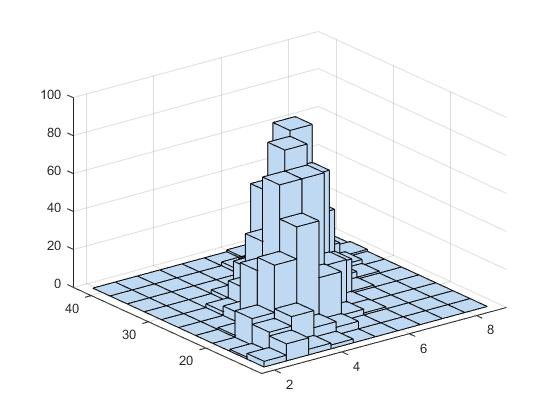
（5）mvnrnd：多元正态分布随机数

r=mvnrnd(mu,sigma) 返回向量r，mu是d维均值向量，sigma是协方差矩阵.

r=mvnrnd(mu,sigma,n) 返回n*d矩阵r.

>> mu=[5 25];
>> sigma=[1 4;4 25];
>> a0=mvnrnd(mu,sigma)

a0 =

    4.4804   22.0201

>>a=mvnrnd(mu,sigma,1000);
>> hist3(a,[10,10])

mvnrndhist

（6）随机数的操作

改变随机数的范围：产生[a,b]间随机数

*r=a+(b-a).rand(1,n)

改变正态分布随机数的均值和标准差

*r=m+s.randn(1,n) 均值改为m，标准差n

重置随机数发生器产生相同随机数 :人为控制产生的随机数

rng(‘default’)

>>  rng('default')
rand(1,8)%两条一起运行三次

ans =

    0.8147    0.9058    0.1270    0.9134    0.6324    0.0975    0.2785    0.5469
ans =

    0.8147    0.9058    0.1270    0.9134    0.6324    0.0975    0.2785    0.5469
ans =

    0.8147    0.9058    0.1270    0.9134    0.6324    0.0975    0.2785    0.5469

保存随机数发生器的设置重复产生相同的随机数

s=rng;
u1=rand(1,6)
rng(s);
u2=rand(1,6)
rng(s);
u3=rand(1,6)

u1 =

    0.9575    0.9649    0.1576    0.9706    0.9572    0.4854

u2 =

    0.9575    0.9649    0.1576    0.9706    0.9572    0.4854

u3 =

    0.9575    0.9649    0.1576    0.9706    0.9572    0.4854

%第二次
u1 =

    0.8003    0.1419    0.4218    0.9157    0.7922    0.9595

u2 =

    0.8003    0.1419    0.4218    0.9157    0.7922    0.9595

u3 =

    0.8003    0.1419    0.4218    0.9157    0.7922    0.9595

应用实例——模拟投掷硬币

tabulate(X) 输出列表形式，统计向量X中各元素出现频数及概率

投掷硬币：正面1，反面0，每次投掷结果就是随机产生0或1.

r=randi(2,1,1);%产生随机数1或2
r1=r-1;%产生随机数0或1

投掷硬币次数越多，出现正反面的概率越趋于各占1/2.

r10=randi(2,1,10)-1;
r50=randi(2,1,50)-1;
r100=randi(2,1,100)-1;
r1000=randi(2,1,1000)-1;
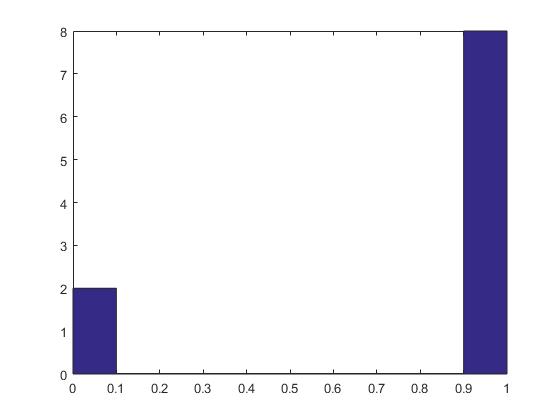
hist(r10)
figure(2)
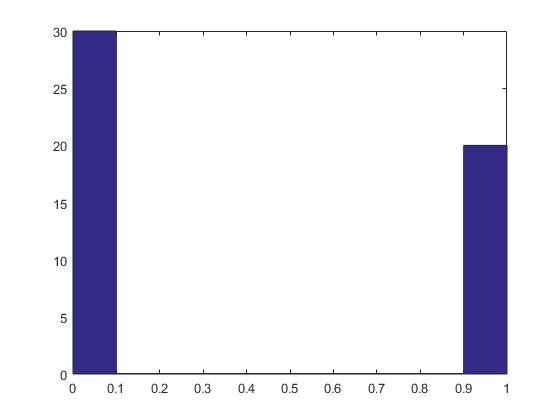
hist(r50)
figure(3)
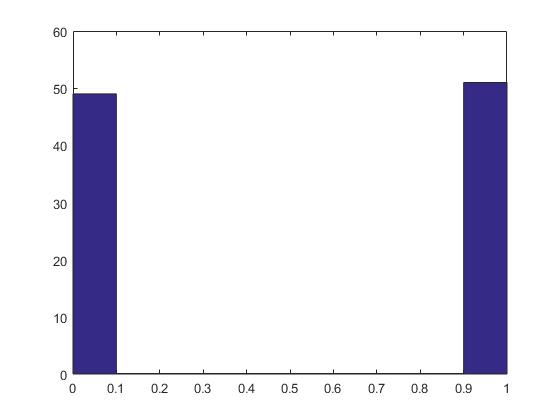
hist(r100)
figure(4)
hist(r1000)
p10=tabulate(r10)%投掷10次时，0和1各自出现的次数及概率
p50=tabulate(r50)
p100=tabulate(r100)
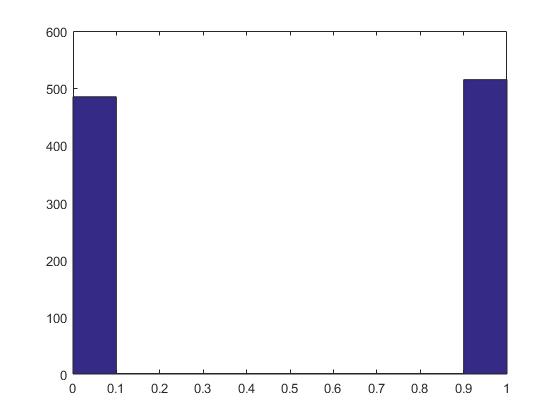
p1000=tabulate(r1000)%投掷1000次时，0和1各自出现的次数及概率

p10 =

     0     2    20
     1     8    80

p50 =

     0    30    60
     1    20    40

p100 =

     0    49    49
     1    51    51

p1000 =

         0  485.0000   48.5000
    1.0000  515.0000   51.5000

randi10

randi50

randi100

randi1000

模拟投骰子

X=randi(6,1,10000000);
tabulate(X)
hist(X)

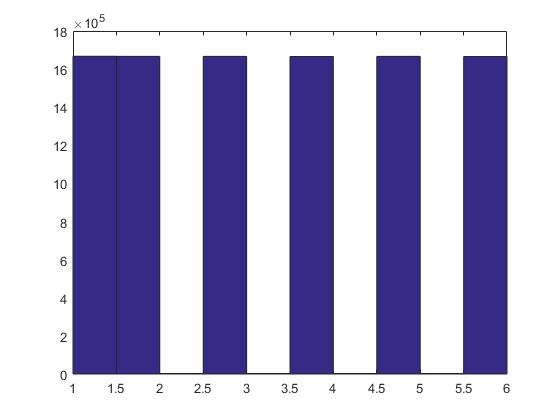
Value    Count   Percent
      1    1667302     16.67%
      2    1666712     16.67%
      3    1666808     16.67%
      4    1666082     16.66%
      5    1667152     16.67%
      6    1665944     16.66%

randi6

蒙特卡洛应用实例

1.计算圆周率π值

总体思想：投点计算.

往边长为1的正方形中随机投点，点落在弧线内部中的概率p是弧线包围的面积与正方形面积之比.

弧线包围面积 $=\frac{πa^2}{4}=\frac{\pi}{4}$

概率 $p=\frac{\pi}{4}$

$π = 4 p .$

用蒙特卡洛模拟统计出p值，就可以计算π.

function [pi]=MCpi(n)
x=rand(n,1);
y=rand(n,1);
count=0;
for i=1:n
if (x(i)^2+y(i)^2<=1)
count=count+1;
end
end
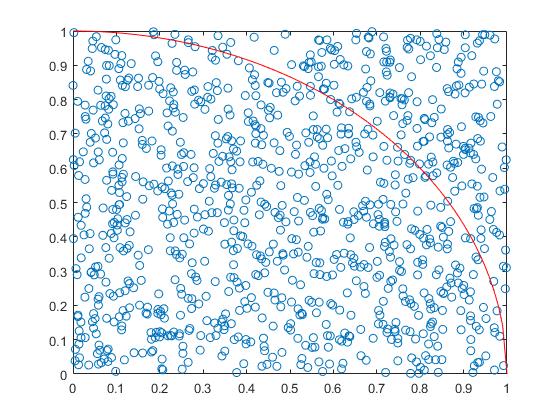
plot(x,y,'o')
hold on
x0=0:0.01:1;
y0=sqrt(1-x0.^2);
plot(x0,y0,'r-');
pi=4*count/n %计算pi值
end

[pi]=MCpi(1000) %1000个随机点做模拟
pi =

    3.1880

function [pi]=MC1pi(n)
%另一个程序，感觉慢
m=0;
for i=1:n
x=rand;
y=rand;
plot(x,y,'o')
hold on
x0=0:0.01:1;
y0=sqrt(1-x0.^2);
plot(x0,y0,'r-');
if (x^2+y^2<=1)
m=m+1;
end
end


pi=4*m/n %计算pi值
end

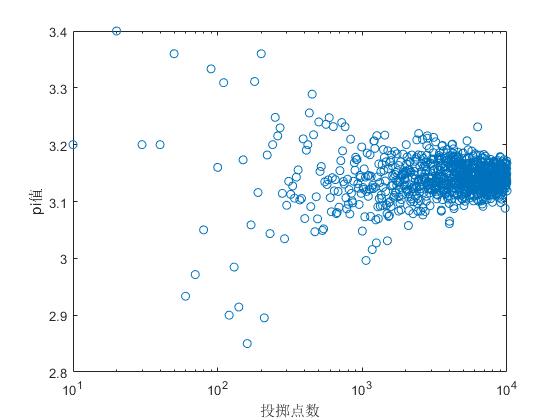
为了解投点次数对pi计算值的影响，绘制pi计算值随投点次数变化趋势图.

n=[10:10:1000];
t=length(n);
pi=zeros(1,t);
for i=1:t
x=rand(n(i),1);
y=rand(n(i),1);
m=sum( x.^2+y.^2<=1); %落在圆内的点数
pi(i)=4*m/n(i);
end
semilogx(n,pi,'o')
xlabel('投掷点数')
ylabel('pi值')

pitrend

2.计算定积分：投点法

例：计算函数
$y=x^{\frac{1}{2}}-x^2$
在[0,1]间的定积分.

int.

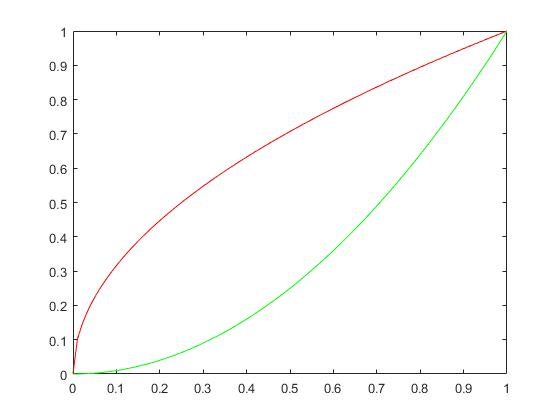
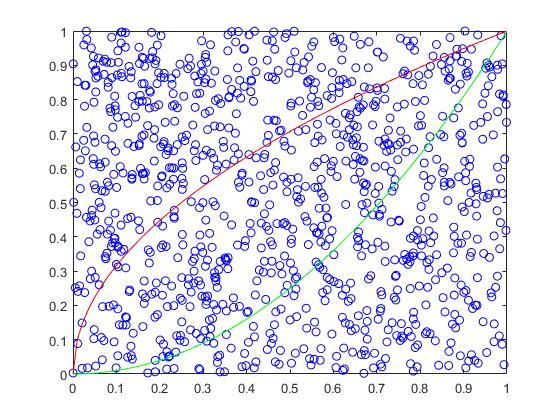
在 $[0, 1]$ 定积分实质是两个函数围成的面积.

function [s] = MCint(n)
%利用蒙特卡洛计算定积分
m=0;
for i=1:n
    x=rand;
    y=rand;
    plot(x,y,'bo')
    hold on
    x0=0:0.01:1;
    y0=sqrt(x0);
    y1=x0.^2;
    plot(x0,y0,'r-',x0,y1,'g-');
    if (sqrt(x)>y && y>x^2)
        m=m+1;
    end
end
s=m/n;
end

[s] = MCint(1000)

s =

    0.3400

MCint

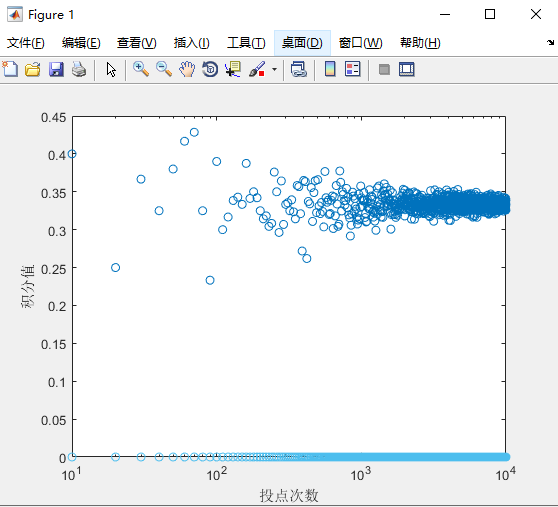
绘制积分值随投点次数的变化趋势图.

n=10:10:10000;
t=length(n);
s=zeros(t);
for i=1:length(n)
x=rand(n(i),1);
y=rand(n(i),1);
m=sum( sqrt(x)>=y & y>x.^2);
s(i)=m/n(i);
end
semilogx(n,s,'o');
xlabel('投点次数');
ylabel('积分值');

MCinttrend

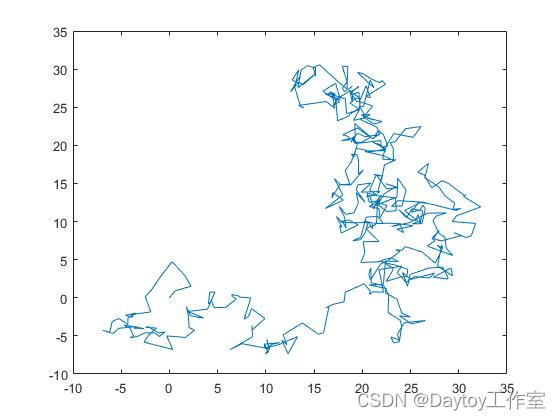
3.模拟布朗运动

模拟微粒的布朗运动.

(1) 模拟二维布朗运动

n=500;
a=randn(1,n);
b=randn(1,n);
x(1)=0;
y(1)=0;
for k=1:n
x(k+1)=x(k)+a(k);
y(k+1)=y(k)+b(k);
end
plot(x,y)

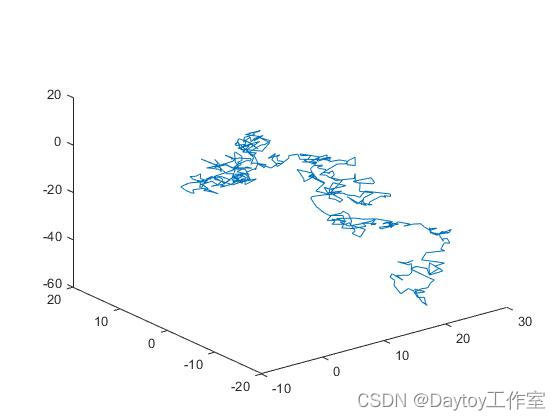
请添加图片描述

(2) 三维布朗运动

n=500;
a=randn(1,n);
b=randn(1,n);
c=randn(1,n);
x(1)=0;
y(1)=0;
z(1)=0;
for k=1:n
x(k+1)=x(k)+a(k);
y(k+1)=y(k)+b(k);
z(k+1)=z(k)+c(k);
end
plot(x,y,z)

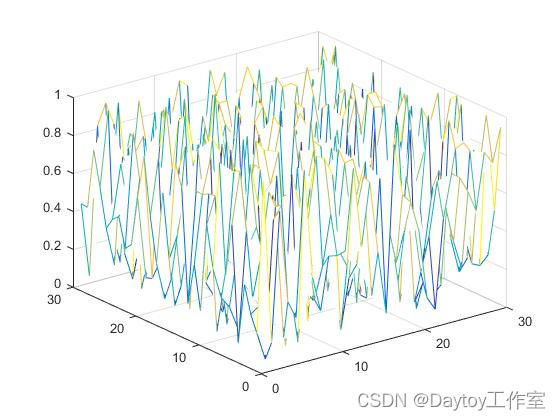
请添加图片描述

4.物体表面形貌近似

可以利用蒙特卡洛模拟表面的微观形貌，基本思路是随机投点，统计各位置落下点的数量，数量与直径或厚度之积就是各位置高度.

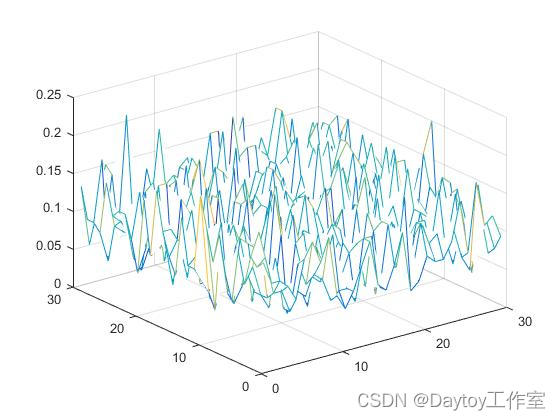
x=1:30; %横坐标范围
y=1:30; %纵坐标范围
z=rand(30); %不同位置厚度
mesh(x,y,z)  %表面网线图
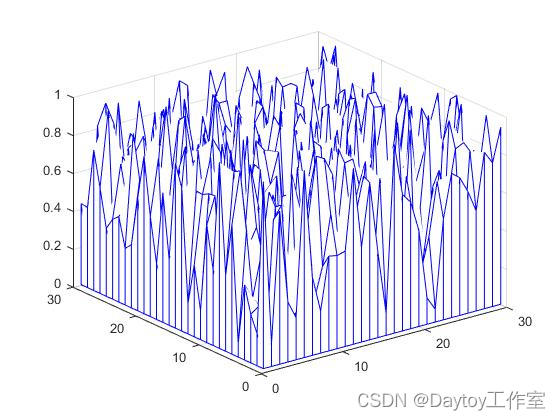
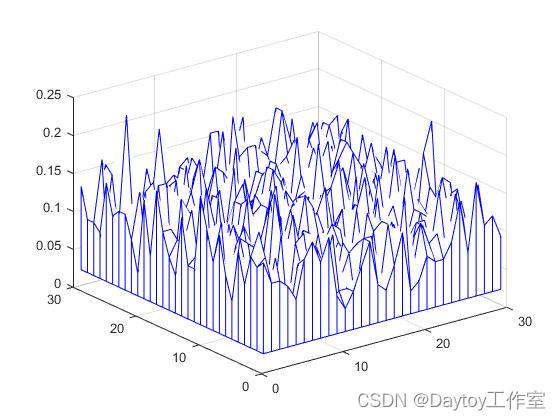
figure(2)
meshz(x,y,z)  %幕帘网线图
colormap([0 0 1])
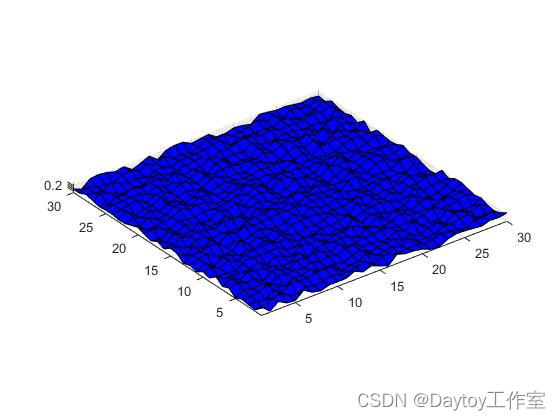
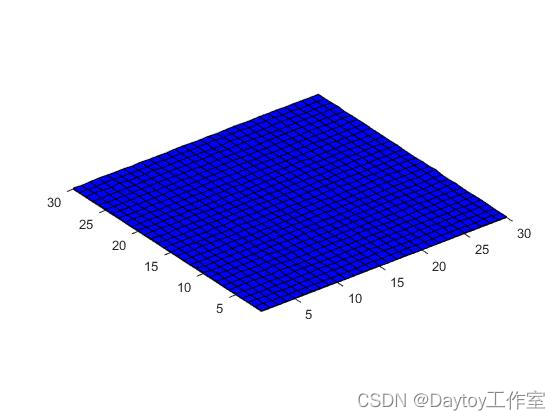
figure(3)
surf(x,y,z)  %曲面图
colormap([0 0 1])
axis('equal')

请添加图片描述

编写其他程序实现

%产生1~900共900个随机数；900表示位置，30*30；产生10次，代表喷涂了10层颗粒
a=randi(900,1,900*10);
n=tabulate(a);
n1=n(:,2)*0.01; %表示各位置厚度
x=1:30;
y=1:30;
z=zeros(30,30);
for i=1:30
z(i,:)=n1((i*30-29):i*30,1)';
end
mesh(x,y,z)
figure(2)
meshz(x,y,z)
colormap([0 0 1])
figure(3)
surf(x,y,z)
colormap([0 0 1])
axis('equal')

请添加图片描述

5.材料成分设计与质量控制

制备新材料时，材料的每种成分的实际含量会与目标含量产生一定的误差，对材料性能会产生影响. 利用蒙特卡洛对材料制备进行模拟，预测最终性能；反过来通过成分设计对质量进行控制.

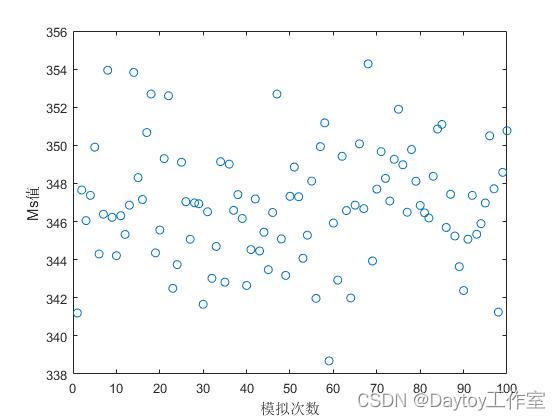
例：Ms是材料的一个性能指标，与材料化学成分有关. 用蒙特卡洛方法对材料的成分设计进行模拟，预测Ms点.

sigma=0.01; %成分的误差
n=100; %模拟次数
C=normrnd(0.3,sigma,1,n);
Mn=normrnd(1.2,sigma,1,n);
Cr=normrnd(0.3,sigma,1,n);
Ni=normrnd(0.2,sigma,1,n);
Mo=normrnd(0.1,sigma,1,n);
Si=normrnd(0.4,sigma,1,n);
Ms=520-321*C-50*Mn-30*Cr-20*Ni-20*Mo-5*Si; %根据元素含量计算Ms点
plot(Ms,'o')
xlabel('模拟次数')
ylabel('Ms值')
figure(2)
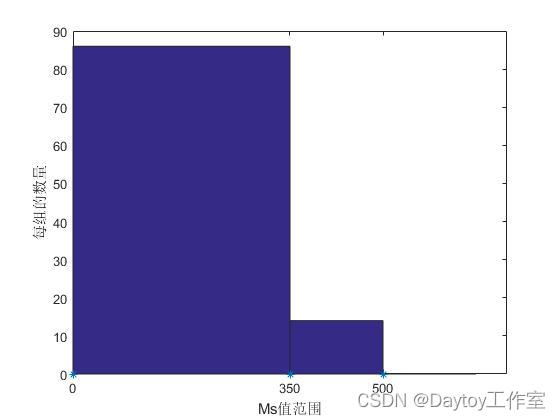
edgs=[0 350 500] %按Ms的值对制备材料进行分组
[n bin]=histc(Ms,edgs); %统计每组的数量 bin是第几组
bar(edgs,n,'histc')  %绘制条形图
xlabel('Ms值范围')
ylabel('每组的数量')

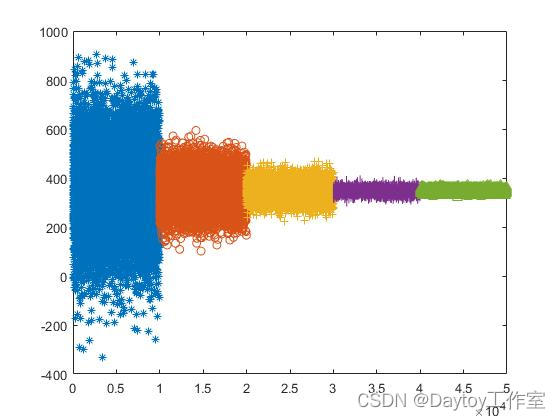
请添加图片描述

为了了解误差对性能稳定性的影响，绘制性能随误差控制值的变化趋势图.

Sigma=[0.5 0.2 0.1 0.05 0.02];
n=10000;
Ms=zeros(5,n);
for i=1:5
sigma=Sigma(i);
C=normrnd(0.3,sigma,1,n);
Mn=normrnd(1.2,sigma,1,n);
Cr=normrnd(0.3,sigma,1,n);
Ni=normrnd(0.2,sigma,1,n);
Mo=normrnd(0.1,sigma,1,n);
Si=normrnd(0.4,sigma,1,n);
Ms(i,:)=520-321*C-50*Mn-30*Cr-20*Ni-20*Mo-5*Si; %根据元素含量计算Ms点
end
x1=1:10000;
plot(x1,Ms(1,:),'*')
hold on
x2=10001:20000;
plot(x2,Ms(2,:),'o')
hold on
x3=20001:30000;
plot(x3,Ms(3,:),'+')
hold on
x4=30001:40000;
plot(x4,Ms(4,:),'-')
hold on
x5=40001:50000;
plot(x5,Ms(5,:),'^')

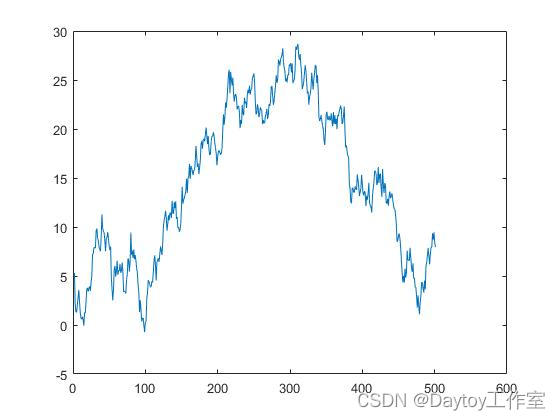
请添加图片描述

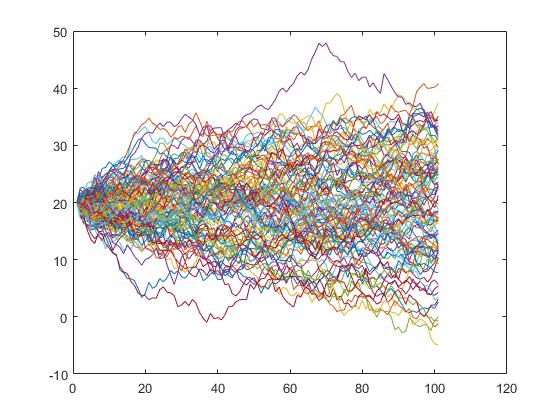
6.模拟股票价格

用蒙特卡洛模拟股票价格变化情况.

p(1)=5; %原始股价
s=500; %模拟天数
a=randn(1,s); %股票变化
for k=1:s
p(k+1)=p(k)+a(k); %每天的股价
end
plot(p)

请添加图片描述

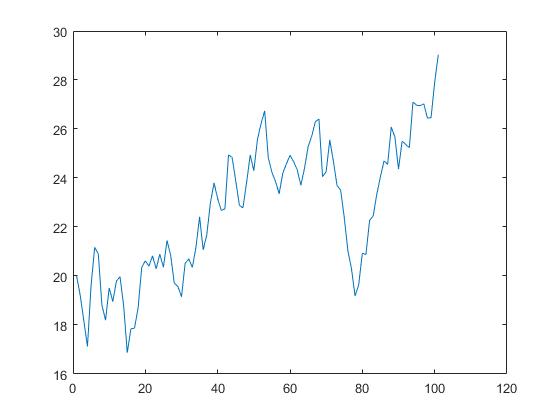
另一个程序

p0=20; %原始股价
s=100; %模拟天数
t=1;  %模拟次数，股票变化可能性
a=randn(s,t);
tend=cumsum([p0*ones(1,t) a]); %最新股价
plot(tend)

p0=20; %原始股价
s=100; %模拟天数
t=100;  %模拟次数，股票变化可能性
a=randn(s,t);
tend=cumsum([p0*ones(1,t) a]); %最新股价
plot(tend)
%100种可能性