排序-选取

1.快速排序（quick sort）

与mergesort都属于分而治之，区别在于mergesort易分，主要精力在合；quicksort易合，主要精力在分，找到轴点，即partition( Rank lo, Rank hi )函数。

 partition( Rank lo, Rank hi )实现：

看似_elem【0】被替代了，其实记录下的pivot值在就是elem【0】，在最后找到了适合它的位置，需要O（n）时间。稳定性一方面等于pivot的值如果很多个，那么以前在第一个的pivot次序改变，而且左侧的相同大元素的位置也发生了前后颠倒。

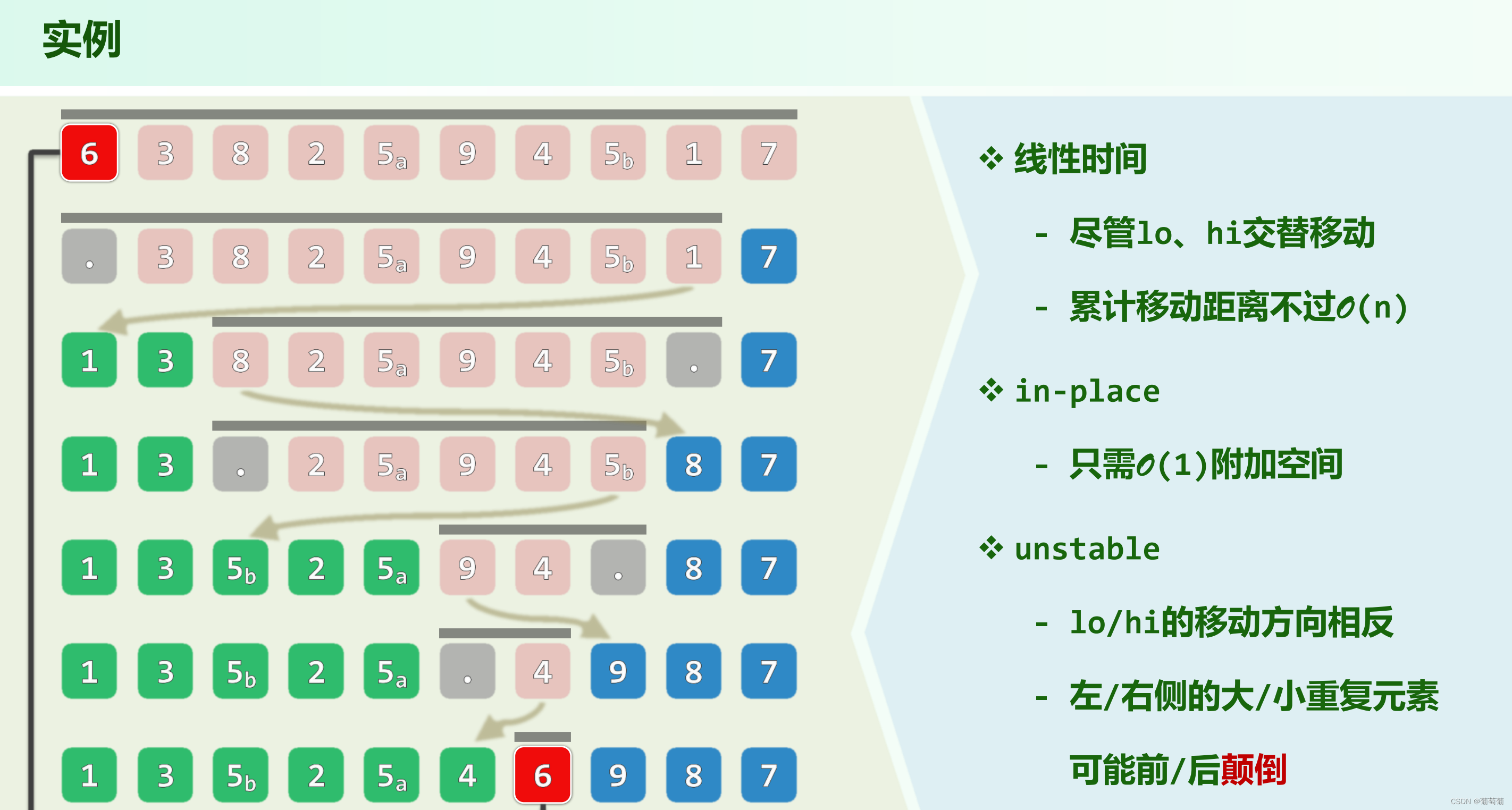
注意递归深度与递归实例总数是不一样的，前者是最多同时有几个函数，后者是累计有多少递归实例，前者是空间复杂度的主要影响因素，后者是时间复杂度的主要影响因素。

最差结果：空间复杂度O（n），时间复杂度O（n^2）

最好结果：空间复杂度O（logn），时间复杂度O（nlogn）（可以看到其实是因为每一层的递归实例加起来的时间都是n）

，

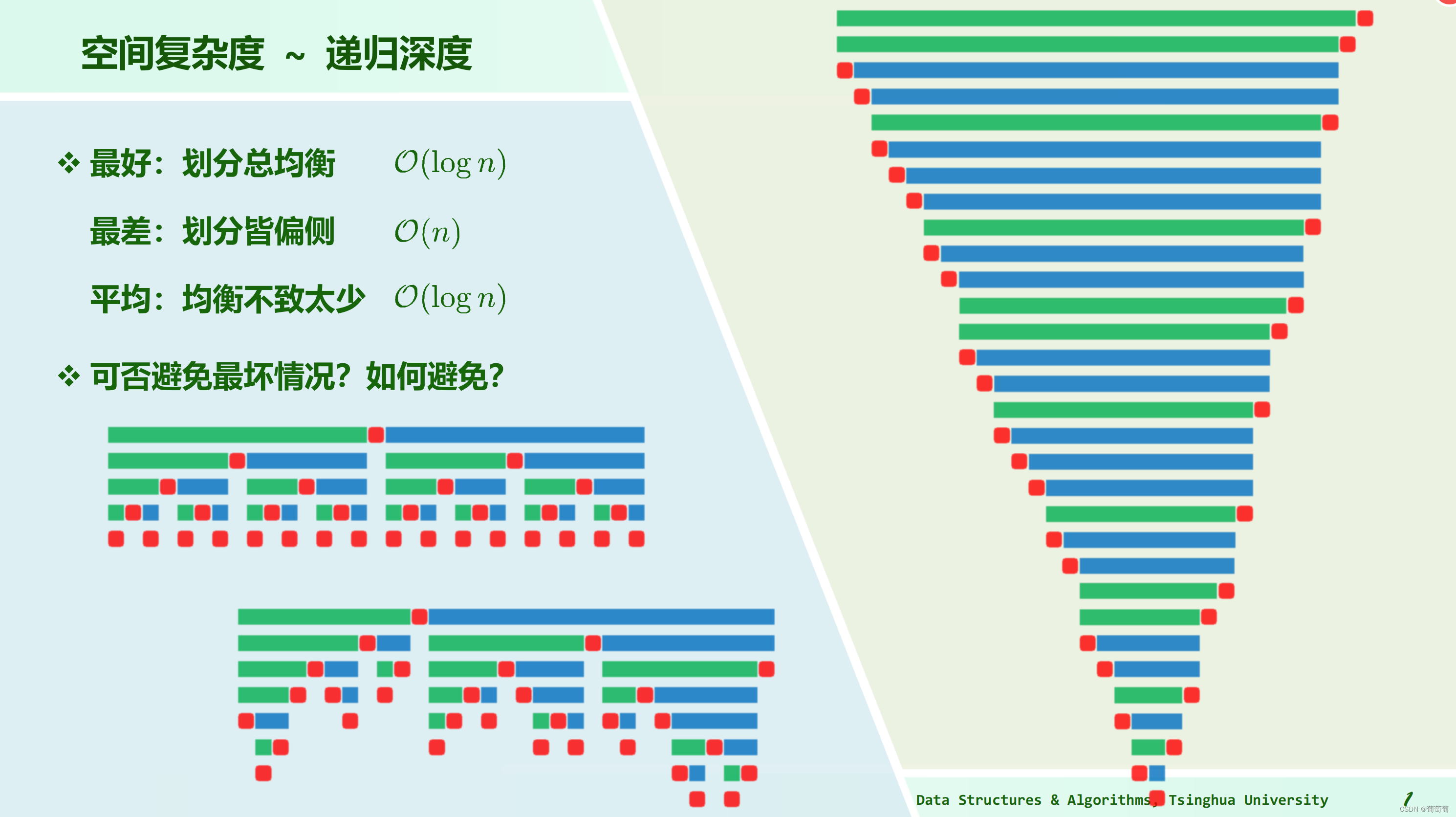
 改为迭代版之后，时间复杂度最坏也还是O（n^2），但是引入的栈空间不过O（logn）。

 虽然直觉上来讲，在期望上递归深度是O（logn），但是下面的证明相反情况概率那里应该是大于号吧。可以这么理解，一个人有k滴血，有m的概率递归一层掉一滴，那么在km次是就很大概率已经g了，如果没g再给个常数乘积上去，g掉的概率很大。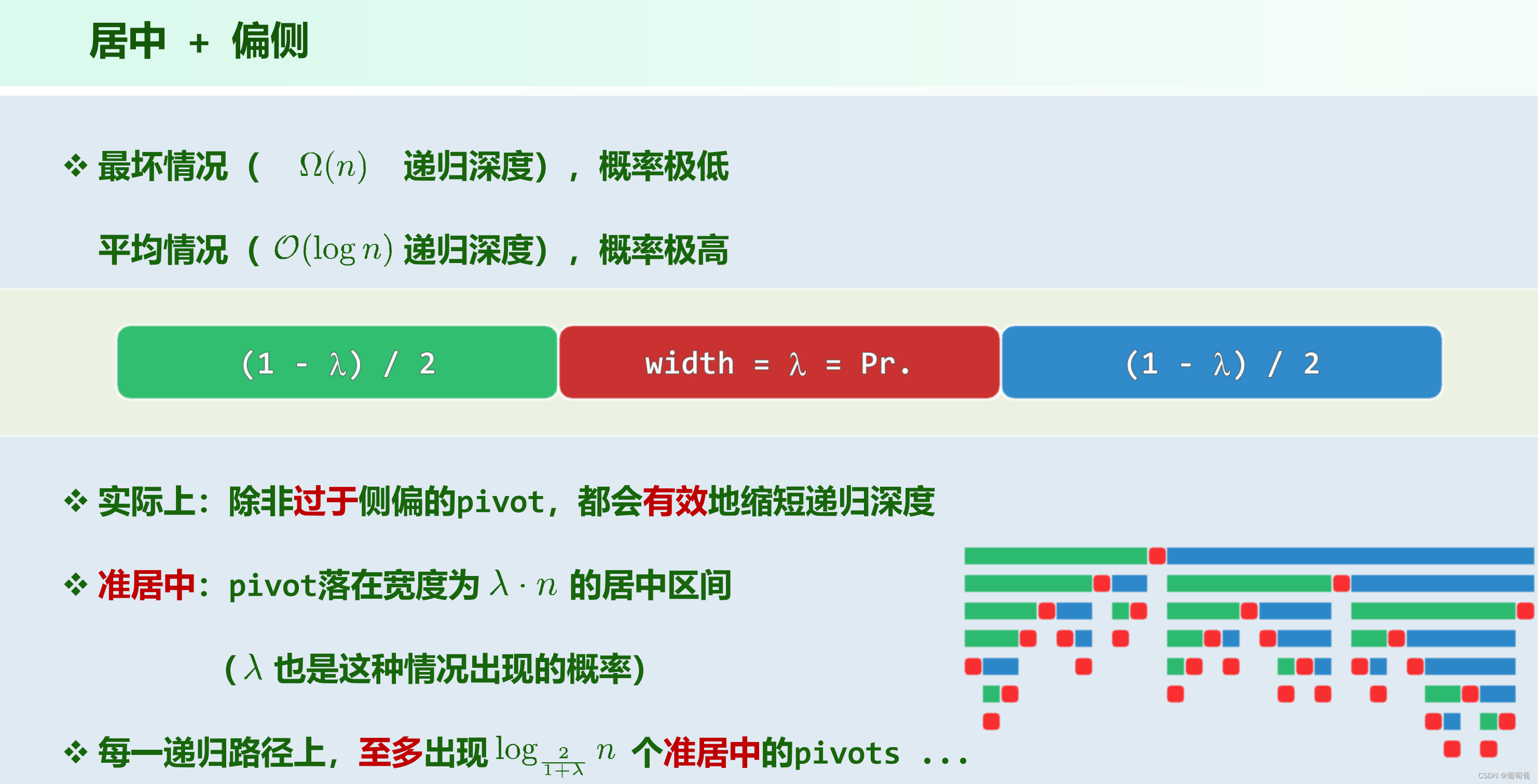

期望的时间复杂度方面（下面的logn是以2为底的）

这里的意思是， Pr（i，j）等于2/j-i+1,即大概等于2 除以两者距离，因为要两端先于中间被确定，如果是两个相邻的i ， j ，概率是 1 。

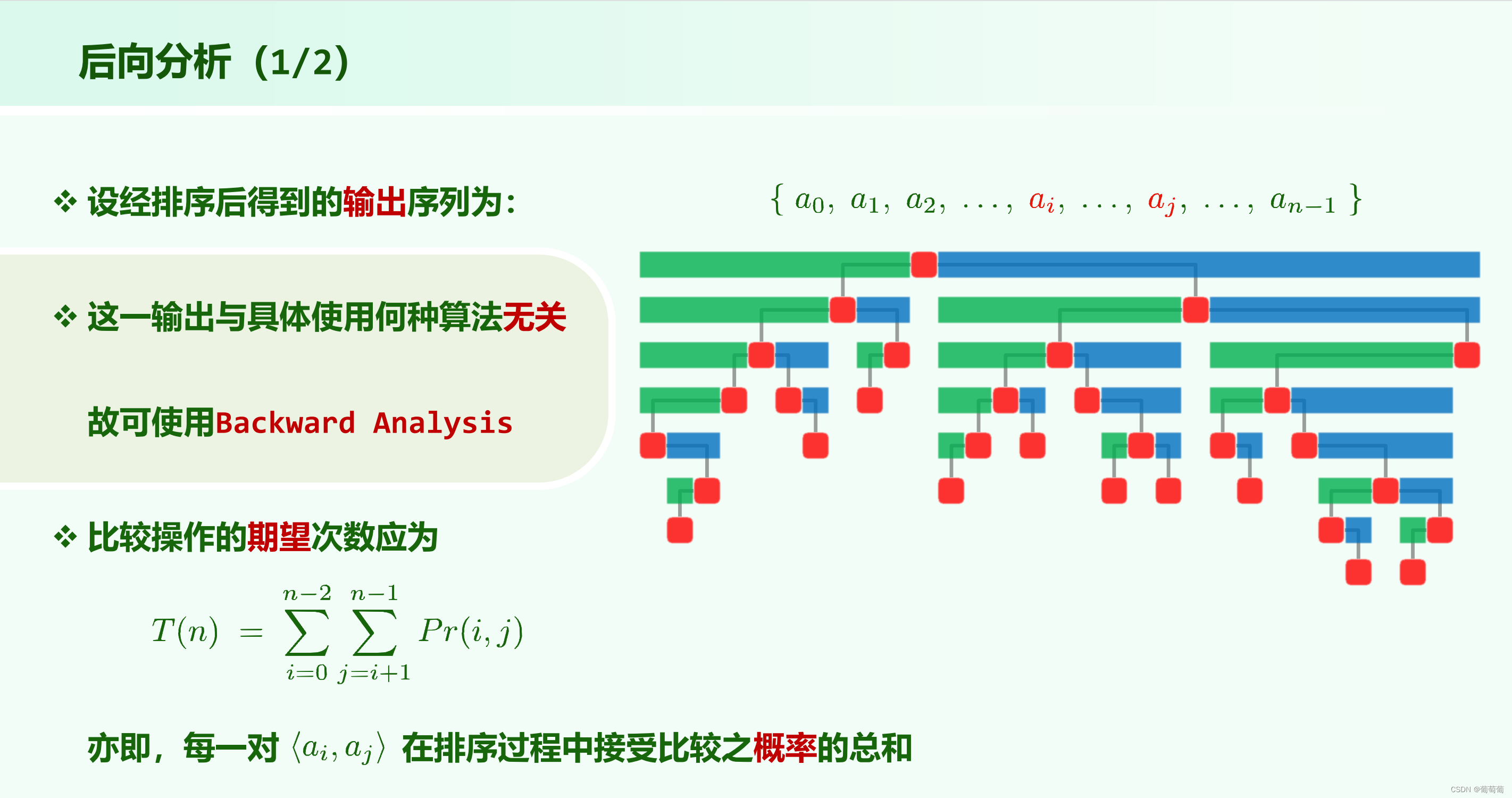
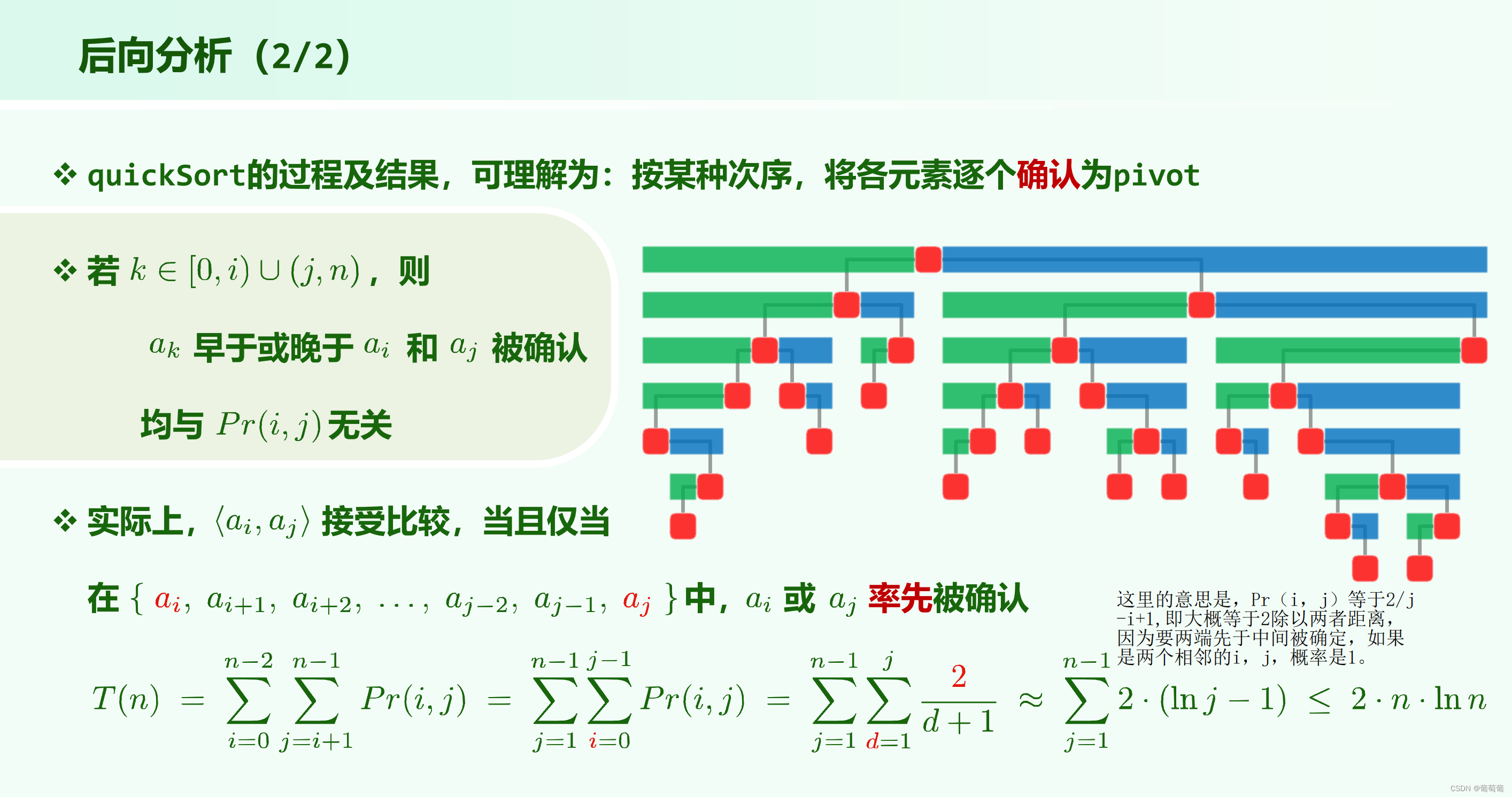 quicksort的期望在常数意义上更快，可能是因为这个被称为快速排序。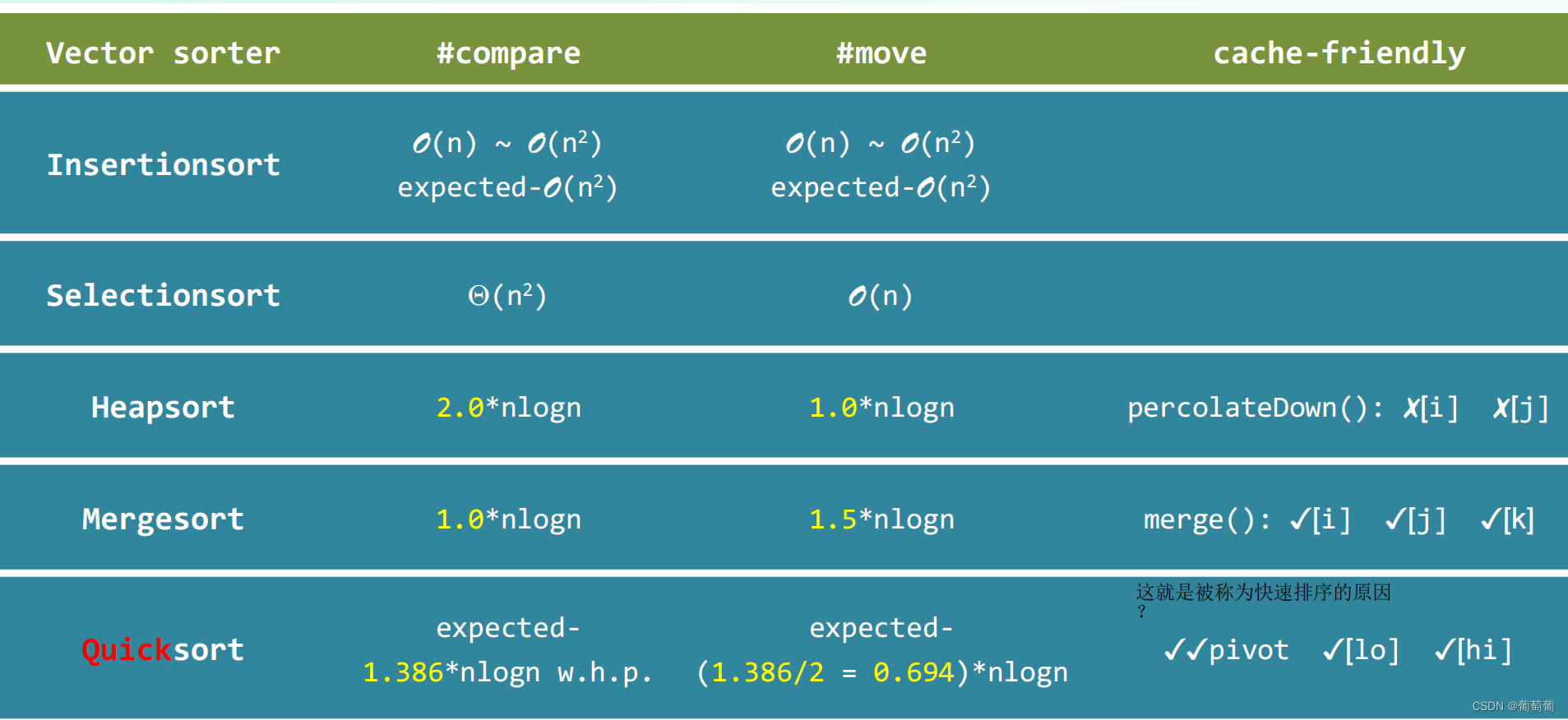

 找轴点的另一种实现：LGU，可以很好的实现稳定性，不会发生上面算法中次序颠倒，但是重复元素问题还是没有解决。

2.选取

众数：用下面的算法可以实现O（n）的复杂度

 中位数：

先考虑两个等长有序向量合并后的中位数选取。可以不用完全排序，因为实现完全排序的话大大超出了需求。下面trivialMedian( Vector<T>& S1, Rank lo1, Rank n1, Vector<T>& S2, Rank lo2, Rank n2 )就是用完全排序的方式求中位数，O（n+m），当m与n较小时可以调用。

因为 s2 的后缀一定是在总体中位数的后面， s1 前缀一定在总体中位数前面 （虽然不一定在总体排序中是连续的），总体中位数一定是去掉这两部分 的总序列的中位数。

迭代版：弄个循环一直取中比较就行了。

最后一行是把n2的前后(n2-n1-1)/2项去掉，因为这些值前面的一定是小于总体中位数，而后面的一定大于总体中位数，直接去掉后的新总体序列的中位数不发生变化。这保证n2长度大于等于n1，但是小于等于n1的两倍。

每次都能保证规模减少到原来2 /3，所以是O（logn）复杂度，再因为总规模取决于min（n1，n2），所以是O（logmin（n1，n2））

K—选取——quickselect（快速选取）：

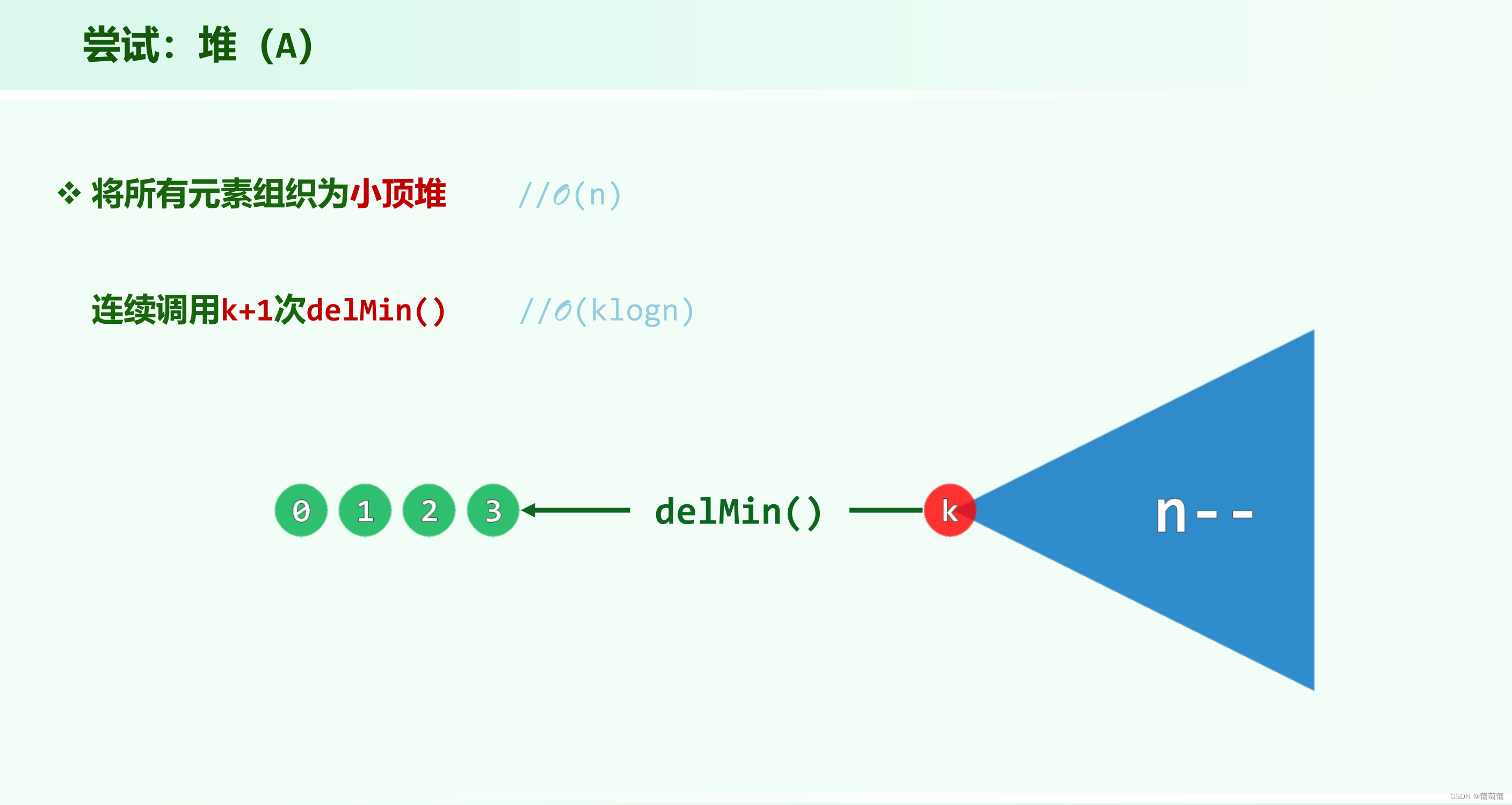
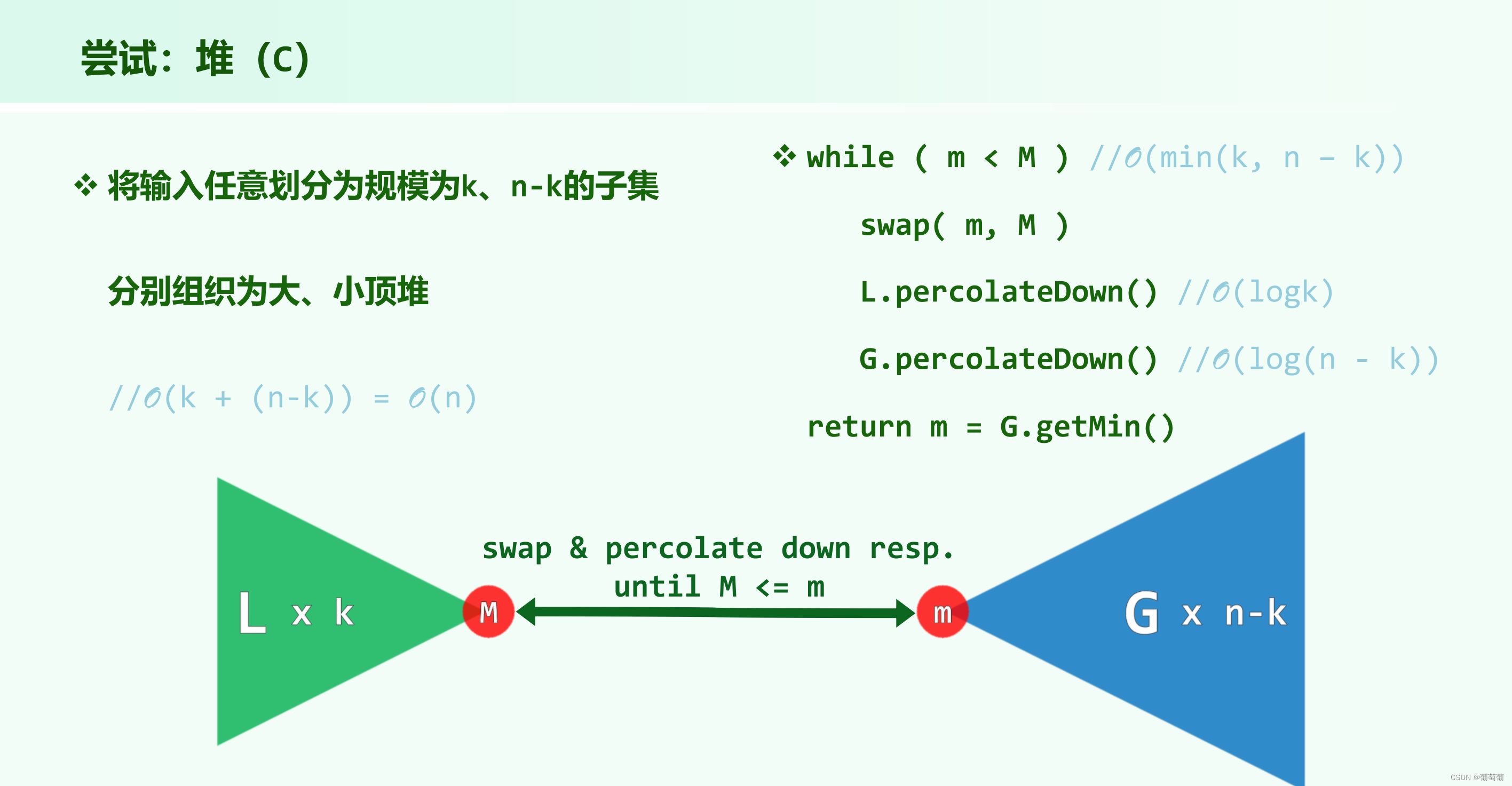
堆（B）正确性正确性分析：其实delmax出去的都要大于等于至少k+1个值

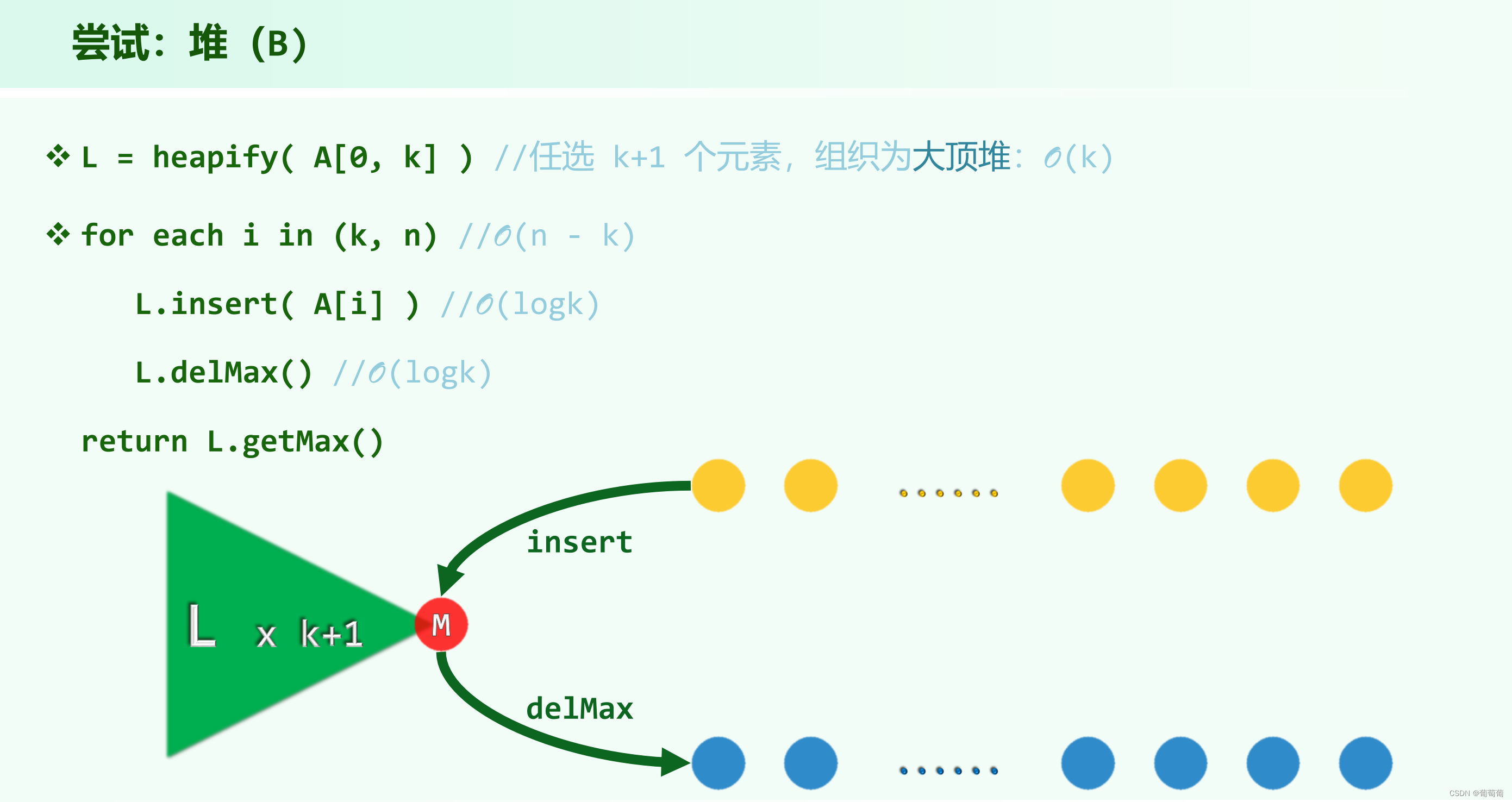
 循环次数不会超过min（k，n-k），因为极限情况就是k中没有一个是排在0-k的，需要k次交换，同理对n-k也是同样分析，所以要小于min（k，n-k）。

 其实就是做一次partition（找轴点），如果轴点正好等于k，那么返回；如果不相等，则缩小范围继续找轴点，直到k就是轴点。期望复杂度上第二个等式成立原因是当k在中间即找中位数时比较次数期望最多。（式子中的k是指不同轴点的选择）如何推导出O（ｎ）和４ｎ需要进一步证明。（有意思的是这个递推式和上面快速排序的递推式很相似，一个ｎｌｏｇｎ，一个ｎ，因为一个是把所有轴点都找出来，一个是找到一个特定轴点即可）

 K—选取——linｅａｒ　select：

注意中位数的中位数不一定是全体的中位数，但是至少是在总体１／４（图２的左下角）到３／４（图２的右上角）之间，所以至少能较少１／４的规模。所以这种情况最坏都是O（ｎ）的复杂度。如果在L区，肯定是排k位的数，在G区排k-L-E位

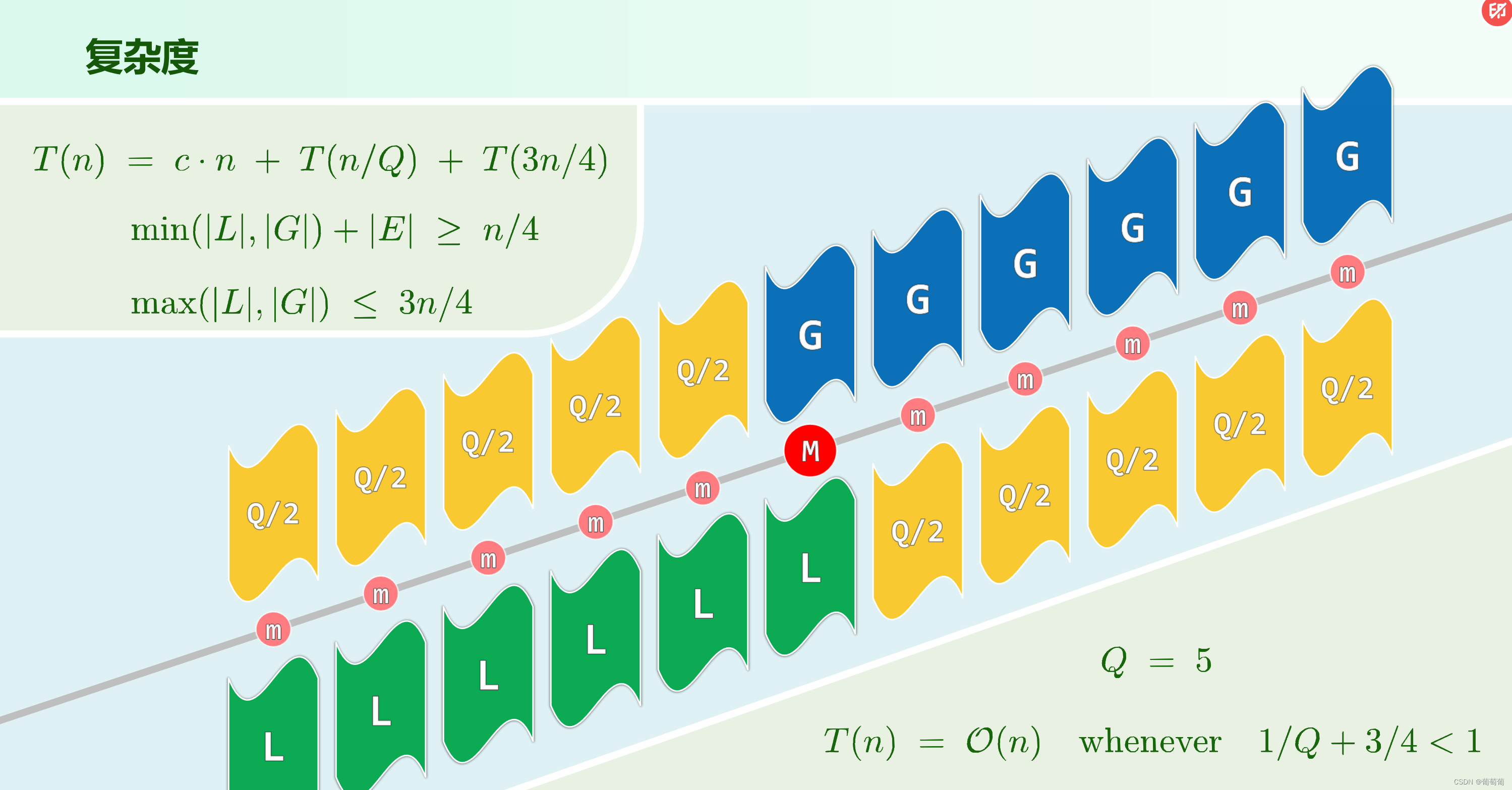
总结：众数、中位数、K－选取都能O（ｎ）实现。因为排序要求远大于选取，所以直觉上小于O（ｎｌｏｇｎ），且下限是O（ｎ）。

３.希尔排序（ｓｈｅｌｌ　ｓｏｒｔ）

ｈ（矩阵宽）确定后，矩阵与一维向量一一对应，可以用一维向量实现。（类似完全二叉堆的处理）

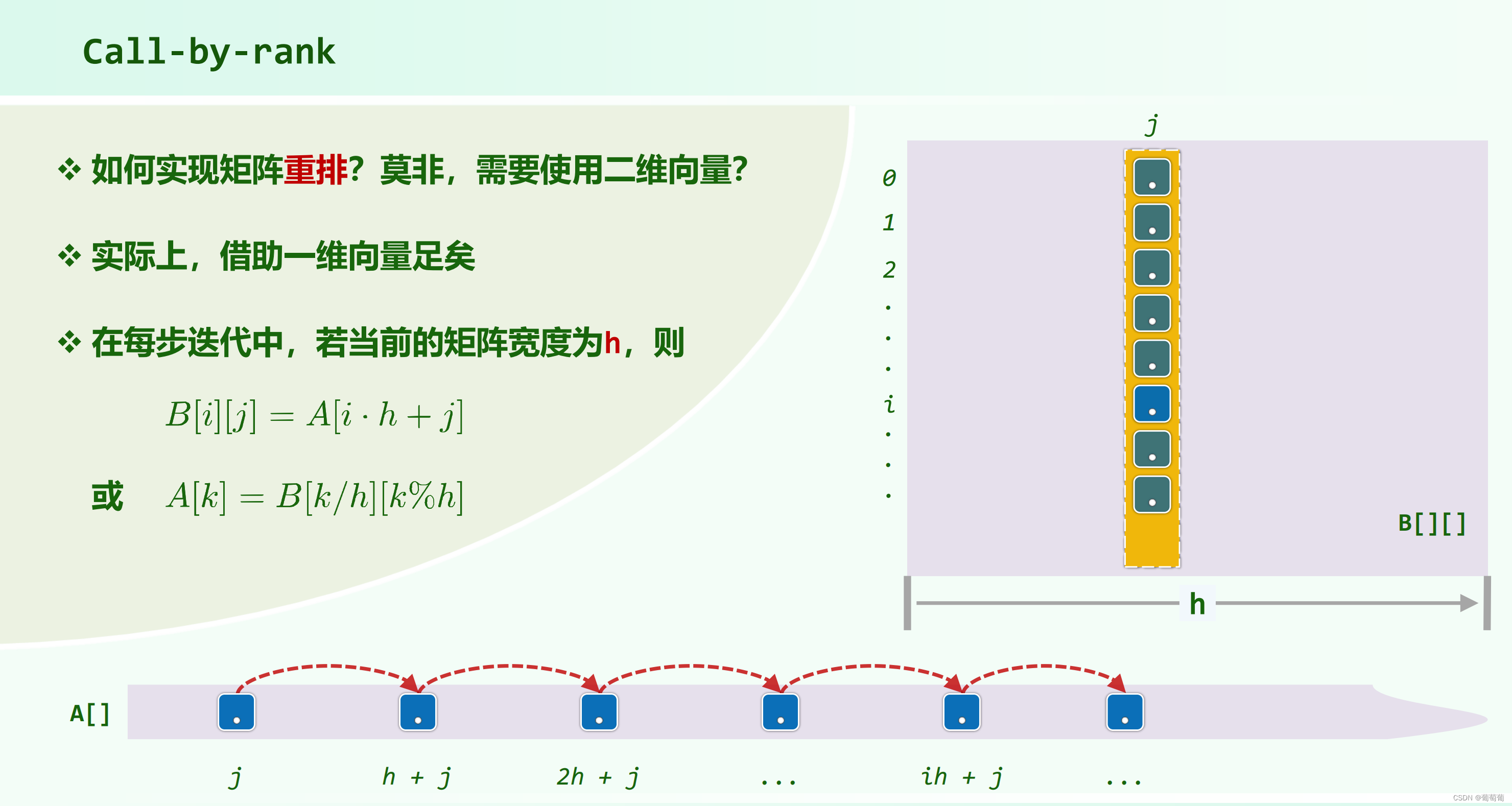
 可以看到ｊ是从第二行第一个开始循环，各列采用的是插入排序。

 Shell's Sequence：

直观上看造成下面情况的原因是每次排序奇数和偶数序列从来没有排到过一列进行比较。

 下面定理：两个互素的值的线性组合，所不能覆盖的值的最大值是ｇｈ－ｇ－ｈ，即大于这个数都可以被这两个数线性组合。（先不证明了）

Ｔｈｅｏｒｅｍ　K 下面定理：一个ｇ－ｏｒｄｅｒ的序列经过ｈ－ｓｏｒｔｉｎｇ之后还保持ｇ－ｏｒｄｅｒ，即ｈ－ｓｏｒｔｉｎｇ具有叠加性。第三张图表示的是第每一列有序后对行进行排序，列的有序性不会发生改变，证明可以假设每一行都使用冒泡排序，分析两行之间的冒泡排序，无论哪种情况，每一次交换或者不交换后列之间的次序性不会改变。

 

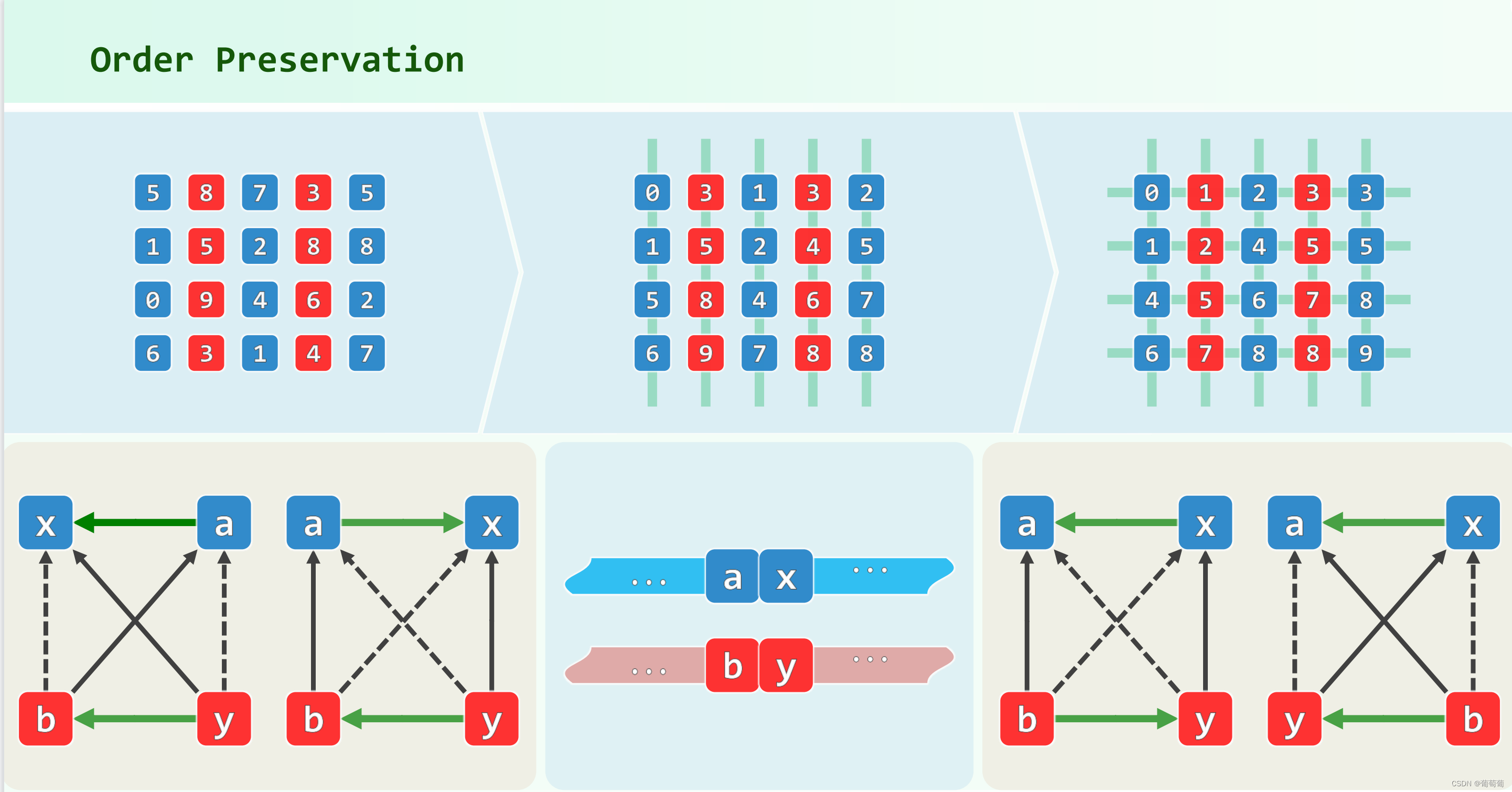
 这张图说明乱序的两个序列，有几对满足下面元素大于上面的元素，那么就至少有多少对下面的序列的最大的大于上面序列最小的。根据这个观察也可以证明上诉结论。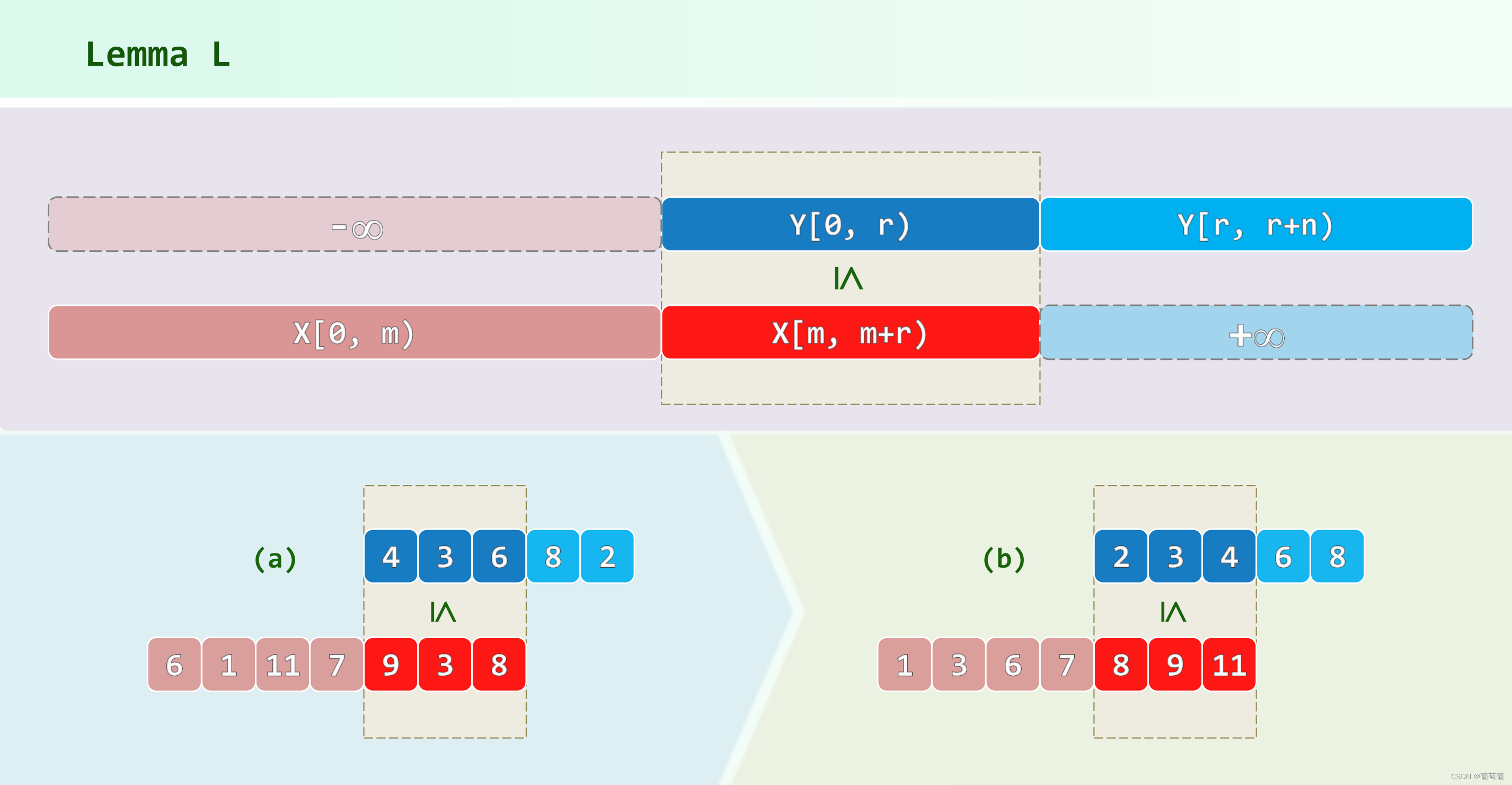

对于ｇ－ｏｒｄｅｒ和ｈ－ｏｒｄｅｒ的向量，两个元素距离如果相差超过X（ｇ，ｈ）（ｇｈ－ｇ－ｈ），表示一定可以被ｇ和ｈ线性表示，即可推出大小关系。也即在一个元素之前比它大的不超过X（ｇ，ｈ）个，即逆序对数目小于X（ｇ，ｈ）＊ｎ。

 PS序列：（Papernov & Stasevic, 1965 //also called Hibbard's sequence）

第一页中的g与h大于d，但是只是常数意义上的大于d，即O（d），且互素。上一页分析了如果是一个（g，h）-order的序列，逆序对数目不超过n*X（g，h）。也就是逆序对数目O（n*d^2），也即完全的对这个（g，h）-order的序列进行插入排序需要O（n*d^2）。但是如果只是是d-sorting不是完全的sorting，每一个元素最多只可能交换X（g，h）/d次（一个元素的前X（g，h）个元素，在分成d列后，在每一列中只是前X（g，h）/d个元素），所以总时间是O（X（g，h）/d*n），再因为g，h都O（d），所以总时间O（n*d）。

用这结论分析第四页，PS序列满足以上两个条件，即对于三个相邻元素来说，后两个元素互素且不会超过第一个元素太多（常数上*2-1），所以总是间O（n*d），d小于n^(1/2)，所以O（n^(3/2)）,结合第三页，PS序列每个h-sorting都是O（n^(3/2)）。时间上限是这么多，平均时间呢？n^(5/4）还未被证明？？ＰＳ序列每次减半，因此需要做ｌｏｇｎ次ｈ－ｓｏｒｔing，即总时间O（（n^(3/2)）＊ｌｏｇｎ）

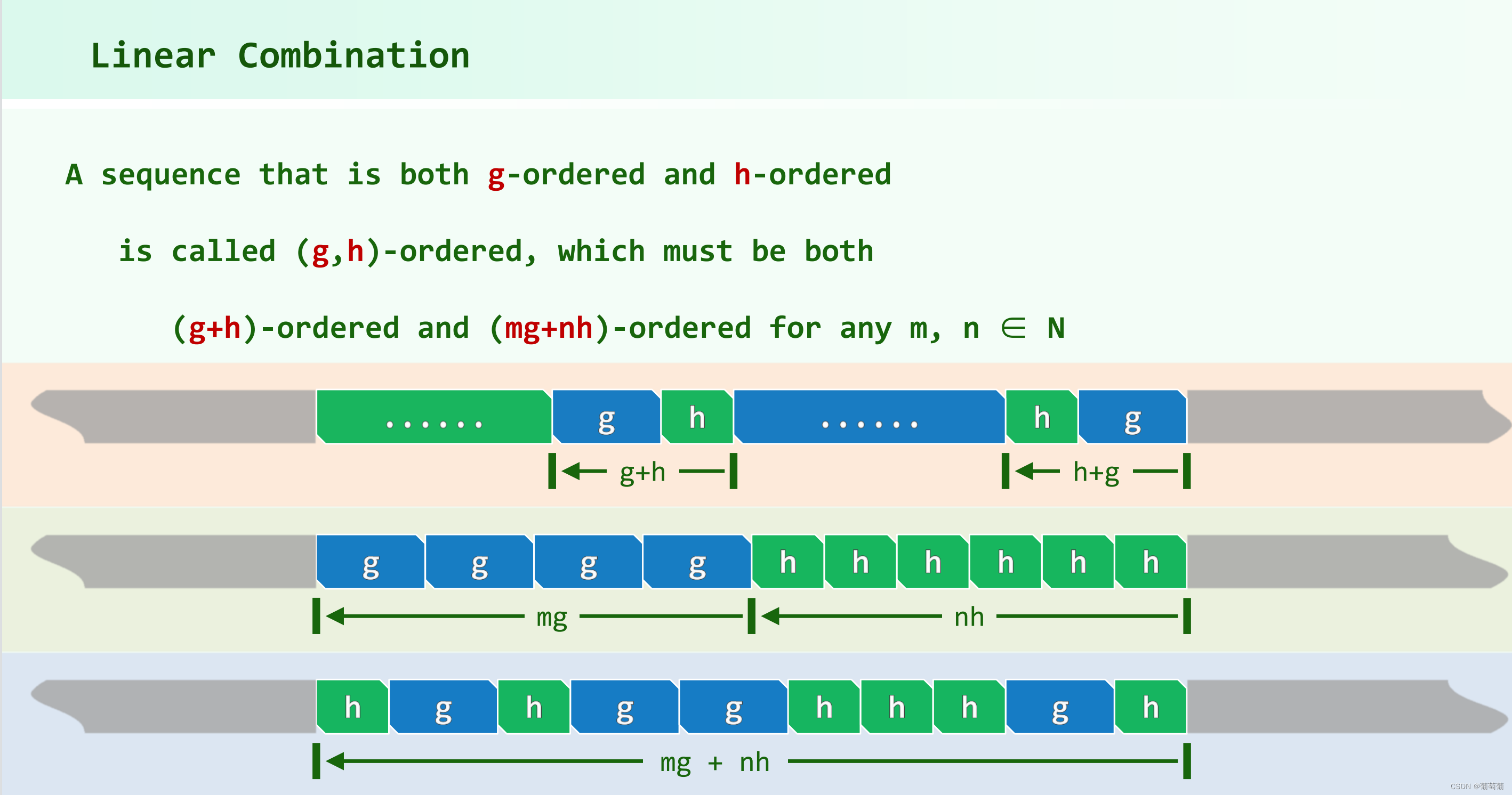
 小的ｏｒｄｅｒ的很可能直接推出大的ｏｒｄｅｒ（大的是小的的线性序列），大的变小需要再排序，但是可以根据前面的大的ｏｒｄｅｒ有可能减少排序的复杂度。一般的ｈ－ｓｏｒｔing需要ｎ＾２／ｈ的时间，但是如果小的和两个大的离得很近，也可以需要ｎｈ时间，两者哪个更小上限取哪个。（不管怎样，ｈ－ｓｏｒｔｉｎｇ的复杂度为逆序对数／ｈ，ｈ＝１时即就是逆序对数，而（ｇ，ｈ）－ｓｏｒｔｅｄ逆序对上限变为O（X（ｇ，ｈ）＊ｎ）ｇ、ｈ为素数，所以如果时ｇ、ｈ是O（１），那直接O（n）就能完成插入排序，下面的2，3就是如此）

Pratt序列：

ｎｏｔｅ　ｔｈａｔ　第二行举个例子：如果是PS序列，对于３＾２０次的规模，大概需要２０次ｈ－ｓｏｒｔｉｎｇ，但是对于Ｐｒａｔｔ序列，差不多需要１＋２＋３＋……２０次，即（ｌｏｇｎ）＾２.

如果一个序列是（２，３）－ｏｒｄｅｒｅｄ，只需O（ｎ）时间能将其变成完全有序。

分成ｈｋ列，每一列都是（2，3）-ordered，因此每个元素最多比较1次，因此O（n）的复杂度。因为每个hk前面都有2*hk以及3*hk-ordered，前面没有的因为hk趋近于n，所以复杂度也是O（n）。所以总的复杂度O（n*（logn）^2）。pratte序列和ps比，每次h-sorting时间上限降低，但是h-sorting次数增多。

Sedgewick序列：将pratte和ps序列结合一下？降低一些每一次h-sorting的上限，但是不会引起次数增加。

有没有nlogn的序列？