优先级队列

1.PQ数据结构提供了三个接口insert、getmax、deletemax，PQ和词典一样，接口都是要后续继承具体实现的，所以都是纯虚函数。用向量或者列表实现的话，三个接口总至少一个是O（n）的复杂度，用BBST的话，有点大材小用，BBST的搜索和删除都可以对任意关键码，而PQ只需对最大的关键码。

2.完全二叉堆是实现PQ的一种方式。完全二叉堆=完全二叉树+堆序性（父亲节点的值要大于孩子）（类比于BST=二叉树+左孩子小于父亲小于右孩子），因为完全二叉树（完全二叉树的叶子节点比内部节点多1或者相等，多1是当其为真二叉树时；相等是不为真二叉树时）可以用向量表示（一个向量可以和相应节点数量的完全二叉树完全对应），所以完全二叉堆可以是针对一个向量（和普通向量不同的是，在值上要求有堆序性）

实现：PQ_ComplHeap，继承PQ和向量。除了要重写PQ的三个接口外，还有三个比较重要的接口，分别是percolatedown(下滤)、percolateup（上滤）（想起了B树的上溢和下溢，但区别还是很大的）以及heapify （建堆，把一个普通的无序的向量变为具有堆序性，全序性是比堆序性更严格的一种排序，堆序性是更宽松的一种排序，可以把建堆看成宽松的排序），这几个接口都是为了保证向量的堆序性，上滤和下滤针对于插入、删除后的维护堆序性，建堆是直接对一个向量进行堆序排序。

template <typename T> Rank percolateDown( T* A, Rank n, Rank i ); //下滤

对数组A进行的第i项进行下滤，其中只考虑A中的前n项的堆序性。返回第i项数据新的秩（因为可能经过一系列交换导致秩改变）。

deletemax删除的时候将elem[0]与最末尾的元素调换，size--即将最大值删除，再对0进行下滤即可。复杂度O（logn）（复杂度期望值差不多也是logn，因为是最底层的与elem[0]交换，但是也不一定每次都是logn，也有可能会小于，所以比BBST稍微好些）

template <typename T> Rank percolateUp( T* A, Rank i ); //上滤

对数组A中的第i项进行上滤，上滤不需要考虑是A中的前几项，因为是向上走的，后面尾巴多长都不重要。

insert（）插入的时候对末尾节点进行一次上滤即可。复杂度O（logn）（注意这是最坏的情况是logn，不像BBST基本上是一定是logn，在这里最好的情况O（1）即可，所以如果按照期望来算这里的时间复杂度远远小于BBST）

查找getmax直接返回elem[0]即可。复杂度O（1）

template <typename T> void heapify( T* A, Rank n ); // Floyd建堆算法

对数组A的前n项进行堆序排序（即所谓的建堆）。

考虑两种算法思路，一种是自上而下的对每个位置进行上滤，正确性毋庸置疑，但是复杂度方面，注意到越往下，底层的位置越多（接近n/2）,而上滤的高度可能要是logn，所以时间复杂度是O（nlogn）。

另一种算法思路是自下而上的下滤，也能保证正确性，但是最底层位置最多的只要O（1）的时间，越往上虽然每个点所要的时间随高度增加，但是每一层点的数量在减少，所以求和只要O（n）的时间（堆排序本来就不是严格的排序，O（n）时间比O（nlogn）的时间更符合常识）

注意上面三个接口函数不仅仅可以用于compl-PQ,也可以直接对向量进行操作！！！(如下面的堆排序)

increase加完上滤即可，decrease减完下滤即可。remove只需与最后一个交换，如果值变大了就上滤，值变小了就下滤。

3. 堆排序

按照选择排序的思路，把最大的值选出来，放在最末。

利用上面的三个函数，先对向量heapify（），再把首元素和末元素交换，再堆前n-1项进行下滤（正好是末元素秩）。如此迭代，可以就地解决。其实对一个向量（已经是堆排序好的）一直执行deletemax，当向量size变成0时，再将原来size恢复，即是排序好的结果。（但是这有个前提，是向量数组要保持原状，而因为有缩容的机制，所以原来数组不会得以保持，所以这种方法实际不可行）

4.锦标赛树（做比较的方式像是进行锦标赛，以此得名）

胜者树：

叶子数为n的对应有两棵完全二叉树，其中一棵是真二叉树，另一棵不是真二叉树，现在约定叶子树为n的对应于真完全二叉树。如果是真完全二叉树，内部节点数比叶子数要小一，所以总的节点数为2n-1.可以用size为2n-1的向量实现该完全二叉树，其中叶节点为待排序的n个点（在向量的后n个）。前面的n-1个节点用来记录每一次比较的胜者，由此这样向量第一个值即为最小值。（较小得为胜者）。如此这样第一次对胜者树进行初始化需要进行n-1次比较，但之后如果想要找到第二小的值只要进行log（2n-1）次比较（即（O（logn），常数上每一层只需要比较一次，而完全二叉堆的deletemax的下滤需要两次比较），因为需要寻找第二小的只需将之前第一小的值改为max，然后沿着之前冠军的比赛路径再进行比较即可，不要所有再重新比较一遍。相似的，想要找第三小的，只需要沿着第二小成为冠军的比赛路径再比较一次。

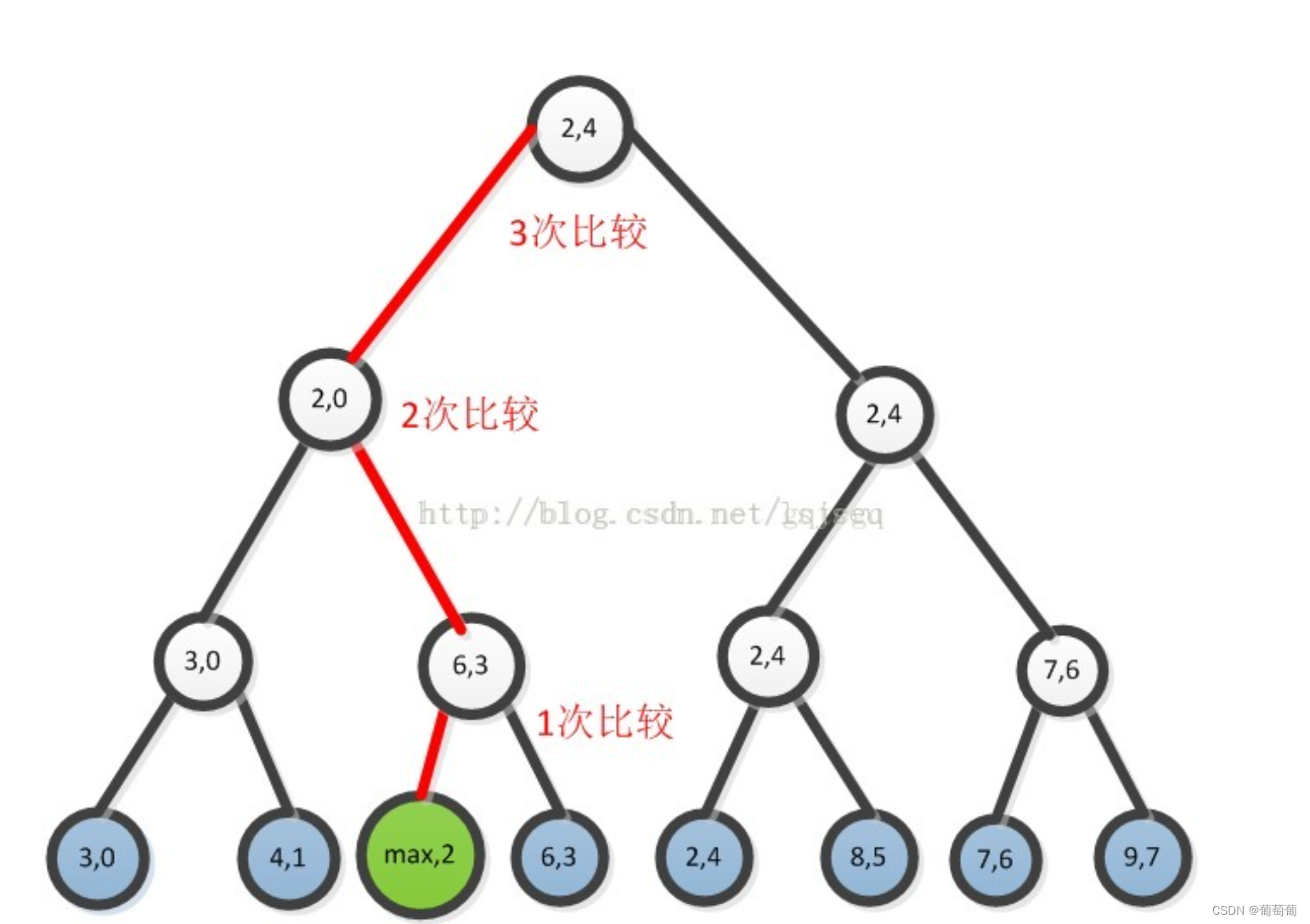
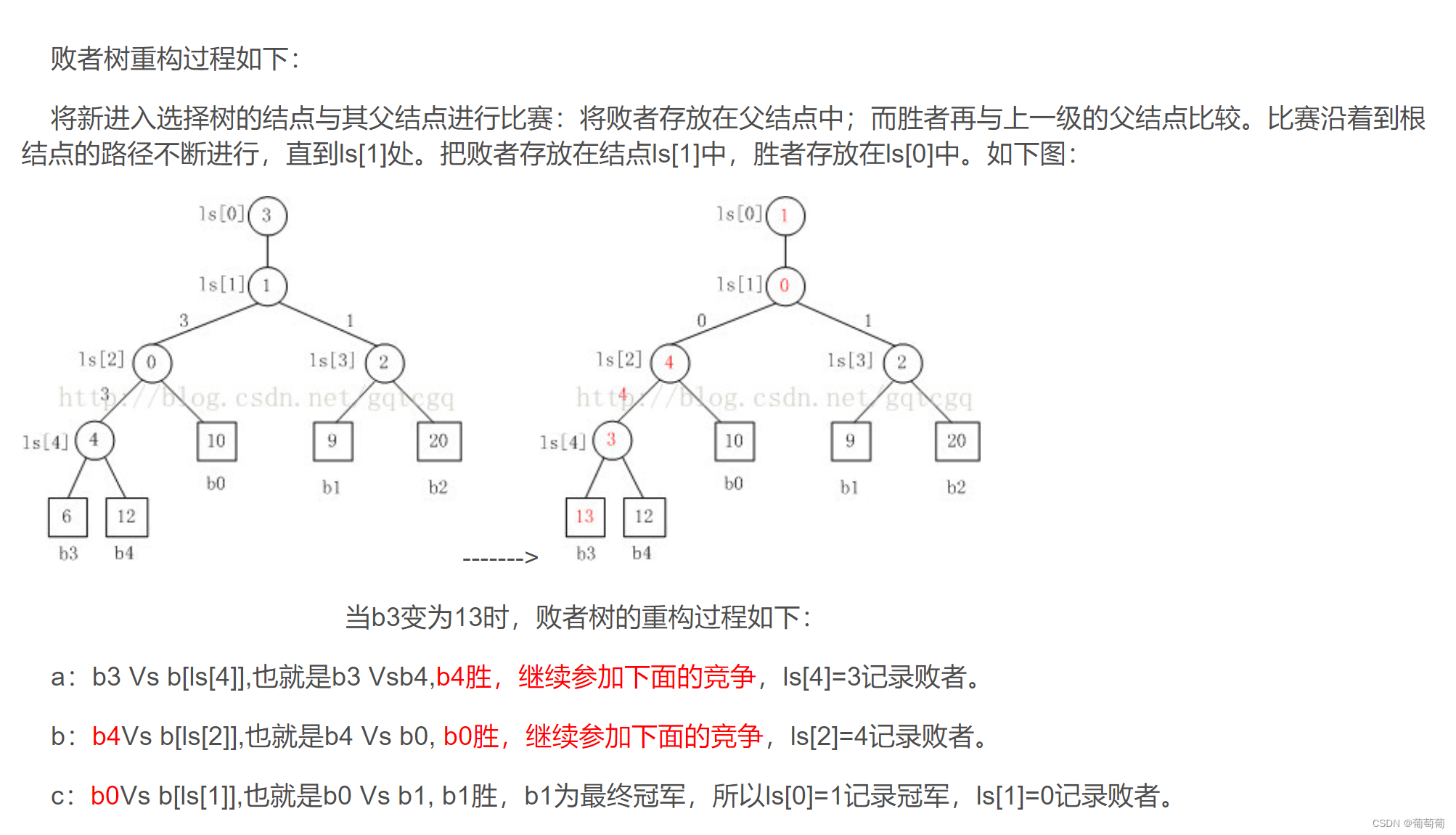
败者树：考虑胜者树在沿着前一次冠军诞生的比赛路径重新比较时需要访问沿途节点和其兄弟，而使用败者树可以只要对路径上的节点进行访问和比较即可。败者树在内部节点记录的是比较的失败者，具体实现可以像下面这样用一个数组表示内部节点，记录失败者编号，第一个记录冠军（根节点的父亲）。之后想要把上一次的冠军值变为max（或其他值）时，更新只需要访问路径上的节点即可，不需要访问兄弟。（12胜者树和败者树_锦标赛树和败者树_gqtcgq的博客-CSDN博客）

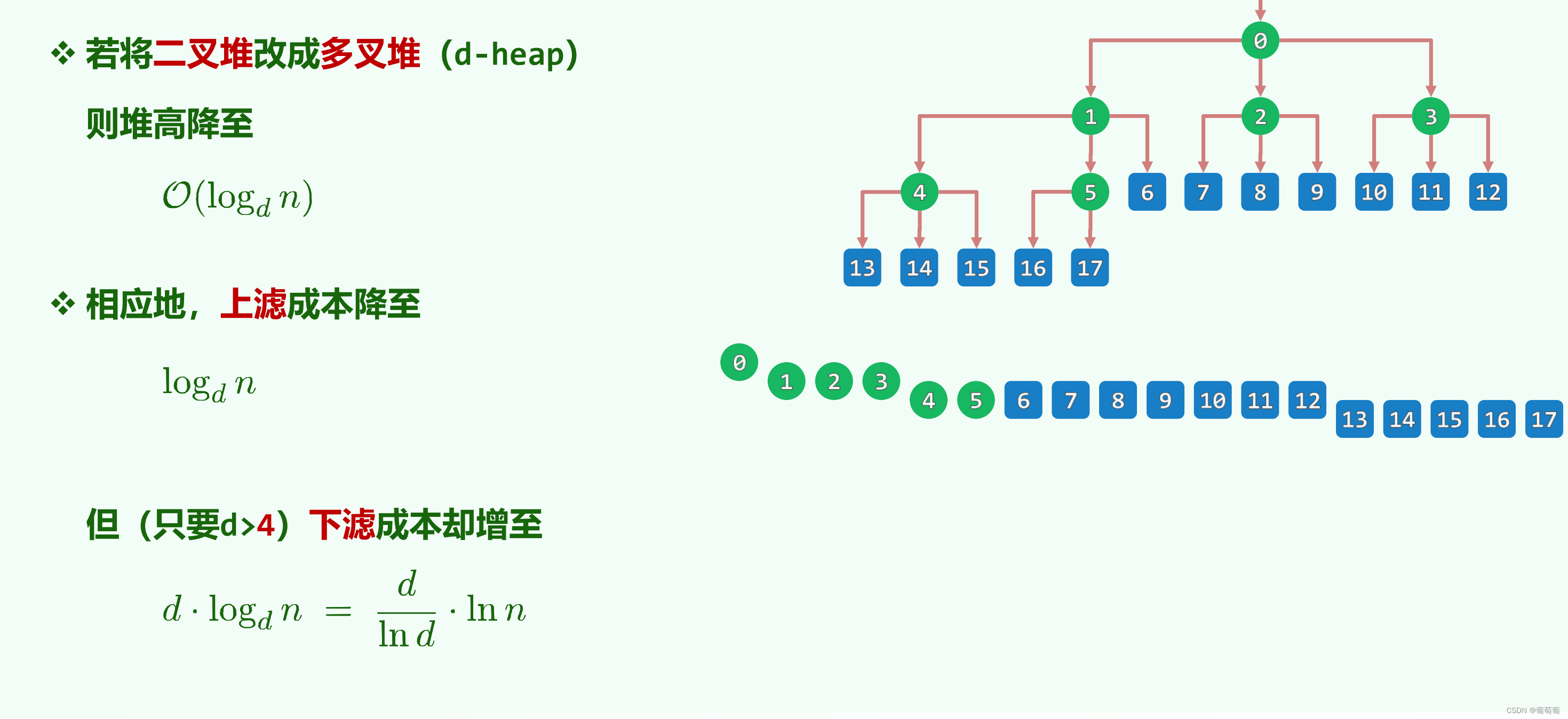
5.多叉堆

优先级队列与图的优先级搜索（PFS）联系：图中的点是以向量的形式组织，可以进行堆序化处理——O（n），取优先度最高deletemax——一次logn，n次O（nlogn），更新优先度increase——一次logn，e次O（elogn），所以总体复杂度O（（n+e）logn），普通的PFS是O（n^2）+O(n+e)，因此对于边少的稀疏图有较大的改善，对于边多的（O（n^2））稠密图则反而更差。所以有如下的结论：对于疏密程度不同的图采取不同的完全d叉树，可以改进时间复杂度。例如稠密图的d将采取n，而不是一个常数。

6.左式堆

堆合并：基于向量实现（完全二叉堆）的PQ，如果有两个堆排序好的向量，很难将其合并为一个。（堆是不是可以定义为具有堆序性的树，至少在逻辑上（（父亲的值大于孩子） ））

而基于二叉树（左式堆）实现的可以实现两个PQ的合并。（PQ_LeftHeap）

（基于BinTree不是BBST，bintree还是比较简单的数据结构，比列表稍微复杂一点）

类比于完全二叉堆=完全二叉树+堆序性（父亲的值大于孩子）  左式堆=左式树+堆序性

左式树：完全二叉树是特殊的二叉树，左式树也是特殊的二叉树。左式树需要满足下面的要求：每个节点左孩子的NPL要大于等于右孩子的NPL，NPL是存在节点中的一个属性值（和高度类似，AVL树要求每个节点的左右孩子的高度相差不超过1，有点类似），NPL是指到外部节点最近的距离。（NPL有一些性质，例如节点NPL值等于左右孩子NPL较小值+1，NPL值等于该节点的子树所包含的最大满树的高度，所以该树所包含的节点数大于等于于2^n+1 -1,内部节点数比外部节点数少1（真二叉树），所以内部节点数大于等于2^n -1，所以对于一棵有n个节点的树，其根节点的NPL一定是O（logn））因为左孩子的NPL值大于等于右孩子（左式树特点），所以节点NPL值一定比右孩子大1，于是沿着右侧链走NPL步一定可以到达外部节点，即右侧链长度等于NPL值，即O（logn）。

注意不像完全二叉树，给定n值对应可以有很多棵左式树。因此无法像完全二叉树那样用向量去描述左式树。

（PQ_LeftHeap）中最重要的接口就是merge，即将两个左式堆合并为一个。即将两棵具有堆序性的左式树合并成一棵具有堆序性的左式树。

template <typename T> BinNodePosi<T> merge( BinNodePosi<T> a, BinNodePosi<T> b )

接口实现有递归和迭代两种实现：

1、递归

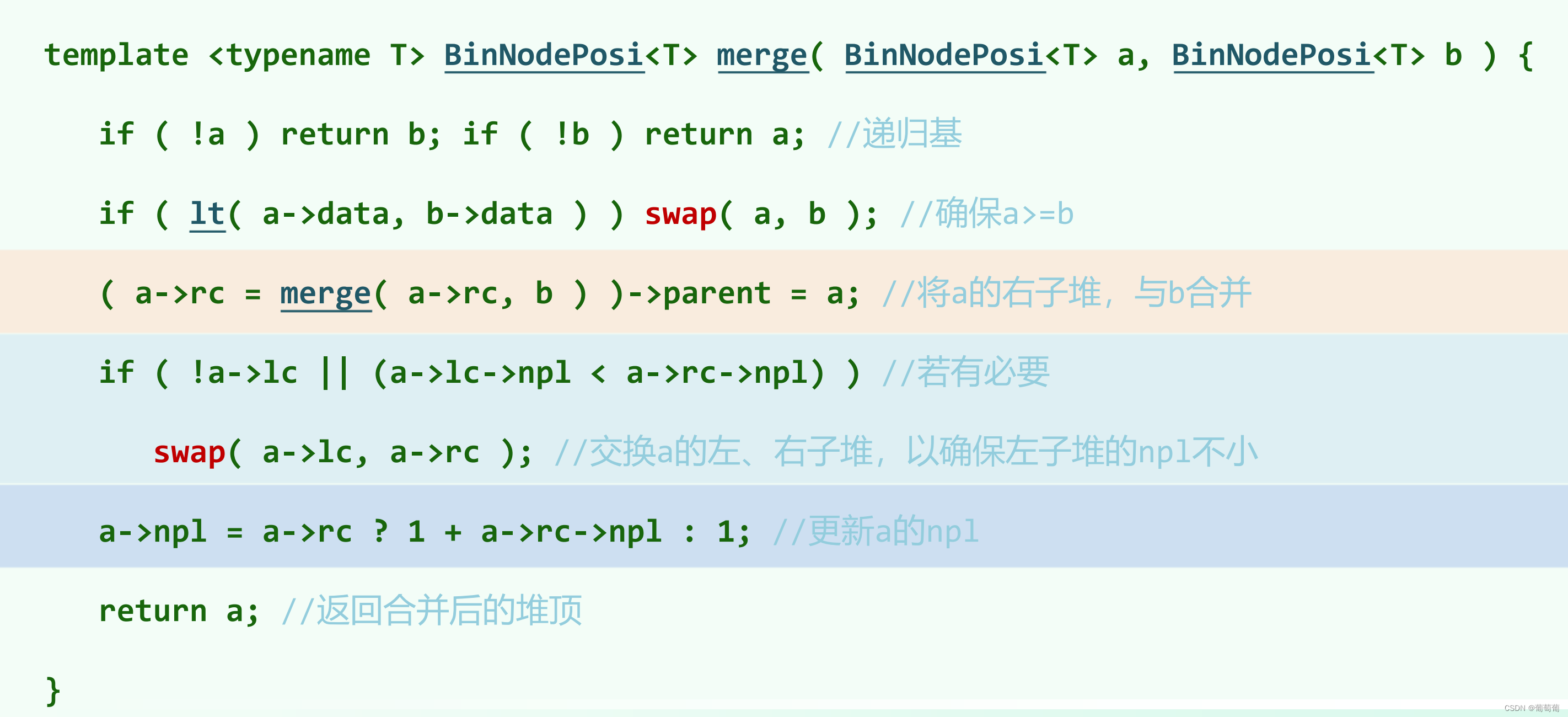
2、 迭代

 迭代和递归其实都主要对右侧链进行二路归并。（迭代第五行的a->data是不是 应该是a->rc->data）。复杂度是合并的两个左式堆的右侧链长度，即O（logn+logm）。

insert、getmax、deletemax：getmax只需返回当前左式堆（树）的根节点data（即是继承的二叉树，只不过这二叉树一出生就是左式堆，而且一直是左式堆，因为各种接口都是奔着左式堆去的，尤其是merge），insert只需调用merge（将新创建的节点看作一个左式堆）时间夫再度O（logn），deletemax直接将根节点删除，然后将左右子树当作两个左式堆进行merge，因为左式堆的子树依然是左式堆，所以两个子树的右侧链长度O（logn），所以总的时间复杂度O（logn）。

初始化：可以通过两个左式堆合并初始化，O（logn+logm）。

如何将一个向量初始化呢？类似于基于向量实现的heapify。可以一个个插入构造，如下文所示，O（nlogn）时间。可改进为Floyd建堆算法：可以先用heapify对向量进行完全二叉堆的堆排序，然后这棵完全二叉树一定是一棵左式树。将向量转为树结构即可。应该可以O（n）的时间。

PQ_LeftHeap( T* E, int n ) //批量构造：可改进为Floyd建堆算法

{ for ( int i = 0; i < n; i++ ) insert( E[i] ); }

7.优先级搜索树（PST）

暂略