CAD中下料排版、套料——贪心算法和遗传算法优劣对比——c#

       cad插件实现下料排版效果如下：

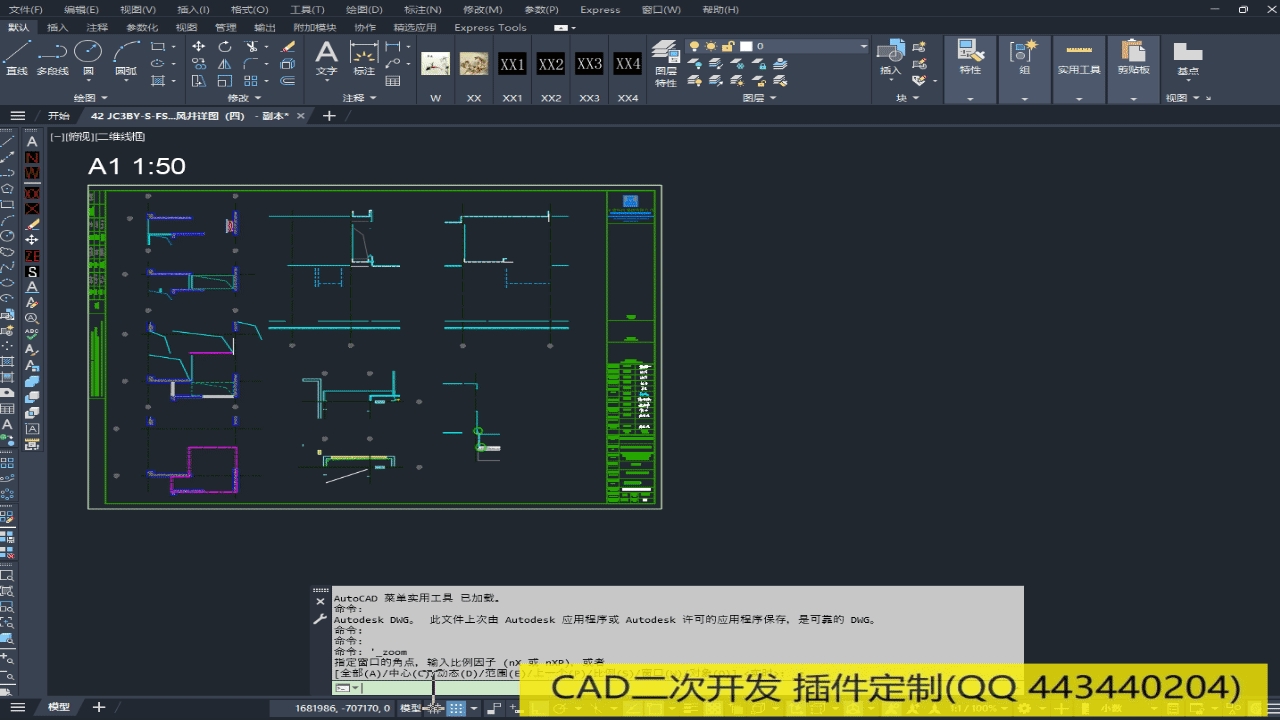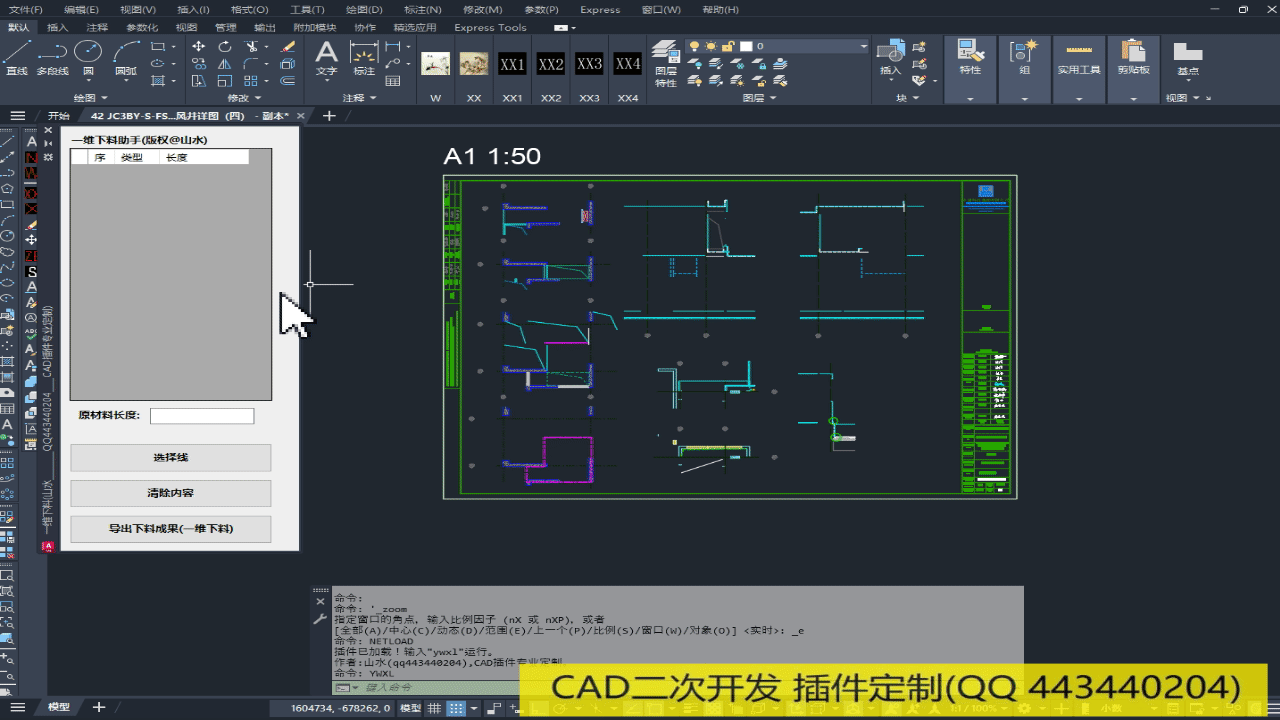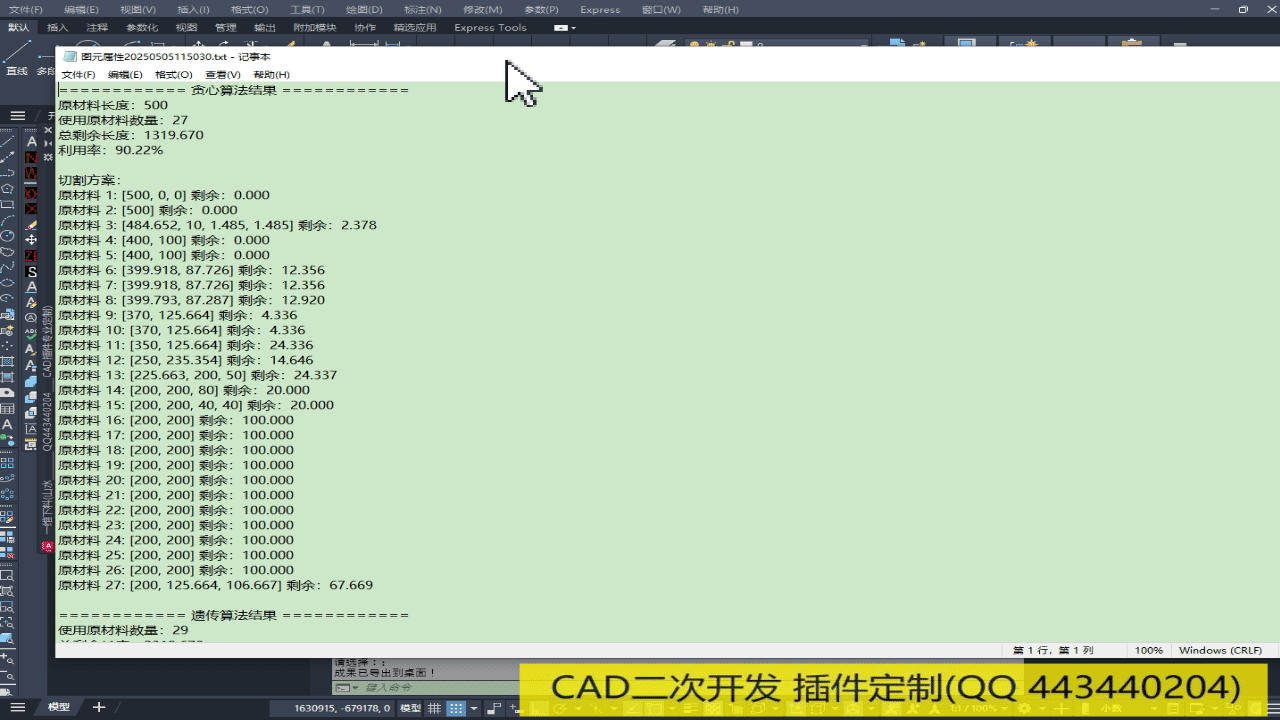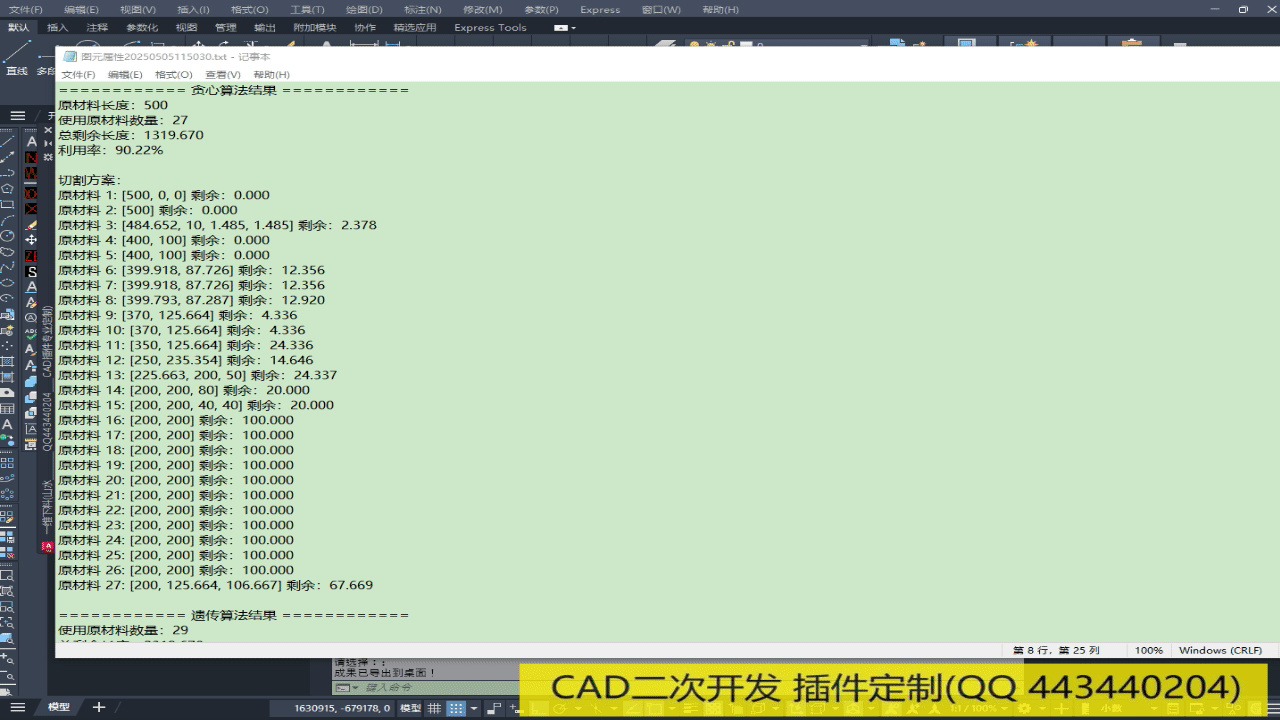
（使用方式：CAD命令行输入“netload”加载此插件，然后命令行输入：“ywxl”空格键即可。）

也可脱离cad环境，单独exe文件。

项目背景：某钢管厂的钢筋原材料为 55米，工作需要需切割 40 米（1段）、11 米（15 段）等 4 种规格 ，现用贪心算法和遗传算法两种算法进行计算：

第一局：{ 40, 1 },  { 11, 15 },{ 10, 1 }, { 5,1}，如何切割最省原材料？

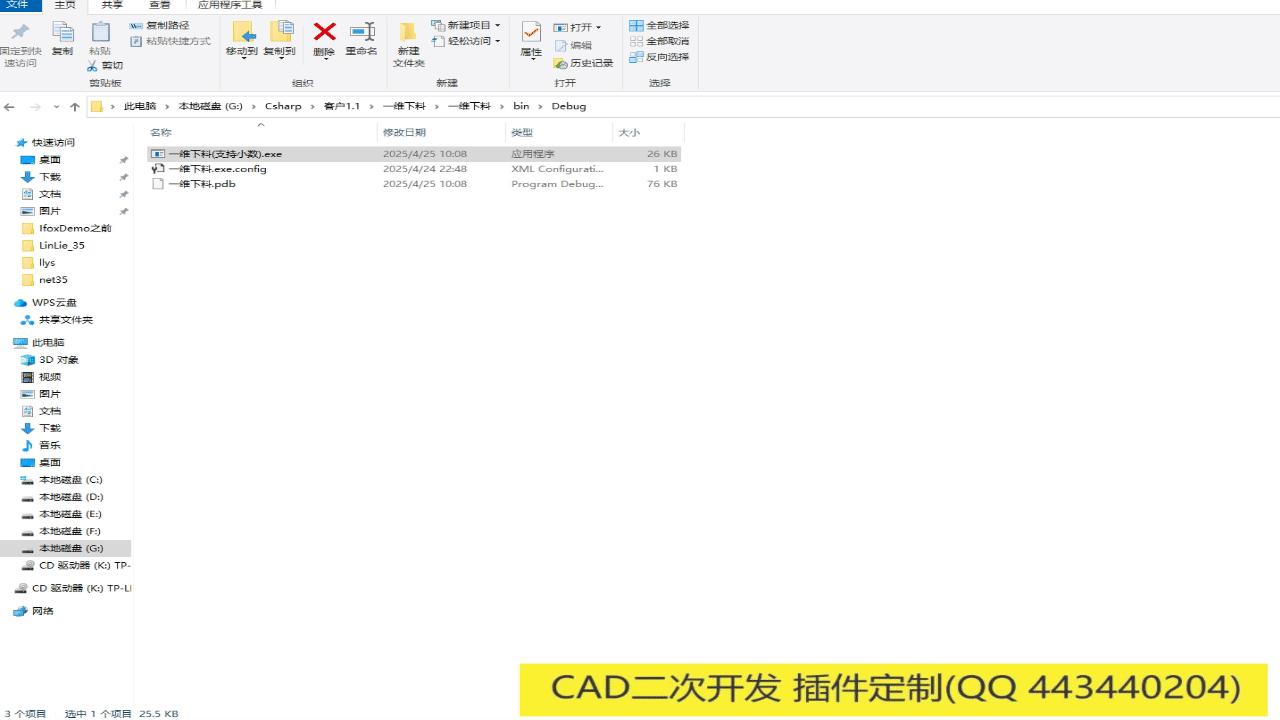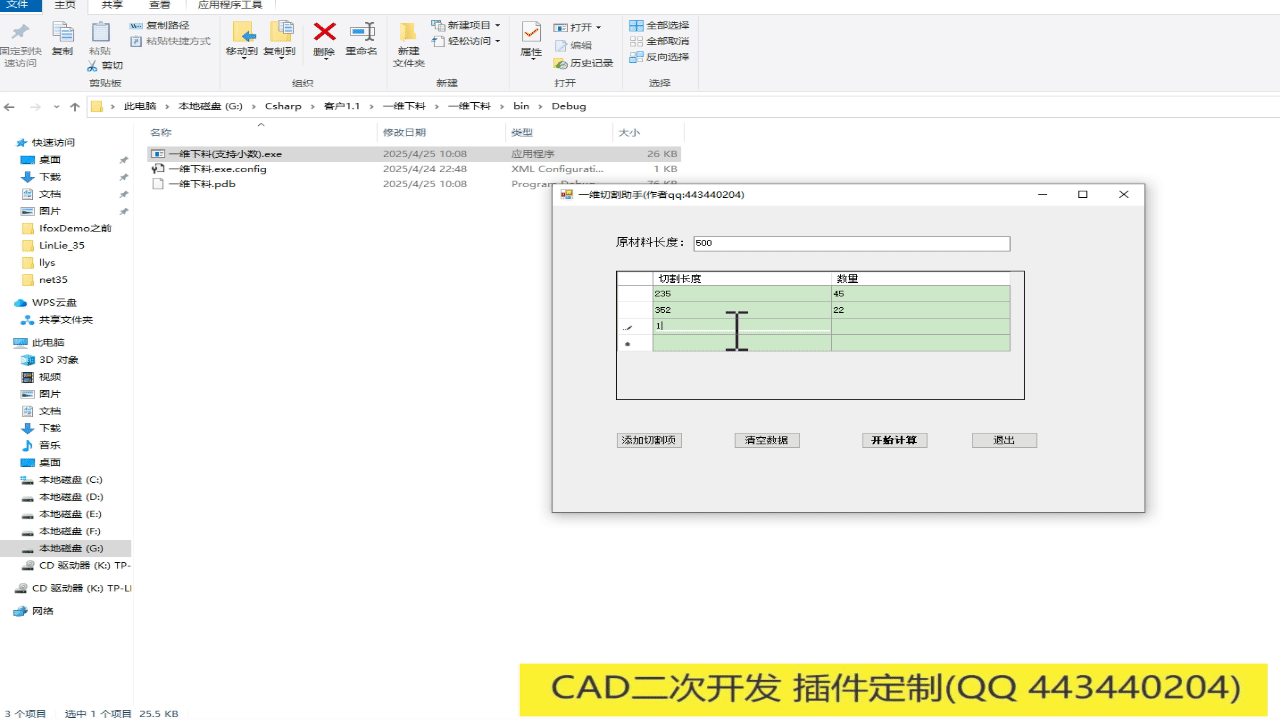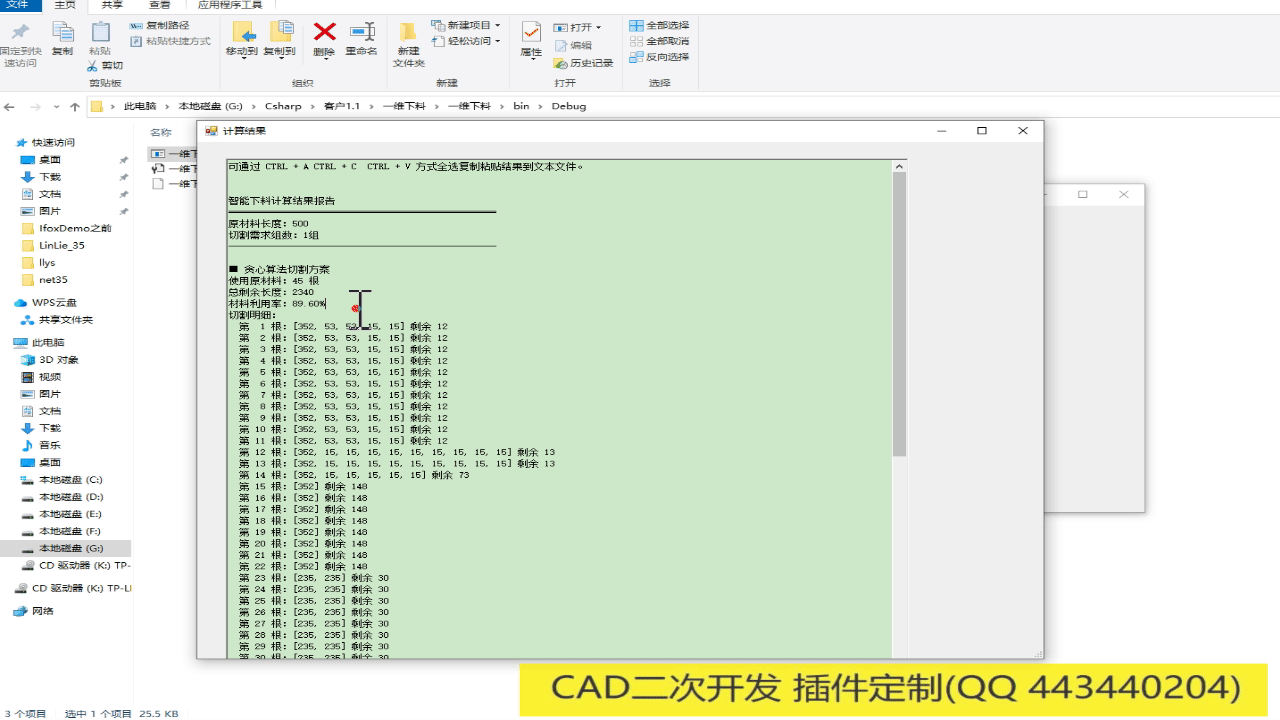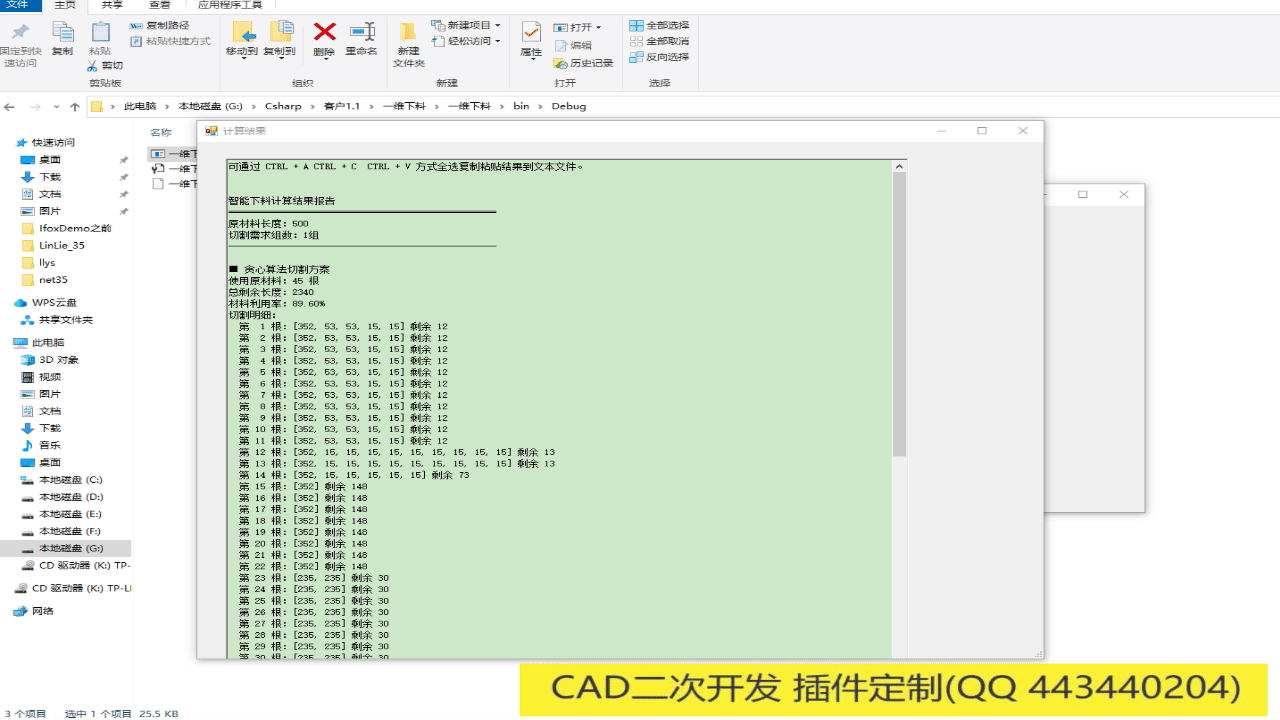
运行结果如下:

贪心算法切割方案：
原材料 1: [40, 11 ]剩余: 4 米
原材料 2: [11, 11, 11, 11, 11 ]剩余: 0 米
原材料 3: [11, 11, 11, 11, 11 ]剩余: 0 米
原材料 4: [11, 11, 11, 11, 10 ]剩余: 1 米
原材料 5: [5 ]剩余: 50 米
共需要5个原材料,总剩余: 55 米，贪心算法利用率: 80.00%
部分长度未切割完毕。
遗传算法切割方案：
原材料 1: [11, 11, 11, 11, 11] 剩余 0 米
原材料 2: [11, 11, 11, 11, 11] 剩余 0 米
原材料 3: [11, 11, 11, 11, 11] 剩余 0 米
原材料 4: [40, 10, 5] 剩余 0 米
遗传算法共需要4个原材料,总剩余: 0 米，遗传算法利用率: 100.00%

============ 方案对比 ============
贪心算法: 使用原材料 5 个，总剩余 55 米，利用率 80.00%
遗传算法: 使用原材料 4 个，总剩余 0 米，利用率 100.00%
最佳方案：遗传算法，利用率更高 100.00% > 80.00%

第一局，遗传算法获胜。

第二局，修改需求如下： 工作需要需切割 40 米（11段）、11 米（15 段）等 4 种规格  { 40, 11 },  { 11, 15 },{ 10, 11}, { 5,11}

运算结果：

贪心算法切割方案：
原材料 1: [40, 11 ]剩余: 4 米
原材料 2: [40, 11 ]剩余: 4 米
原材料 3: [40, 11 ]剩余: 4 米
原材料 4: [40, 11 ]剩余: 4 米
原材料 5: [40, 11 ]剩余: 4 米
原材料 6: [40, 11 ]剩余: 4 米
原材料 7: [40, 11 ]剩余: 4 米
原材料 8: [40, 11 ]剩余: 4 米
原材料 9: [40, 11 ]剩余: 4 米
原材料 10: [40, 11 ]剩余: 4 米
原材料 11: [40, 11 ]剩余: 4 米
原材料 12: [11, 11, 11, 11, 10 ]剩余: 1 米
原材料 13: [10, 10, 10, 10, 10, 5 ]剩余: 0 米
原材料 14: [10, 10, 10, 10, 10, 5 ]剩余: 0 米
原材料 15: [5, 5, 5, 5, 5, 5, 5, 5, 5 ]剩余: 10 米
共需要15个原材料,总剩余: 55 米，贪心算法利用率: 93.33%
部分长度未切割完毕。
遗传算法切割方案：
原材料 1: [40] 剩余 15 米
原材料 2: [40] 剩余 15 米
原材料 3: [40] 剩余 15 米
原材料 4: [40] 剩余 15 米
原材料 5: [40] 剩余 15 米
原材料 6: [40] 剩余 15 米
原材料 7: [40] 剩余 15 米
原材料 8: [40] 剩余 15 米
原材料 9: [40] 剩余 15 米
原材料 10: [40] 剩余 15 米
原材料 11: [40, 11] 剩余 4 米
原材料 12: [11, 11, 11, 11, 11] 剩余 0 米
原材料 13: [11, 11, 11, 11, 11] 剩余 0 米
原材料 14: [11, 11, 11, 11, 10] 剩余 1 米
原材料 15: [10, 10, 10, 10, 10] 剩余 5 米
原材料 16: [10, 10, 10, 10, 10, 5] 剩余 0 米
原材料 17: [5, 5, 5, 5, 5, 5, 5, 5, 5, 5] 剩余 5 米
遗传算法共需要17个原材料,总剩余: 165 米，遗传算法利用率: 82.35%
============ 方案对比 ============
贪心算法: 使用原材料 15 个，总剩余 55 米，利用率 93.33%
遗传算法: 使用原材料 17 个，总剩余 165 米，利用率 82.35%
最佳方案：贪心算法，利用率更高 93.33% > 82.35%

第二局，贪心算法获胜

然而，最佳答案为 40米 +10米 +5 米分一组，需要11根原材料。11米的单独一组，11*15/55=3根原材料。11+3=14，共需14个原材料，利用率100%。由此可见，每种算法各有优缺点，不一定是最优解。