RBM and NADE TO Collaborative Filtering

RBM and NADE TO Collaborative Filtering

最近在看深度学习在推荐算法上应用，本篇是hulu公司同事的ICML的文章A Neural Autoregressive Approach to Collaborative Filtering,介绍了利用NADE进行电影推荐的方法，在NETFX的数据集上取得了不错的结果，本文主要是学习和记录笔记，学习NADE-CF，并记录所涉及的一些算法，供后续查看方便。

RBM

RBM主要参考受限波尔兹曼机简介-张春霞,同时也参考核复制了博客的很多内容 深度学习读书笔记之RBM（限制波尔兹曼机)。在这里主要简介RBM涉及的几个计算公式，方便后边实现的理解。

能量函数

能量函数。随机神经网络是根植于统计力学的。受统计力学中能量泛函的启发，引入了能量函数。能量函数是描述整个系统状态的一种测度。系统越有序或者概率分布越集中，系统的能量越小。反之，系统越无序或者概率分布越趋于均匀分布，则系统的能量越大。能量函数的最小值，对应于系统的最稳定状态。

$$E(v,h|\theta)=-\sum_{i=0}^{n}{a_iv_i}-\sum_{j=0}^{m}{b_jh_j}-\sum_{i=0}^{n}\sum_{j=0}^{m}{{v_i}W_{ij}h_j}$$
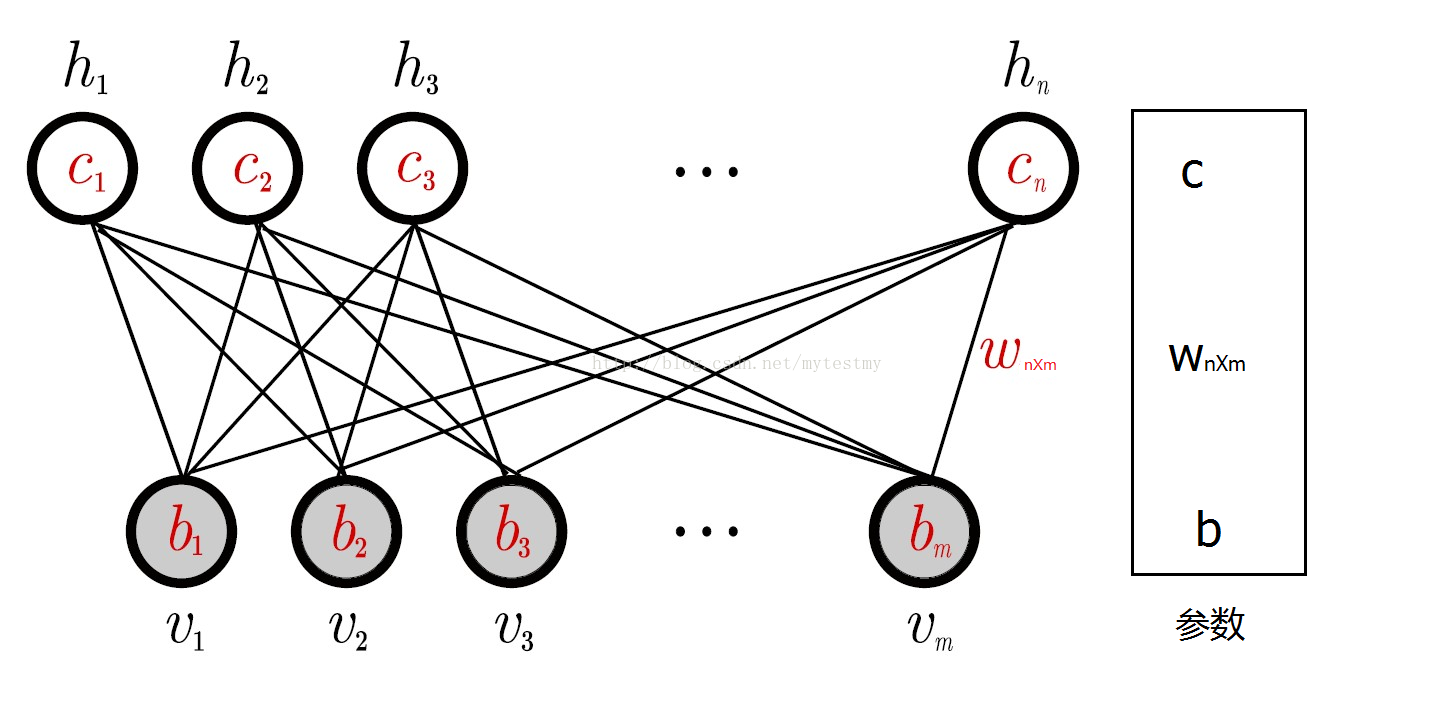
其中， $a_i$和 $b_j$为偏置， $v_i$为可见层， $h_j$为隐藏层。

似然函数

有了能量函数，定义可视节点和隐藏层的联合概率分布。

$$p(v,h|\theta) = \frac{e^{-{E(v,h|\theta)}}} {Z(\theta)},$$
$$Z(\theta)=\sum_{v,h} {e^{-{E(v,h|\theta)}}}$$
由联合概率可以得到观测数据 $v$的概率分布$p(v|\theta)$，也成为似然函数
$$p(v|\theta) = -\frac{1}{Z(\theta)}\sum_h{e^{-{E(v,h|\theta)}}}$$
同理，可以获得每个节点的激发函数,RBN层内节点不连接，同一层各节点独立分布。
$$p(v_i=1|h,\theta) = \sigma(a_i+\sum_j{h_j W_{ij}})$$
$$p(h_i=1|v,\theta) = \sigma(b_i+\sum_i{v_i W_{ij}})$$

对比散度RBM参数训练

学习RBM的任务是求出参数$\theta$的值, 以拟合给定的训练数据。 参数$\theta$可以通过最大
化RBM在训练集昨假设包含T个样本昩上的对数似然函数学习得到, 即

$$\Theta^* = {arg\max}_{\theta}({\xi(\theta)}) = {arg\max}_{\theta}{\sum_{t=1}^{T} {logp(v^{t}|\theta)}}$$
Hiton提出了RBM的一个快速学习算法, 即对比散度(Contrastive Divergence)。与吉布斯采样不同, CD指出当使用训练数据初始化 $v_0$ 时, 我们仅需要使用k步吉布斯采样便可以得到足够好的近似。在CD算法一开始， 可见单元的状态被设置成一个训练样本，并利用式 $p(h|v,\theta)$计算所有隐层单元的二值状态。在所有隐层单元的状态确定之后,来确定第i个可见单元 $v_i$取值为1的概率,进而产生可见层的一个重构。

• 输入:一个训练样本$m_0$,隐层单元个数$m$,学习率$$,最大训练周期$T$.
• 输出:连接权重矩阵W、可见层的偏置向量a、隐层的偏置向量b.
• 训练阶段:
  
  • 初始化可见层单元的初始状态$v1=x_0;W a$和b为随机的较小数值。
  • For t=1,2…T
  • For j=1,2..m(对所有隐层单元)
    
    • 计算隐层节点分布$p(h_{1j}=1|v_1)$,$p(h_{1j}=1|v_1) = \sigma(b_j+\sum_i{v_{1i} W_{ij}})$
    • 计算隐层节点$h_{1j}$,从条件$p(h_{1j}=1|v_1)$中抽样$h_{1j}= {0,1}$,具体$h_{1j}=p(h_{1j}=1|v_1)>Rand(numHidden+1)? 1:0$
  • EndFor
  • For i=1,2,….,n(对所有可见层单元)
    
    • 计算$p(v_{2i}=1|h_1)$,$p(v_{2i}=1|h_1) = \sigma(a_i+\sum_j{h_j W_{ij}})$
    • 计算节点$v_{1i}$,从条件$p(v_{1j}=1|h_1)$中抽样$v_{1i}= {0,1}$,具体$v_{1i}=p(v_{1i}=1|h_1)$(参考下文中代码实现)
  • EndFor
  • For 1,2,…,m（对所有隐层单元）
    
    • 计算隐层节点分布$p(h_{2j}=1|v_2)$,$p(h_{2j}=1|v_2) = \sigma(b_j+\sum_i{v_{2i} W_{ij}})$
  • EndFor
  • 参数更新(根据上文的导数可以求得)
    
    • $W=W+(p(h_{1}=1|v_1)v^T_1-p(h_{2}=1|v_2))v^T_2$
    • $a=a+(v_1-v_2)$
    • $b=b+(p(h_{1}=1|v_1)-p(h_{2}=1|v_2))$

  python code 参考训练过程

  
   def train(self, data, max_epochs = 1000):
      """
      Train the machine.
      Parameters
      ----------
      data: A matrix where each row is a training example consisting of the states of visible units.    
      """
  
      num_examples = data.shape[0]
  
      # Insert bias units of 1 into the first column.
      data = np.insert(data, 0, 1, axis = 1)
  
      for epoch in range(max_epochs):      
        # Clamp to the data and sample from the hidden units. 
        # (This is the "positive CD phase", aka the reality phase.)
        pos_hidden_activations = np.dot(data, self.weights)      
        pos_hidden_probs = self._logistic(pos_hidden_activations)
        pos_hidden_states = pos_hidden_probs > np.random.rand(num_examples, self.num_hidden + 1)
        # Note that we're using the activation *probabilities* of the hidden states, not the hidden states       
        # themselves, when computing associations. We could also use the states; see section 3 of Hinton's 
        # "A Practical Guide to Training Restricted Boltzmann Machines" for more.
        pos_associations = np.dot(data.T, pos_hidden_probs)
  
        # Reconstruct the visible units and sample again from the hidden units.
        # (This is the "negative CD phase", aka the daydreaming phase.)
        neg_visible_activations = np.dot(pos_hidden_states, self.weights.T)
        neg_visible_probs = self._logistic(neg_visible_activations)
        neg_visible_probs[:,0] = 1 # Fix the bias unit.
        neg_hidden_activations = np.dot(neg_visible_probs, self.weights)
        neg_hidden_probs = self._logistic(neg_hidden_activations)
        # Note, again, that we're using the activation *probabilities* when computing associations, not the states 
        # themselves.
        neg_associations = np.dot(neg_visible_probs.T, neg_hidden_probs)
  
        # Update weights.
        self.weights += self.learning_rate * ((pos_associations - neg_associations) / num_examples)
  
        error = np.sum((data - neg_visible_probs) ** 2)
        print("Epoch %s: error is %s" % (epoch, error))

  如果详细的了解过程，可以看一下github上代码Restricted Boltzmann Machines in Python

  RBM-CF

  有了以上对RBM的介绍和认识，接下来的RBM-CF的原理就很好理解了。Restricted Boltzmann Machines in Python是Hinton大牛在2007ICML上提出的,在netfext上也取得了不错的效果。下面就详细的介绍一下算法。
  
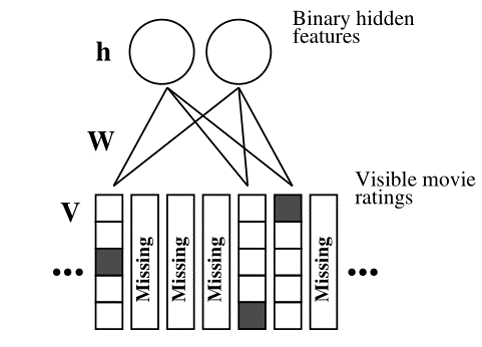
  如图所示，RBM-CF是一个标准的RBM。其中V是用户对电影的评分（如图是5个级别）.可见层为用户对电影的评分向量，隐层为隐向量。

  能量函数和似然函数

  $$E(v,h|\theta)=-\sum_{i=1}^{n}{\sum_{k=1}^{K}{a_iv^k_i}}-\sum_{j=1}^{m}{b_jh_j}-\sum_{i=1}^{n}\sum_{j=1}^{m}{\sum_{k=1}^{K}{v^k_i}W_{ij}h_j}+\sum_{i=1}^M{logZ_i}$$
  其中， $Z_i=\sum^k_{l=1}{exp(b_i^l+\sum_j{h_jWw_{ij}})}$
  对应的似然函数：
  $$p(v|\theta) = -\frac{1}{Z(\theta)}\sum_h{e^{-{E(v,h|\theta)}}}$$
  有了以上的定义，可以获得隐层和可见层的分布：
  $$p(v_i^k=1|h,\theta) = \frac{exp(a_i^k+\sum_j{h_j W_{ij}^k})}{\sum_{l=1}^Kexp(a_i^l+\sum_j{h_j W_{ij}^l})}$$
  $$p(h_j=1|v,\theta) = \sigma(b_j+\sum_{i=1}^m{\sum_{k=1}^K{v_i W_{ij}^k})}$$

  Conditional RBM’s

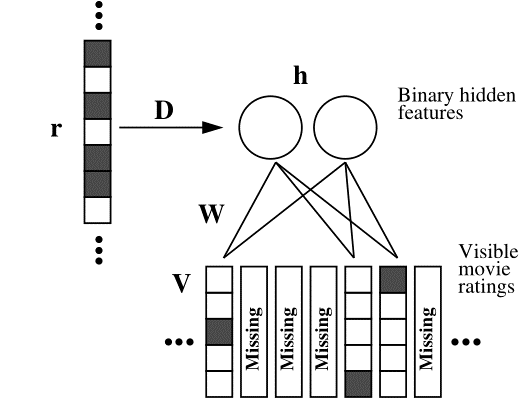
  其实在NetFlix的数据中，用户对电影的评分是比较稀疏。有大量的用户观看了电影没有评分，因此作者为了将此类信息加入到模型中，增加模型对用户评分的准确性。如图，将用户的观看列表信息加入到隐层中。
  
  原先每个隐层的分布变为：
  

  $$p(h_j=1|v,\theta) = \sigma(b_j+\sum_{i=1}^m{\sum_{k=1}^K{v_i W_{ij}^k})+\sum_{i=1}^M{r_iD_{ij}}}$$
  由于参数D与可见层无关，可以作为和b偏置一样的功能，参数更新也一样。

  NADE

  NADE是Hugo Larochelle在2011年提出，论文The Neural Autoregressive Distribution Estimator。具体引入NADE的原因还不是特别懂，看论文
  We describe a new approach for modeling the distribution of high-dimensional vectors of discrete variables. This model is inspired by the restricted Boltzmann machine (RBM), which has been shown to be a powerful model of such distributions. However, an RBM typically does not provide a tractable distribution estimator, since evaluating the probability it assigns to some given observation requires the computation of the so-called partition function, which itself is intractable for RBMs of even moderate size.

  可见层分布

  将RBM贝叶斯网络化，v为可见层节点，$v_{parent(i)}$可以理解为$v_i$的网络中的隐层节点。那么可见层的分布为：
  

  $$p(v)=\prod^D_i{p(v_i|v_{parents(i)})}$$
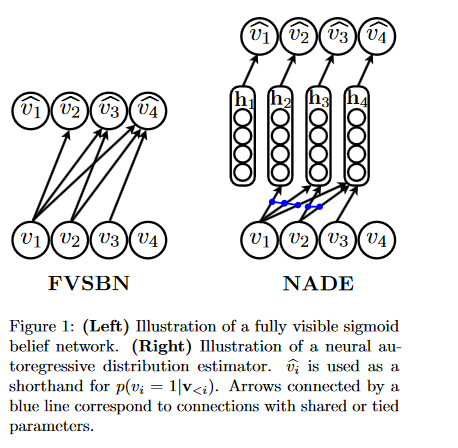
  现在有两种表征 $p(v_i|v_{parents(i)})$的方式，分别为FVSBM和NADE.
  

  FVSBM

  $$p(v_i|v_{parents(i)})=sigm(b_i+\sum_{j<i}{W_{ij}v_j})$$

  NADE

  $$p(v_i=1|v_{<i})=sigm(b_i+{(W^T)_{i}.h_i})$$
  $$h_i=sigm(c+{W,_{<i}v_{<i}})$$
  以上是NADE的可见层的分布公式，下面是求解流程：
  • #计算p(v)
  • a=c
  • p(v)=0
  • For i=1,2,…,D:
    
    • $h_i=sigm(a)$
    • $p(v_i=1|v_{<i})=simg(b_i+V_i.h_i)$
    • $p(v)=p(v)(p(v_i=1|v_{<i})^{v_i} + (1-p(v_i=1|v_{<i})^{1-v_i}))$
    • $a=a+W.,_iv_i$

  - EndFor

  • 计算梯度-log(p(v))
  • ${\delta{a}}=0$
  • ${\delta{c}}=0$
  • For i,2,…,D:
    
    • ${\delta{b_i}}=p(v_i=1|v_{<i}) - v_i$
    • ${\delta{V_i}}=(p(v_i=1|v_{<i}) - v_i)h^T_i$
    • ${\delta{h_i}}=(p(v_i=1|v_{<i}) - v_i)V^T_i$
    • ${\delta{c}}=\delta{c}+(\delta{h_i})h_i(1-h_i)$
    • $\delta{W,_i} = (\delta{a})v_i$
    • ${\delta{a}}=\delta{a}+(\delta{h_i})h_i(1-h_i)$
  • EndFor
  • 参数更新

  NADE-CF

  在以上铺垫后，就是讲应用加入到模型就行了。先定义一些参数$r^u={r^u_{m_{o1}},r^u_{m_{o2}},..,r^u_{m_{oD}}}$ 为用户的评分序列，$r^u_{m_{oi}}$为用户的评分，在1-k之间。
  

  $$p(r)=\prod^D_{i=1}{p(r_{m_{oi}} | r_{m_{o<i}})}$$
  $$h(r_{m_{o<i}})=g(c+\sum_{j<i}W^{r_{m_{oj}}}_{m_{oj}})$$
  另外，若写成每个用户对每个电影在评分K上的分布：
  $$p(r_{m_{oi}}=k|r_{m_{o<i}}) = \frac{exp(s^k_{m_{oi}}(r_{m_{o<i}}))}{\sum^K_q{exp(s^q_{m_{oi}}(r_{m_{o<i}}))}}$$
  $$s^k_{m_{oi}}(r_{m_{o<i}}) = b^k_{m_{oi}} + V^k_{m_{oi}}h(r_{m_{o<i}})$$

  目标函数

  $$-logp(r) = -\sum^D_i{logp(r_{m_{oi}}|r_{m_{o<i}}})$$

  参数共享

  $$h(r_{m_{o<i}})=g(c+\sum_{j<i}{\sum^{r_{m_{oj}}}_kW^{k}_{m_{oj}}})$$
  $$s^k_{m_{oi}}(r_{m_{o<i}}) = \sum_{j<k}{b^k_{m_{oi}} + V^k_{m_{oi}}h(r_{m_{o<i}})}$$