MATLAB数值法与微积分

最新推荐文章于 2022-06-28 21:54:13 发布

ytffhew

最新推荐文章于 2022-06-28 21:54:13 发布

阅读量1.1k

点赞数

本文链接：https://blog.csdn.net/ytffhew/article/details/83987476

版权

这篇博客介绍了MATLAB在数值方法和微积分中的应用，涵盖了差分函数、数值梯度、Laplacian、多項式微分和一阶微分方程的解法。文章通过实例展示了如ode45等求解器的使用，并探讨了刚性和非刚性问题。此外，还讨论了矩阵解法和非线性方程的解。

摘要由CSDN通过智能技术生成

分享一下我老师大神的人工智能教程！零基础，通俗易懂！http://blog.csdn.net/jiangjunshow

也欢迎大家转载本篇文章。分享知识，造福人民，实现我们中华民族伟大复兴！

第十二章數值法與微積分

12.1 前言

函數之微分為求函數對自變數之導數，或為其斜率；利用數值方法則可以解出其他相關之問題，其應用部份已在前章討論。數值微分有兩種應用，其一是在資料收集完備後，分析其變化速度；其二為即時估計或量測速率。後者需要快速演算法才能有立即反應。

計算斜率，依其定義即為dy/dx，在數值分析上必須轉化為可量測之變化量，亦即lim(Δy/Δx)。量取Δy或Δx則必須借助前後之數值點，例如Δx=x2-x1=x3-x2等關係。但這樣總是會因Δx值之大小而有差異。此時之Δx值也不可能如理論之無限小值。在實際之計算上，取Δx之前、後或中就有向前差分、向後差分或中心差分之區別。

12.2 差分函數diff

對於一個向量，差分函數在於求取該數列元素間之差異及其導數，相關指令格式如下：


Y = diff(X)
Y = diff(X,n)
Y = diff(X,n,dim)

若Ｘ為向量，則上述指令在於計算其相鄰元素間之差，亦即：


[X(2)-X(1)  X(3)-X(2) ... X(n)-X(n-1)]

若Ｘ為矩陣，則結果將計算其相鄰列間之差，如：


 [X(2:n,:) - X(1:n-1,:)].

參數n為階數，n=1時，其結果與Y = diff(X)相同，n=2時，其結果為diff(diff(X))，依此類推。因此每相差1其項數將減少一項。參數dim則是控制行向或列向差分，dim=1行向（預設值），dim=2為列向。

例：


>> x = 2:2:10
x =
  2     4     6     8    10

>> y=diff(x)
y =

  2     2     2     2

>> y=diff(x,2)
y =

  0     0     0

若間矩較細，將過差分後，其結果應為原函數之導數。


h = .01;
x = 0:h:pi;
d=diff(sin(x.^2))/h;
plot(x,sin(x.^2),x,[0 d],'r:')

上例等於計算sin(x.^2)之導數 2*cos(x.^2).*x，注意d值之長度會比x少１。

例：


>>X=(1:10).^2,

X =
1     4     9    16    25    36    49    64    81   100　

　>>x1=diff(X),x2=diff(X,2), x3=diff(y)

x1 =
3     5     7     9    11    13    15    17    19
x2 =
2     2     2     2     2     2     2     2
x3 =
2     2     2     2     2     2     2     2

結果為x1比Ｘ少一項，x2比x1又少一項，x2與x3相同，證明y3=diff(diff(X))。
例：


 X = [3 7 5 3;  2 0 8 4]
 x1=diff(X,1), x2= diff(X,1,2)

X =
3     7     5     3
2     0     8     4
x1 =
-1    -7     3     1
x2 =
4    -2    -2
-2     8    -4

例：正弦函數sin(t)以常態分布繪出[0 pi]間之區線及其第二導數cos(t)。


t=[0:pi/50:pi];nn=length(t);td=cos(t);
y=sin(t)+0.05*(randn(1,nn)-0.5);
dt1=diff(y)./diff(t);%backward(+)
dt2=(y(3:nn)-y(1:nn-2))./(t(3:nn)-t(1:nn-2));
plot(t,sin(t));hold on;plot(t,y,'b.');
plot(t,cos(t),'r:');
plot(t(1:nn-1),dt1,'k+');
plot(t(1:nn-2),dt2,'bo');

'+':向後差分；'o'中央差分

由其結果比較，中央差分比向後差分之誤差為小。可由其與實際值之相關係數可以確定。就向後差分者，相關係數為0.4927；而中央差分則為0.7674。


[r1,p1]=corrcoef(t(1:nn-1),dt1)
[r2,p2]=corrcoef(t(1:nn-2),dt2)

r1 =
1.0000   -0.4927
-0.4927    1.0000
p1 =
1.0000    0.0003
0.0003    1.0000
r2 =
1.0000   -0.7674
-0.7674    1.0000
p2 =
1.0000    0.0000
0.0000    1.0000

由於diff之前減特質，所以其功能亦可用來決定某些向量之特性，例如屬增加序列或減少序列，或所謂之單向(monotonic)系列，或屬等距分佈之系列等。下面的例子可作為一般之應用：

diff(x)==0　測試重複性之元素
all(diff(x)>0)　測試其單向性
all(diff(diff(x))==0)　測試各元素是否等距分佈

12.3 數值梯度gradient

12.3數值梯度gradient

一具有二自變數之函數F(x,y,z)，其梯度之定義為：


 ▽F = (dF/dx)i +(dF/dy)j +(dF/dz)k

其計算之指令格式如下：


 FX = gradient(F)
 [FX,FY] = gradient(F)
 [Fx,Fy,Fz,...] = gradient(F)
 [...] = gradient(F,h)
 [...] = gradient(F,h1,h2,...)

其中Ｆ為函數向量，切分後之間隔預設值為1，亦即h=1；若函數之變數增多，則h之值可因變數之不同另外設值。例如，h1可能屬於第一變數之區間；h2為第二變數之區間，而左邊之輸出值則依x,y,z之分量。

例一：


 v=-2:0.2:2;
 [x,y]=meshgrid(v);
 z=x.*exp(-x.^2-y.^2);
 [px,py]=gradient(z,.2,.2);
 contour(z),hold on, quiver(px,py), hold off

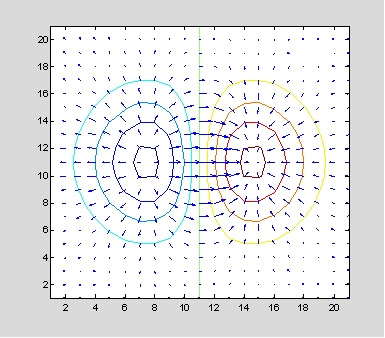
例二:

設有一向量Ｆ由魔術矩陣及巴斯上矩陣組成，其內容為：


>> F(:,:,1) = magic(3); F(:,:,2) = pascal(3);
>> F

F(:,:,1) =

     8     1     6
     3     5     7
     4     9     2


F(:,:,2) =

     1     1     1
     1     2     3
     1     3     6

取其梯度值，即▽F，設dx=1，dy=1，dz=1。則


>> gradient(F)

ans(:,:,1) =

    -7    -1     5
     2     2     2
     5    -1    -7


ans(:,:,2) =

         0         0         0
    1.0000    1.0000    1.0000
    2.0000    2.5000    3.0000

若間矩不同，即設dx=0.1，dy=0.1，dz=0.1。則▽F為



>> [PX,PY,PZ] = gradient(F,0.1,0.2,0.3) 

PX(:,:,1) =

  -70.0000  -10.0000   50.0000
   20.0000   20.0000   20.0000
   50.0000  -10.0000  -70.0000


PX(:,:,2) =

         0         0         0
   10.0000   10.0000   10.0000
   20.0000   25.0000   30.0000


PY(:,:,1) =

  -25.0000   20.0000    5.0000
  -10.0000   20.0000  -10.0000
    5.0000   20.0000  -25.0000


PY(:,:,2) =

         0    5.0000   10.0000
         0    5.0000   12.5000
         0    5.0000   15.0000


PZ(:,:,1) =

  -23.3333         0  -16.6667
   -6.6667  -10.0000  -13.3333
  -10.0000  -20.0000   13.3333


PZ(:,:,2) =

  -23.3333         0  -16.6667
   -6.6667  -10.0000  -13.3333
  -10.0000  -20.0000   13.3333

12.4 Del2--Laplacian

Del2指令--非連續Laplacian

若Ｕ矩陣為一個函數u(x,y)，其計算值係以該點之方格網絡為基準，則4*del2(U)是拉普拉斯運算函數Ｕ之估計值，是以固定差分法估算的方式。亦即令：


    L=▽²u/4 = (1/4)[d²u/dx² +d²u/dy²]

其中，


    L(ij)= (1/4)[u_i+1,j + u_i-1,j +u_i,j+u_i,i+1+u_i,j-1-u_i-1,j-1

上述L矩陣與U同大小，其值為四個相鄰點平均值。上式若為三度空間，則除數４要改為６。計算上述函數之指令格式如下：


　L = del2(U)
　L = del2(U,h)
　L = del2(U,hx,hy)
　L = del2(U,hx,hy,hz,...)

其中Ｕ矩陣之每點之間隔為1，亦即h=1，若h之值不同於1，則另設其值。若Ｕ為兩維函數，則其在Ｘ與Ｙ方向之間隔可用hx與hy另定，甚至三度空間也可加hz定義。

例：設U=x²+3y²，求其Laplacian向量



  [x, y]=meshgrid(-4:4,-3:3);
  U=x.*x+2*y.^2
  V=4*del2(U)

U =
 34    27    22    19    18    19    22    27    34
 24    17    12     9     8     9    12    17    24
 18    11     6     3     2     3     6    11    18
 16     9     4     1     0     1     4     9    16
 18    11     6     3     2     3     6    11    18
 24    17    12     9     8     9    12    17    24
 34    27    22    19    18    19    22    27    34
V =
  6     6     6     6     6     6     6     6     6
  6     6     6     6     6     6     6     6     6
  6     6     6     6     6     6     6     6     6
  6     6     6     6     6     6     6     6     6
  6     6     6     6     6     6     6     6     6
  6     6     6     6     6     6     6     6     6
  6     6     6     6     6     6     6     6     6