《机器学习》(周志华)第一章课后习题参考答案
1.1 求版本空间
题目:表1.1中若只包含编号为1和4的两个样例,试给出相应的版本空间。
P5:与训练集一致的“假设集合”我们称之为版本空间。本题即在假设空间中搜索包含正例且不包含反例的所有假设。(详细说明见后思考)
首先,用一个六位二进制数将整个假设空间表示出来,每两位描述一个属性。前两位取01表示色泽的取值为“青绿”,10表示色泽取值为“乌黑”,11表示色泽取值为 *。后四位分别表示根蒂与敲声的取值,以此类推.注意题中只包含1和4两个样例,因此假设空间中色泽的取值范围为:* ,乌黑、青绿;根蒂的取值范围为:*,蜷缩、稍蜷;敲声的取值范围为:*,浊响、沉闷。
假设空间
| 序号 | 色泽 | 根蒂 | 敲声 | 二进制表示 |
|---|---|---|---|---|
| 1 | * | * | * | 111111 |
| 2 | * | * | 浊响 | 111101 |
| 3 | * | * | 沉闷 | 111110 |
| 4 | * | 蜷缩 | * | 110111 |
| 5 | * | 稍蜷 | * | 111011 |
| 6 | 青绿 | * | * | 011111 |
| 7 | 乌黑 | * | * | 101111 |
| 8 | * | 蜷缩 | 浊响 | 110101 |
| 9 | * | 蜷缩 | 沉闷 | 110110 |
| 10 | * | 稍蜷 | 浊响 | 111001 |
| 11 | * | 稍蜷 | 沉闷 | 111010 |
| 12 | 青绿 | * | 浊响 | 011101 |
| 13 | 青绿 | * | 沉闷 | 011110 |
| 14 | 乌黑 | * | 浊响 | 101101 |
| 15 | 乌黑 | * | 沉闷 | 101110 |
| 16 | 青绿 | 蜷缩 | * | 010111 |
| 17 | 青绿 | 稍蜷 | * | 011011 |
| 18 | 乌黑 | 蜷缩 | * | 100111 |
| 19 | 乌黑 | 稍蜷 | * | 101011 |
| 20 | 青绿 | 蜷缩 | 浊响 | 010101 |
| 21 | 青绿 | 蜷缩 | 沉闷 | 010110 |
| 22 | 青绿 | 稍蜷 | 浊响 | 011001 |
| 23 | 青绿 | 稍蜷 | 沉闷 | 011010 |
| 24 | 乌黑 | 蜷缩 | 浊响 | 100101 |
| 25 | 乌黑 | 蜷缩 | 沉闷 | 100110 |
| 26 | 乌黑 | 稍蜷 | 浊响 | 101001 |
| 27 | 乌黑 | 稍蜷 | 沉闷 | 101010 |
若两个假设的二进制表示分别为A和B,则 A | B==A ⇒ B⊂A,A&B==B ⇒ B⊂A.(任意一个等式都可以判断出假设A是否包含假设B)
设P为假设1(正例),N为假设4(反例),假设H只要满足H | P==H && H | N != H为真,那么假设H就应该被包含在版本空间内。遍历假设空间内的所有假设进行上述判断,就可以获得版本空间内的所有假设。
#include<stdio.h>
int hypo_const[27] = {0x3f,0x3d,0x3e,0x37,0x3b,0x1f,0x2f,0x35,0x36,0x39,0x3a,0x1d,0x1e,0x2d,0x2e,
0x17,0x1b,0x27,0x2b,0x15,0x16,0x19,0x1a,0x25,0x26,0x29,0x2a};
void main()
{
int sample[2] = {0x15,0x2a},sum=0;
for(int i=0;i<27;i++)
{
if( (hypo_const[i] | sample[1] ) != hypo_const[i] && (hypo_const[i] | sample[0]) == hypo_const[i] )
{
sum++;
printf("%x %d\n",hypo_const[i],i+1);
}
}
printf("\nsum:%d\n\n",sum);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
求得版本空间为假设2、4、6、8、12、16、20.
版本空间
| 序号 | 色泽 | 根蒂 | 敲声 | 二进制表示 |
|---|---|---|---|---|
| 2 | * | * | 浊响 | 111101 |
| 4 | * | 蜷缩 | * | 110111 |
| 6 | 青绿 | * | * | 011111 |
| 8 | * | 蜷缩 | 浊响 | 110101 |
| 12 | 青绿 | * | 浊响 | 011101 |
| 16 | 青绿 | 蜷缩 | * | 010111 |
| 20 | 青绿 | 蜷缩 | 浊响 | 010101 |
思考:书中P5提到,版本空间的求法为遍历假设空间,不断删除与正例不一致的假设和(或)与反例一致的假设。按照我的理解,版本空间有以下3种不同的求法。
- 删除不能包含所有正例以及包含任意反例的假设
- 删除不能包含所有正例的假设
- 删除包含任意反例的假设
-
本题使用了第一种方法来求版本空间,三种求法的选择应该属于归纳偏好的范畴。
1.2 求假设空间大小
题目:与使用单个合取式来进行假设表示相比,使用“析合范式”将使得假设空间具有更强的表示能力。若使用最多包含k个合取式的析合范式来表达表1.1西瓜分类问题的假设空间,试估算有多少种可能的假设。
分析:本题可以延续上一题的假设表述方法,每个合取式用一个8位二进制整数来表示,则一共有48个数待选。遍历C(48,k)种可能的选取组合,求出每种组合中k个合取式的合并结果,再去掉重复和冗余的情况,就是包含k个合取式的析合范式所能表达的假设空间大小。请注意,题目所述为“最多包含k个合取式的析合范式”,也就是说1,2,3…k个合取式组成的析合范式都满足条件,而不是仅考虑k个合取式组成的析合范式。
难点:
1. 假设空间太大,穷举所有组合不现实。
2. 合取式的合并结果(析取式)如何求,如何用一个整数表示。先来看难点2
前文所述的表示方法,合取式的合并算法十分低效,因此有必要定义一种新的表达方式。在48个基本假设(基本合取式)中,有2*3*3=18个叶子假设(叶子合取式):每个特征的取值都为具体值。任何合取式、析取式都可以用这18个叶子合取式的组合来表示。因此可以用一个18位的二进制整数来表示任意假设:将18个叶子合取式编号,若某假设包含序号为1的叶子合取式,则该假设第一位为1,否则第一位为0。其它位类推。在这种新的表达方式下,合并合取式(或析取式)A,B,只需作 C=A|B 的按位或运算,C即为表示A、B合并析取式的整数。(C语言按位或运算的速度非常快)
新的表达方式下,代表每个假设整数的求法如下:
1.将48个基本合取式的旧表达式存在数组hypo_old中
2.将18个叶子合取式的旧表达式存在数组hypo_leaf中
3.对hypo_old中的每个元素,循环对hypo_leaf中的18个元素xi作如下判断:若A|xi==A,则Anew中第i位为1,否则Anew中第i为为0.
将新的表达结果(48个整数)存在hypo_const中。
这种表达方式不仅大大提高了合并合取式算法的效率,还让我们有了一个额外发现:本题的最大假设空间大小为262143.为什么会有这个结论呢?原因就是18位二进制整数所能表示的最大范围即262143,又因为析取范式不考虑空集∅,即整数不为0,因此假设空间的大小即262143.这个结论非常重要,甚至一定程度上它就是本道题的答案(k足够大)。难点1
如图所示,以k=3时为例,遍历C(48,3)中所有组合的情况实际上就是3个标记依次不断向右移动的过程。序号大的标记,总是在序号小的标记的右侧。

在移动过程中,我们总是先确定标记1的位置(初始记为1),然后在标记1的右侧确定标记2的位置(初始记为1+1)……直到确定标记k的位置(初始记为k-1+1,这么写有些奇怪,原因下面会讲)。每确定完一次标记k,就形成一次组合。之后,将标记k自增,若标记k≤48,则又形成新的组合,继续自增;若标记k>48,则标记k越界,转而向前先寻找标记k-1的位置(自增),若k-1也越界(标记k-1>47),继续向前寻找标记k-2位置(自增),直到向前寻得标记k-i自增后不越界(标记k-i≤48-i),此时调转趋势,向后寻找标记k-i+1的位置(递增,值为标记k-i的值+1),直到标记k的位置(标记k-1的值+1)。
确定方式:每个标记有两种可能的确定方式。若是从后面的标记越界返回,则改变方式为自增,若是从前面的标记顺序向下确定,则改变方式为递增(上一个标记的值+1)。额外规定:1.形成一次组合后,标记k的改变方式为自增。2.标记1的改变方式总为自增。
优化方法:
动态申请长度为k的一维数组poslist和hypo_process,poslist用来保存k个标记的位置,hypo_process用来保存前k个合取式合并的结果。用整数posflag来记录当前需要确定的标记序号。
每次确定完标记poslist[posflag]后(自增并通过越界判断),则将前posflag个合取式的合并结果存进hypo_process[posflag],即hypo_process[posflag]=hypo_process[posflag-1]|hypo_const[poslist[posflag]]若hypo_process[posflag]==hypo_process[posflag-1] || hypo_process[posflag]==0x3ffff&&posflag<k说明出现冗余,当前标记自增,即poslist[posflag]++,先进行越界判断,再进行上述判断。都通过后,posflag++,进而确定下一个标记的位置(递增),直到posflag==k,形成一个组合,将hypo_process[k]验重后计数。
注意:计数前应该判断是否重复。
因为不同的析取范式,有可能表示同一种假设。比如:(色泽=*,根蒂=*,敲声=浊响)∨(色泽=*,根蒂=*,敲声=清脆)∨(色泽=*,根蒂=*,敲声=沉闷)与(色泽=乌黑,根蒂=*,敲声=*)∨(色泽=青绿,根蒂=*,敲声=*)是同一种假设,它们都表示(色泽=*,根蒂=*,敲声=*),它们在18位整数的表示方法下,对应的整数是唯一的。因此,只有原先未出现此数(此假设),才能将其记录并且计数值自增。否则重复,不计数。由于难点1中我们发现假设空间大小为262143,因此申请一个大小为262143的数组hypo_appear来记录每个假设出现与否。出现则数组对应元素记为1,未出现为0。(如果没有求出这个数,则每个数字出现与否只能用一个队列来记录,判断重复的算法效率非常底下,这就是此数的重要性)最后,分析中已经提到,题目中要求的是“最多包含k个合取式的析合范式”,因此在for循环中让k从1变到18,执行18次count,在k增加时,hypo_appear中的内容不清空,且计数n_count不归零,就能包含1,2……k个合取式的情况。
代码如下,运行时间在5秒左右:#include<stdio.h> int hypo_old[48] = {0xff,0xf9,0xfa,0xfc,0xcf,0xd7,0xe7,0x7f, 0xbf,0xc9,0xca,0xcc,0xd1,0xd2,0xd4,0xe1, 0xe2,0xe4,0x79,0x7a,0x7c,0xb9,0xba,0xbc, 0x4f,0x57,0x67,0x8f,0x97,0xa7,0x49,0x4a, 0x4c,0x51,0x52,0x54,0x61,0x62,0x64,0x89, 0x8a,0x8c,0x91,0x92,0x94,0xa1,0xa2,0xa4}; int hypo_leaf[18] = {0x49,0x4a, 0x4c,0x51,0x52,0x54,0x61,0x62,0x64,0x89, 0x8a,0x8c,0x91,0x92,0x94,0xa1,0xa2,0xa4}; int hypo_const[48]= {0}; int new_leaf[18] = {0x20000,0x10000, 0x08000,0x04000,0x02000,0x01000, 0x00800,0x00400,0x00200,0x00100, 0x00080,0x00040,0x00020,0x00010, 0x00008,0x00004,0x00002,0x00001}; int count(int n_n,int n_k,int &n_count,int *hypo_appear) { // n_count=0; int i; // for(i=0;i<262143;i++) // hypo_appear[i] = 0; int *poslist,*hypo_process,posflag,trend; poslist = new int[n_k]; hypo_process = new int[n_k]; for(i=0;i<n_k;i++) { poslist[i] = -1; } posflag = 0; while(1)//poslist[0] <= n_n-n_k { if(posflag == 0) //如果是第一个则自增,如果超出则退出,否则直接赋值,赋值后如未达个数提前到0x3ffff跳过该点,否则进入下一轮 { poslist[posflag]++; if(poslist[0] > n_n-n_k) break;//*****整个循环的退出口*****// hypo_process[posflag] = hypo_const[poslist[posflag]]; //直接赋值 if(hypo_process[posflag] == 0x3ffff && posflag<n_k-1)//提前到0x3ffff跳过 continue; else { posflag++; trend = 1;//上升趋势 } } else //上升趋势递增,下降趋势自增,如果超出则位数下降回滚上一轮,否则加入本轮假设,若无变化则跳过该点,如果未达个数提前到0x3ffff也跳过该点,否则进入下一轮 { if(trend == 1) poslist[posflag] = poslist[posflag-1] + 1; else poslist[posflag]++; if(poslist[posflag] > n_n-n_k+posflag)//超出则位数下降 { posflag--; trend = 0; continue; } hypo_process[posflag] = hypo_process[posflag-1] | hypo_const[poslist[posflag]];//加入本轮假设 if(hypo_process[posflag] == hypo_process[posflag-1] || hypo_process[posflag] == 0x3ffff && posflag<n_k-1) //跳过部分 { trend = 0;//跳过等同回滚,自增 continue; } posflag++; trend = 1; } if(posflag == n_k)//说明k个析合范式已经全部形成 { posflag--; trend = 0; if(hypo_appear[hypo_process[posflag]-1]==0) { n_count++; hypo_appear[hypo_process[posflag]-1] = 1; } //错误写法:n_count++; /* 应该判断是否重复。 不同的析取范式,有可能表示同一种假设。 比如:(色泽=*,根蒂=*,敲声=浊响)∨(色泽=*,根蒂=*,敲声=清脆)∨(色泽=*,根蒂=*,敲声=沉闷) 与(色泽=乌黑,根蒂=*,敲声=*)∨(色泽=青绿,根蒂=*,敲声=*)是同一种假设, 它们都表示(色泽=*,根蒂=*,敲声=*),它们在18位整数的表示方法下,对应的整数是唯一的。 因此,只有在原先未出现此数(此假设)的情况下,才能将计数值自增。否则重复,不计数。 */ } } delete poslist; delete hypo_process; return n_count; } void main() { for(int i=0;i<48;i++)//难点2,形成新表达式 { for(int j=0;j<18;j++) { if( (hypo_old[i] | hypo_leaf[j]) == hypo_old[i]) hypo_const[i] |= new_leaf[j]; } } int change = 0,temp; int n_count=0; int *hypo_appear = new int[262143]; for(i=0;i<262143;i++) hypo_appear[i] = 0; for(i=1;i<=18;i++) { count(48,i,n_count,hypo_appear); printf("length %-2d : %-10d\n",i,n_count); } } /* length 1 : 48 length 2 : 897 length 3 : 8385 length 4 : 41742 length 5 : 115821 length 6 : 201303 length 7 : 248853 length 8 : 260787 length 9 : 262143 length 10 : 262143 length 11 : 262143 length 12 : 262143 length 13 : 262143 length 14 : 262143 length 15 : 262143 length 16 : 262143 length 17 : 262143 length 18 : 262143 */- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
可以看到,使用最多包含9个合取式的析合范式,就可以表示整个假设空间。
如果对“只包含 k个合取式的析合范式”这个问题感兴趣,那么将27,29,30行的注释去掉即可。答案如下:
length 1 : 48
length 2 : 865
length 3 : 8028
length 4 : 39861
length 5 : 109686
length 6 : 186102
length 7 : 216036
length 8 : 197362
length 9 : 155382
length 10 : 106762
length 11 : 63004
length 12 : 31180
length 13 : 12616
length 14 : 4048
length 15 : 988
length 16 : 172
length 17 : 19
length 18 : 1
可以看到表示能力最强的是只包含7个合取式的析合范式,但也不能表示出假设空间中所有的262143个假设。当k=18时,只能选取18个叶子合取式才不会产生冗余,因此只能表示(色泽=*,根蒂=*,敲声=*)这一种假设。k>18就没有意义了,因为必定会产生冗余。1.3 归纳偏好设计
题目:若数据包含噪声,则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下,设计一种归纳偏好用于假设选择。
分析:既然数据中包含噪声,最直接的思路就是首先去除噪声。去噪方法:若存在两个样例属性取值都相同,标记却不同,则只保留标记为正例的样例(或标记为反例的样例,也可以考虑更加复杂的筛选方法,比如统计相似样例的标记),在此基础上求出版本空间。
也可以考虑其他方法:
1.在求版本空间时,只除去与反例不一致的假设。
2.求版本空间时,只留下包含了所有正例的假设。1.4 “没有免费的午餐定理”拓展证明
题目:本章1.4节在论述“没有免费的午餐”定理时,默认使用了“分类错误率”作为性能度量来对分类器进行评估。若换用其他性能度量l,则式(1.1)将改为
试证明“没有免费的午餐定理”仍成立。
证明:
在证明定理之前,先构造一个引理:
引理1:在二分类问题下,对任意性能度量指标ll
证毕.
现在证明定理:
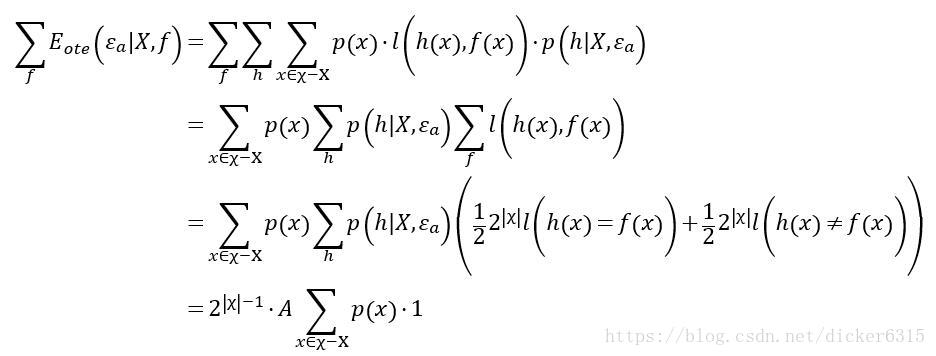
上式说明度量结果与学习算法εa无关,“没有免费的午餐定理”仍然成立。
证明完毕。
关于证明的补充说明:本文的引理没有考虑第二章2.3节中的代价敏感错误。若本题中考虑代价敏感错误,则各种不同代价错误出现的概率也是满足平均分布的,引理1仍然成立,但是证明过程会更加复杂。
思考: NFL定理证明过程中假设了f均匀分布,并且目标是学习所有的真实函数f。现实生活中,具体的学习算法无需学习所有的真实函数,因为所有真实函数在现实中的映射即天底下所有问题都可以用相同的这一组特征来描述,这是不现实的。若用同一组特征来描述所有问题,那么分类结果必将杂乱无章没有任何规律可言,这也是书中假设f满足均匀分布的原因。真实情况下,也许没有任何一种分布能够描述其特征。因此NFL并不意味着好的学习算法没有意义。1.5 试述机器学习能在互联网搜索的哪些环节起作用
1.在向搜索引擎提交信息的阶段,能够从提交文本中进行信息提取,进行语义分析。
2.在搜索引擎进行信息匹配的阶段,能够提高问题与各个信息的匹配程度。
3.在向用户展示搜索结果的阶段,能够根据用户对结果感兴趣的程度进行排序。























 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








