算法总结-最短距离和问题

第一种：纯种最短距离和

形式1：在坐标轴上有一些点，你可以在其中任意一点放置某种东西，求放置点到所有点的最小和

形式2：将所有值改成相等的某个值，每次修改可以进行加1或者减1，求最少操作数

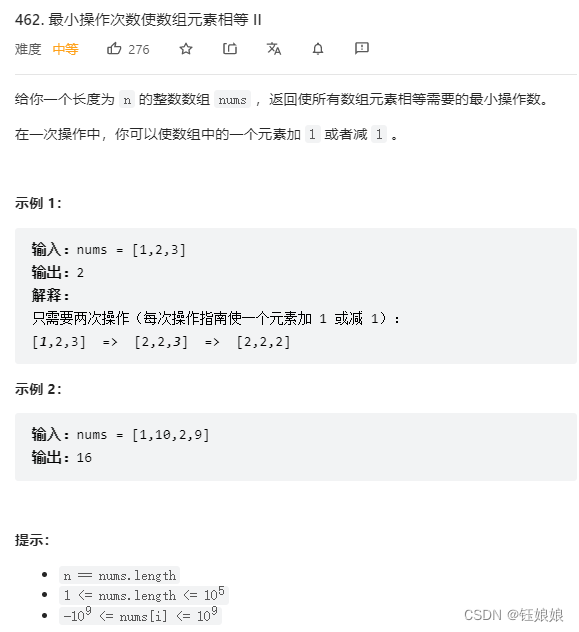
上图源自力扣462

这种距离总和问题的统一解法，是吧这个 相等值/坐标位置 放置在中间数上。

 为什么放中间数距离和最小呢？

假设四个点，放在最左侧，第一段线段计算3次，第二段计算2次，第三段计算1次

放中间的话：

则两侧计数都会减少 

四个数的情况，放左右两侧效果相同，中间一段都算了两次，也就是偶数放在中间任意位置的一个可以使得距离和最小

奇数情况，放中间即可，上下两部分距离是相等的，因此也可以双指针计算差值的和 

class Solution {
    public int minMoves2(int[] nums) {
        Arrays.sort(nums);
        int ans = 0;
        int n = nums.length;
        for(int i = 0,j=n-1; i < j; i++,j--){
            ans += nums[j]-nums[i];
        }
        return ans;
    }
}

第二种：加权最短距离和

力扣-2448

有权值的情况，我们可以按数值变化修改两侧水位线求解。

1. 假设都降到最低值，我们可以计算出一个开销 rightSum，右侧开销总和rightCostSum=XX,以及rightLen=n,左侧开销leftSum=0，以及左侧长度leftLen=0,leftCostSum=0

2. 那么此时我们往右移会发生什么呢？

        左侧长度为 leftLen 个元素，每个增加了 v[i]-v[i-1]，每一份的开销都会消耗 leftCostSum 的总开销（rightSum为对应方向所有cost之和），总计增加消耗 (v[i]-v[i-1])*(leftCostSum)

        右侧长度为 rightLen 个元素，每个减少了 v[i]-v[i-1]，每一份的开销都会减少 rightCostSum,总计减少消耗 (v[i]-v[i-1])*(rightCostSum)

3. 通过这个移动水位线的方式，我们可以计算完成所有位置的消耗

class Solution {
        public long minCost(int[] nums, int[] cost) {
            int n = nums.length;
            Integer[] sort = new Integer[n];
            for(int i = 0; i < n; i++) sort[i] = i;
            Arrays.sort(sort,(a,b)->nums[a]-nums[b]);
            int min = nums[sort[0]];
            int max = nums[sort[n-1]];

            long leftSum = 0;
            long rightSum = 0L;
            for(long c:cost) rightSum += c;
            long curr=0;
            for(int i = 0; i < n; i++){
                curr += ((long)nums[i]-min)*(long)cost[i];
            }
            long ans = curr;
            for(int i = min+1,j=0; i <= max; i++){
                while (j<n&&nums[sort[j]]<i){
                    leftSum+=cost[sort[j]];
                    rightSum-=cost[sort[j]];
                    ++j;
                }
                curr = curr-rightSum+leftSum;
                ans = Math.min(ans,curr);
            }
            return ans;
        }


    }

 第三种：步长变换

 

力扣-2033

这题不一样的地方是多了一个步长，其实这个二维没有意义，当成一维去解就可以了，不同的是，步长会多了一个判断能否成功，比如步长是2，一个1一个2必然无法相等，所以这题需要增加一个同余的判断，其他与第一题相同

第四种，割补法

 力扣-1684

1. 需要把1的位置转换为实际距离0点的距离，然后求得值就比较接近最小距离和了，我们先 把它当成最小距离和去求，那么完全可以采用类似第二种的处理方式，得到最小距离和

2. 偏差，左右两侧可以使用左割右补的方式，把同一位置改为相邻位置

1. 简化问题。假设我们不限制连续K个。

   • 那么实际上，本题可看做是1的位置距离坐标轴起点的各个值，中间放置一点加油站，形成距离和的最小值问题
   • 多点求最短距离和，最佳方式是放在中位数上
   • 因此我们可以先把本题换成1距离坐标轴起点的位置，也就是索引值

2. 限制长度K，就是长度 N 上，我们只需要其中 K 个节点的连续值。那么我们可以考虑 从 MID（MID是K/2） 到 N-MID2（MID2是K-K/2） 上面的所有值

3. 计算次数

   

   • 首先图中的长条代表面积，前缀和代表当前长条和上面所有长条的距离之和
   • 有前缀和就意味着可以计算任意一行到后面某一行的面积和
   • 假设以红色条4为核心，则我们需要的面积是 红色长条*左半边长度MID（MID是K/2）-（左半边前缀和差）-等差数列。为什么要减掉个等差数列呢？因为我们计算过程中，实际上是把左边所有元素平移到4的位置。实际是对于前一个元素，只需要移动到3，再前一个只需要移动到2，逐步递减，所以就形成了一个需要减掉的等差数列
   • 对于右侧元素，我们需要的面积是 右侧前缀和-红色长条*MID2-等差数列2，如黄色部分，是需要减掉的等差数列。
   • 最终在红色长条上下的蓝色部分，即为答案
   • 枚举所有中心节点获得最优解

class Solution {
        public int minMoves(int[] nums, int k) {
            int n = nums.length;
            int sum = 0;
            for(int num:nums) sum += num;
            long[] arr = new long[sum];
            for(int i =0,j=0;i<n;i++){
                if(nums[i]==1) arr[j++]=i;
            }
            for(int i =1;i<arr.length;i++){
                arr[i] = arr[i]+arr[i-1];
            }
            long ans = Long.MAX_VALUE;


            int half1 = (k+1)/2;
            int half2 = k-half1;
            for(int i = half1-1; i < arr.length-half2;i++){
                long iPre = (i-1<0?0:arr[i-1]);
                long halfPre = i-half1<0?0:arr[i-half1];
                long leftSum = (arr[i]-iPre)*(long)(half1)-(arr[i]-halfPre);
                long rightSum = arr[i+half2]-iPre-(arr[i]-iPre)*(half2+1);
                long leftCost = leftSum-((long)(half1)*(half1-1)/2);
                long rightCost = rightSum-((long)(half2)*(half2+1)/2);
                ans = Math.min(ans,leftCost+rightCost);
            }

            return (int) ans;
        }
    }

时间复杂度：O(N+M)，N为原数组长度，M为1的个数
空间复杂度：O(M)

 第五种，放置K个点最短距离和

通过第一种情况，我们知道，如果确定了范围，距离一个点的最短距离和，最佳放置方式是把它放中间。那么对于K个点的情况，我们只要枚举前一个部分的分割点即可。特别地，第一个的点的放置的起始位置只能是开头。

1. 假设一组房子拥有一个邮筒，则邮筒，应该尽可能地放在房子中间
   • 奇数放在中间
   • 偶数放在中间两个的任意一个位置
2. 于是想到动态规划，以某点为终点，消耗几个邮筒对应的最小距离
3. 枚举邮筒个数，以及前一个邮筒范围的结束位置，在上一个邮筒位置的基础上，把当前邮筒放在这段房子的中间，比较最小距离

class Solution {
    public int minDistance(int[] houses, int k) {
        Arrays.sort(houses);
        int n  =houses.length;
        int[][] dp = new int[n][k+1];
        for(int i = 0; i < n; i++){
            Arrays.fill(dp[i],Integer.MAX_VALUE/2);
            dp[i][0] = 0;
        }

        for(int i=0; i < n; i++){
            for(int j = 1; j <= Math.min(i+1,k); j++){
                for(int t = 0; t <= i;t++){
                    dp[i][j]=Math.min((t==0?0:dp[t-1][j-1])+getDis(houses,t,i),dp[i][j]);
                    if(j==1) break;
                }
            }
        }

        return dp[n-1][k];
    }

    private int getDis(int[] houses, int i, int j){
        int ans = 0;
        while(i<j){
            ans += houses[j--]-houses[i++];
        }
        return ans;
    }
}

时间复杂度：O(n^2*k+nlogn)
空间复杂度：O(nk)