【点云处理之论文狂读经典版10】—— PointCNN: Convolution On X-Transformed Points

摘要

• 问题： CNN之所以那么成功，那是因为convolution operator能够利用网格数据中的spatially-local correlation。但是点云是无规则且无序的，因此直接使用kernel对点特征进行卷积将会导致形状信息的丢失以及点云顺序的变化
• 方法： 提出了一个简单通用的框架PointCNN，用于点云的特征学习，从输入点中学习$\mathcal{X}$-transformation，在两个方面得到较好的效果：
  ①与这些点相关联的输入特征的权重
  ②将点的排序映射到一个潜在且canonical的顺序
  在$\mathcal{X}$-transformation特征空间上还会使用convolution operator的元素间乘法和加法操作
• 代码：
  ①https://github.com/yangyanli/PointCNN TensorFlow版本
  ②https://github.com/pyg-team/pytorch_geometric PyTorch版本，这是一个库，将PointCNN封装成了一个函数
  ③https://github.com/nicolas-chaulet/torch-points3d 集中复现了很多篇经典的文章

引言

假设$C$维输入特征的无序集合 F = { f a , f b , f c , f d } \mathbb{F}=\left\{ {{f_a},{f_b},{f_c},{f_d}} \right\} F={fa​,fb​,fc​,fd​}在图1(($i$)-($iv$))中所有的情况下都是相同的，并且有大小为$4\times C$的kernel $\mathbf{K}={\left[k_{\alpha },k_{\beta },k_{\gamma },k_{\delta }\right]}^T$。

在图1($i$)中，遵循着给定规律网格的结构，局部$2\times 2$patch中的特征可以写成大小为$4\times C$的${\left[f_a,f_b,f_c,f_d\right]}^T$，通过与$\mathbf{K}$进行卷积，得到 $f_i=\mathrm{Conv}\left(\mathbf{K},{\left[f_a,f_b,f_c,f_d\right]}^T\right)$，其中$\mathrm{Conv}(\cdot ,\cdot )$是一个简单的元素间相乘并且进行sum${}^2$的操作。

在图1$(ii),(iii)$ 和 $(iv)$中，这些点的顺序是任意的。根据图中的顺序，输入特征集合$\mathbb{F}$在$(ii)$ 和 $(iii)$中可以写成${\left[f_a,f_b,f_c,f_d\right]}^T$，在$(iv)$中可以写成${\left[f_c,f_a,f_b,f_d\right]}^T$。基于此，如果直接使用convolution operator，三种情况的输出特征参见图1中的公式(1a)。我们可以注意到，在任何情况下$f_{ii}\equiv f_{iii}$都成立，而且在大多数情况下$f_{iii}\ne f_{iv}$成立。这个例子表明直接使用卷积会导致形状信息的缺失($f_{ii}\equiv f_{iii}$)和顺序的变化($f_{iii}\ne f_{iv}$)。

本文提出使用多层感知机学习$K\times K\mathcal{X}$-transformation，对$K$个输入点云$\left(p_1,p_2,\dots ,p_K\right)$的坐标进行变换，即$\mathcal{X}=MLP\left(p_1,p_2,\dots ,p_K\right)$。我们的目标是使用这个变换同时对输入的特征进行赋权和排序，随后对变换后的特征进行卷积。上述的步骤可以称为$\mathcal{X}$-Conv，是PointCNN中的一个基础block。$\mathcal{X}$-Conv在$(ii),(iii)$和 $(iv)$中可以表示成图1中公式(1b)，其中$\mathcal{X}$s是一个$4\times 4$的矩阵，因为图中$K=4$。我们可以注意到，因为${\mathcal{X}}_{ii}$和${\mathcal{X}}_{iii}$是从不同形状中学习得到的，所以它们可以有所不同，从而对输入特性施加相应的权重，并且达到$f_{ii}\ne f_{iii}$的效果。对于${\mathcal{X}}_{iii}$ 和 ${\mathcal{X}}_{iv}$，如果它们通过学习后能够满足${\mathcal{X}}_{iii}={\mathcal{X}}_{iv}\times \Pi$，其中$\Pi$是将$(c,a,b,d)$排序为$(a,b,c,d)$的排序矩阵的话，那么也可以达到$f_{iii}\equiv f_{iv}$的效果。

通过图1中的例子分析可以看出，在理想$\mathcal{X}$-transformation下，$\mathcal{X}$-Conv能够考虑到点的形状，同时具有排序不变性。事实上，我们发现学习到的$\mathcal{X}$-transformation与我们想的差远了，尤其是在排序不变性的方面。但是，基于$\mathcal{X}$-Conv的PointCNN的性能要比现有方法的性能都要好。

PointCNN

Hierarchical Convolution

在介绍PointCNN中的hierarchical convolution之前，先简要地介绍其在规则网格上的应用，如图2上所示。对于基于CNN的网格而言，输入是大小为$R_1\times R_1\times C_1$的特征图${\mathbf{F}}_1$，其中$R_1$是空间分辨率，$C_1$是特征通道数。大小为$K\times K\times C_1\times C_2$的kernel和${\mathbf{F}}_1$中大小为$K\times K\times C_1$的patches进行卷积，得到另外一个大小为$R_2\times R_2\times C_2$的特征图${\mathbf{F}}_2$。在图2上中，$R_1=4,K=2$, $R_2=3$。与特征${\mathbf{F}}_1$x相比，${\mathbf{F}}_2$的空间分辨率很低($\left(R_2<R_1\right)$)，但是具有更深的通道数($\left(C_2>C_1\right)$)，并且具有更高层的信息。

PointCNN的输入为 F 1 = { ( p 1 , i , f 1 , i ) : i = 1 , 2 , … , N 1 } \mathbb{F}_{1}=\left\{\left(p_{1, i}, f_{1, i}\right): i=1,2, \ldots, N_{1}\right\} F1​={(p1,i​,f1,i​):i=1,2,…,N1​}，其中 { p 1 , i : p 1 , i ∈ \left\{p_{1, i}: p_{1, i} \in\right. {p1,i​:p1,i​∈ ${\mathbb{R}}^{\text{Dim }}\}$是一组点，还有每个点对应的特征$\left\{f_{1,i}:f_{1,i}\in {\mathbb{R}}^{C_1}\right\}$。根据基于网格CNN的分层构造，在 ${\mathbb{F}}_1$上应用$\mathcal{X}$-Conv 便可得到更高层的表示${\mathbb{F}}_2=\left\{\left(p_{2,i},f_{2,i}\right):f_{2,i}\in {\mathbb{R}}^{C_2},i=1,2,\dots ,N_2\right\}$，其中 { p 2 , i } \left\{p_{2, i}\right\} {p2,i​}是 { p 1 , i } \left\{p_{1, i}\right\} {p1,i​}的一组表示点，${\mathbb{F}}_2$ 的的空间分辨率比${\mathbb{F}}_1$小，${\mathbb{F}}_2$的通道数比${\mathbb{F}}_1$多，即$N_2<N_1$, $C_2>C_1$。当上述操作循环进行后，带有输入点的特征会被“投影”或是“聚合”到更少的点，但是每个点的特征信息却是更加丰富。

{ p 2 , i } \left\{p_{2, i}\right\} {p2,i​}中的点在分类任务中是通过 { p 1 , i } \left\{p_{1, i}\right\} {p1,i​}随机下采样得到的，在分割任务中是通过Farthest Point Sampling(FPS)算法得到的，因为分割任务更需要均匀的点分布。如果有更好的方法选择点，那么最终的结果肯定会更好，在以后的工作中会进行深入的研究。

$\mathcal{X}$-Conv Operator

$\mathcal{X}$-Conv 在点云的局部区域中进行操作，由于输出特性应该与表示点 { p 2 , i } \left\{p_{2, i}\right\} {p2,i​}相关联，因此$\mathcal{X}$-Conv将它们在 { p 1 , i } \left\{p_{1, i}\right\} {p1,i​}中的邻域点、相关的特性作为输入，以进行卷积。为了更简单地描述，记$p$为 { p 2 , i } \left\{p_{2, i}\right\} {p2,i​}中的表示点，$p$的特征为 $f$，$p$在 { p 1 , i } \left\{p_{1, i}\right\} {p1,i​}的相邻点为$\mathbb{N}$。因此，对于特定点$p$而言，$\mathcal{X}$-Conv的输入为 S = { ( p i , f i ) : p i ∈ N } \mathbb{S}=\left\{\left(p_{i}, f_{i}\right): p_{i} \in \mathbb{N}\right\} S={(pi​,fi​):pi​∈N}。$\mathbb{S}$是一组无序的集合。在不失一般性的情况下，$\mathbb{S}$可以写成$K\times Dim$的矩阵$\mathbf{P}={\left(p_1,p_2,\dots ,p_K\right)}^T$和$K\times C_1$的矩阵$\mathbf{F}={\left(f_1,f_2,\dots ,f_K\right)}^T$，$\mathbf{K}$ 表示要训练的kernel。有了这些输入，就能计算$p$的输出特征：
$${\mathbf{F}}_p=\mathcal{X}-\mathrm{Conv}(\mathbf{K},p,\mathbf{P},\mathbf{F})=\mathrm{Conv}\left(\mathbf{K},\mathrm{MLP}(\mathbf{P}-p)\times \left[ML{P}_{\delta }(\mathbf{P}-p),\mathbf{F}\right]\right),$$
其中$ML{P}_{\delta }(\cdot )$是单独作用在一个点上的多层感知机，在$\mathcal{X}$-Conv 的所有操作，$\mathrm{Conv}(\cdot ,\cdot ),\mathrm{MLP}(\cdot )$, 矩阵乘法 $(\cdot )\times (\cdot )$和 $ML{P}_{\delta }(\cdot )$都是可导的，那么$\mathcal{X}$-Conv 也是可导的，因此可以被用到其他的反向传播神经网络中。

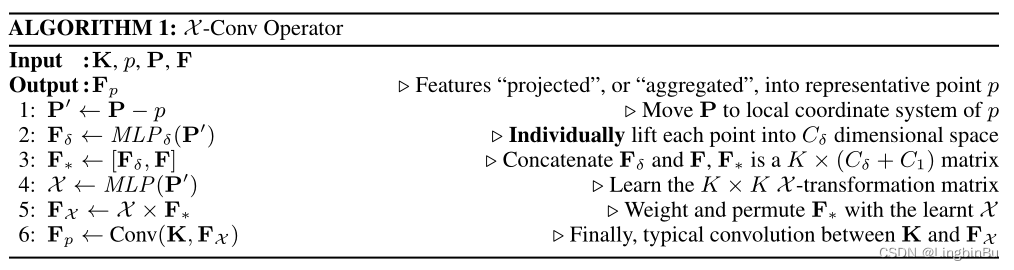
算法1中的第4-6行主要表述了等式1b($\mathcal{X}$-transformation)。

算法1中的第1-3行中，将邻域点都归一化到点$p$的相对位置上，从而获得局部特征。在输出特征时，需要邻域点和对应的特征一起确定，但是局部坐标的维度和表示与对应的特征不一样。为了解决这个问题，首先将坐标提升到更高的维度上和更抽象的表示(如算法1的第2行所示)，然后将其与对应的特征进行拼接(算法1的第3行)，用于后面的处理(图3 c)。

通过point-wise $ML{P}_{\delta }(\cdot )$将坐标映射为特征，这与PointNet中使用的方法相似，不同之处就是没有使用对称函数进行处理。本文通过$\mathcal{X}$-transformation对坐标和特征进行赋权和排序，这个$\mathcal{X}$-transformation是通过所有的相邻点共同学习得到的。最终的$\mathcal{X}$依赖于点的顺序，这是期望的，因为$\mathcal{X}$应该根据输入点排列对${\mathbf{F}}_{\ast }$进行排序，因此必须知道特定的输入顺序。对于没有任何附加特性的输入点云，即$\mathbf{F}$为空，第一个$\mathcal{X}$-Conv层只使用${\mathbf{F}}_{\delta }$。因此，PointCNN可以以鲁棒通用的方式处理有或没有附加特性的点云。
$\mathcal{X}$

PointCNN Architectures

Conv layers in grid-based CNNs 和 $\mathcal{X}$-Conv layers in PointCNN有两个方面不同：

1. 局部特征提取的方式不同($K\times K$ patches vs. 表示点附近的$K$个相邻点)
2. 从局部区域中学习的方式不同(Conv vs. $\mathcal{X}$-Conv)

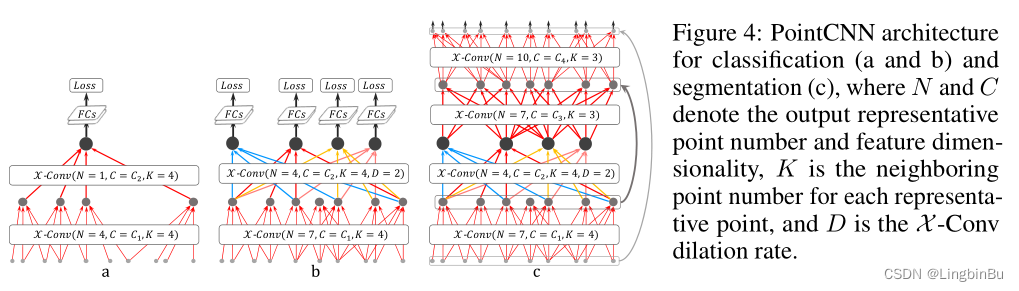
图4(a)描述了一个带有两个$\mathcal{X}$-Conv层的PointCNN结构，将输入点(带或不带特征)逐渐变成很少的表示点，但是这些点具有丰富的特征。在第二个$\mathcal{X}$-Conv层后，仅剩下一个表示点，这是从前面那些层中所有点的信息聚合在一起的表示点。在PointCNN中，可以将每个表示点的感知域定义为一个比例$K/N$，其中$K$是相邻点的数量，$N$是之前那一层中点的数量。这样，最后的那个点可以“看到”之前所有层的点，因此其感知域的比例为1.0——它具有整个形状的全局视野，并且其特征对于形状的语义理解也是信息非常丰富。在最后的$\mathcal{X}$-Conv层后面加上全连接层，接着跟一个损失函数便可训练这个网络。

我们注意到点的数量在上面的$\mathcal{X}$-Conv层中下降的很快(图 4a)，使得简单的网络无法全面地进行训练。为了解决这个问题，提出了带有稠密连接的PointCNN模型，如图4b所示。在$\mathcal{X}$-Conv层中保留了更多的表示点。但是，我们的目标是保持网络的深度不变，同时保持感知域的增长率，只有这样深层的表示点才能“看到”整个形状的更大区域。因此，在PointCNN中使用了从grid-based CNNs借鉴而来的dilated convolution思想。不再以固定的$K$个相邻点作为输入，而是随机的从$K\times D$个相邻点中随机采样出$K$个输入点，其中$D$是 dilation rate。在这种情况下，在没有增加实际相邻点总数的和kernel大小的情况下，感知域比例从$K/N$增长到$(K\times D)/N$。

与图4a相比，图4b中最后的$\mathcal{X}$-Conv层中的4个表示点都可以“看到”整个形状，因此都适合用于做预测。在测试阶段，softmax之前可以将多个预测结果取平均数，使预测结果更加稳定。

对于分割任务，需要输出原分辨率的点，这可以通过构造Conv-DeConv结构实现，其中DeConv部分就是将全局信息传播到更高分辨率预测的过程，见图4c。值得注意的是，PointCNN分割网络中的“Conv” 和 “DecConv”都是相同的$\mathcal{X}$-Conv操作。“Conv” 和 “DeConv”之间唯一不同的便是后者的输出具有更多的点，更少的通道数。

在最后的全连接层前面使用dropout减少过拟合现象，还使用了subvolume supervision进一步减少过拟合。在最后的$\mathcal{X}$-Conv层中，感知域比例被设置为小于1的数，以便于仅有部分信息被表示点观察到。在训练过程中，该网络被要求更艰难地从部分信息中学习，这样在测试时就会表现得更好。在这种情况下，表示点的全局坐标很重要，因此通过$ML{P}_g(\cdot )$将全局坐标提升到特征空间${\mathbb{R}}^{C_g}$，并拼接到$\mathcal{X}$-Conv中，以便通过后续层进行进一步处理。

Data augmentation

为了提高泛化性，提出对输入点进行随机采样和shuffle，这样batch与batch间相邻点集和顺序就会不一样。为了训练一个数量为$N$的点作为输入，选择$\mathcal{N}(N,(N/8{)}^2)$个点用于训练，其中$\mathcal{N}$表示高斯分布，这样做对于PointCNN的训练至关重要。

实验

Classification

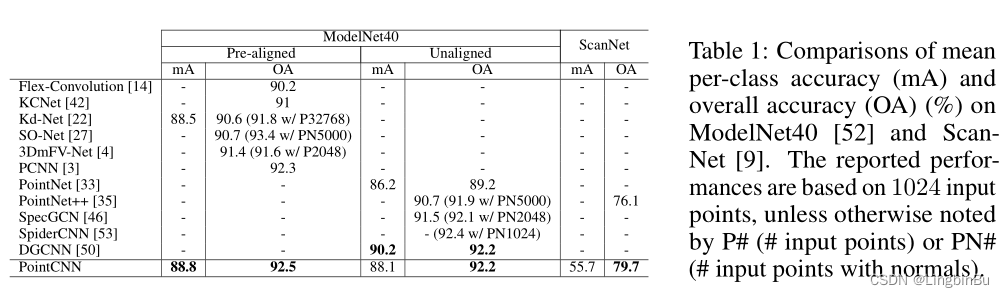
Segmentation

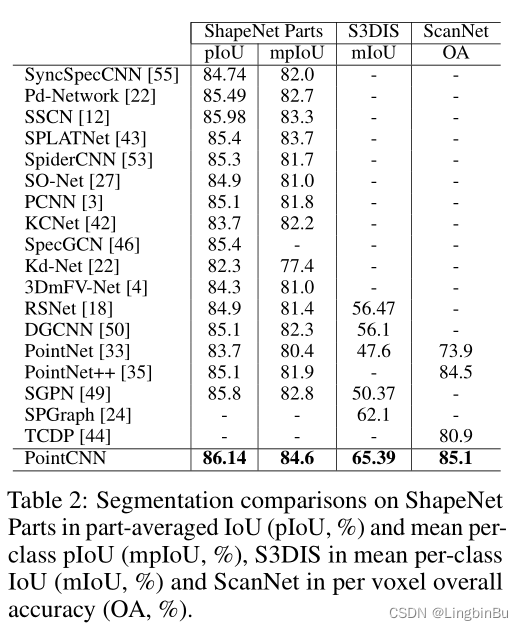
Ablation Experiments

Visualizations

Optimizer, model size, memory usage and timing

结论

• 如何理解提出网络的有效性还是一个很大的问题
• 将PointCNN 与 imageCNN结合起来处理成对的点云和图像也是一个很有趣的领域