牛顿法 主要有两方面的应用:
1.求方程的根;
2.求解最优化方法;
一. 为什么要用牛顿法求方程的根?
问题很多,牛顿法 是什么?目前还没有讲清楚,没关系,先直观理解为 牛顿法是一种迭代求解方法。
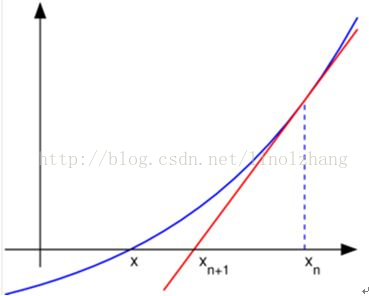
假设 f(x) = 0 为待求解方程,利用传统方法求解,牛顿法求解方程的公式:
f(x0+Δx) = f(x0) + f′(x0) Δx
即 f(x) = f(x0) + f′(x0) (x-x0)
公式可能大家会比较熟悉,一阶泰勒展式,f′(a) 表示 f(x) 在 x0 点的斜率 (这个很好理解),当X方向增量(Δx)比较小时,Y方向增量(Δy)可以近似表示为 斜率(导数)*X方向增量(f′(x0) Δx) ,令 f(x) = 0,我们能够得到 迭代公式:
x = x0 - f(x0) / f′(x0) => xn+1 = xn - f(xn) / f′(n)
通过逐次迭代,牛顿法 将逐步逼近最优值,也就是方程的解。
二. 扩展到最优化问题
这里的最优化 是指非线性最优化,解非线性最优化的方法有很多,比如 梯度下降法、共轭梯度法、变尺度法和步长加速法 等,这里我们只讲 牛顿法。
针对上面问题进行扩展:
解决 f(x) = 0 的问题,我们用了一阶泰勒展开:
f(x) = f(x0) + f’(x0)*(x-x0) + o( (x-x0)^2 )
去掉末位高阶展开项,代入x = x0+Δx,得到:
f(x) = f(x0+Δx) = f(x0) + f′(x0) Δx
那么 要解决 f′(x) = 0 的问题,我们就需要二阶泰勒展开:
f(x) = f(x0) + f’(x0)(x-x0) + 0.5*f”(x0)(x-x0)^2 + o( (x-x0)^3 )
去掉末位高阶展开项,代入x = x0+Δx,得到:
f(x) = f(x0+Δx) = f(x0) + f′(x0)Δx + 0.5 * f′′(x0) (Δx)^2
求导计算: f′(x) = f’(x0+Δx) = 0,得到:
[ f(x0) + f′(x0)(x−x0) + 0.5 f′′(x0)(x−x0)^2 ]′ = 0
整理:
f′(x0) + f′′(x0)(x−x0) = 0
x = x0 − f′(x0) / f′′(x0) => xn+1 = xn - f’(xn) / f’′(xn)
牛顿法 一图总结为:

三. 牛顿法 与 Hessian矩阵的关系
以上牛顿法的推导 是针对 单变量问题,对于多变量的情况,牛顿法 演变为:
与上面的单变量表示方式类似,需要用到变量的 一阶导数 和 二阶导数。
其中 J 定义为 雅克比矩阵,对应一阶偏导数。
H 为 Hessian矩阵,对应二阶偏导数。
牛顿法 在多变量问题上仍然适用迭代求解,但Hessian矩阵的引入增加了复杂性,特别是当:
▪ Hessian 矩阵非正定(非凸)导致无法收敛;
▪ Hessian 矩阵维度过大带来巨大的计算量。
针对这个问题,在 牛顿法无法有效执行的情况下,提出了很多改进方法,比如 拟牛顿法(Quasi-Newton Methods)可以看作是牛顿法的近似。
拟牛顿法 只需要用到一阶导数,不需要计算Hessian矩阵 以及逆矩阵,因此能够更快收敛,关于 拟牛顿法 这里不再具体展开,也有更深入的 DFP、BFGS、L-BFGS等算法,大家可以自行搜索学习。
总体来讲,拟牛顿法 都是用来解决 牛顿法 本身的 复杂计算、难以收敛、局部最小值等问题。
下面使用TensorFlow并且使用黑塞矩阵来求解下面的方程:
代码如下:
#python 3.5.3 蔡军生
#http://edu.csdn.net/course/detail/2592
#
import tensorflow as tf
import numpy as np
def cons(x):
return tf.constant(x, dtype=tf.float32)
def compute_hessian(fn, vars):
mat = []
for v1 in vars:
temp = []
for v2 in vars:
# computing derivative twice, first w.r.t v2 and then w.r.t v1
temp.append(tf.gradients(tf.gradients(f, v2)[0], v1)[0])
temp = [cons(0) if t == None else t for t in temp] # tensorflow returns None when there is no gradient, so we replace None with 0
temp = tf.stack(temp)
mat.append(temp)
mat = tf.stack(mat)
return mat
x = tf.Variable(np.random.random_sample(), dtype=tf.float32)
y = tf.Variable(np.random.random_sample(), dtype=tf.float32)
f = tf.pow(x, cons(2)) + cons(2) * x * y + cons(3) * tf.pow(y, cons(2)) + cons(4)* x + cons(5) * y + cons(6)
# arg1: our defined function, arg2: list of tf variables associated with the function
hessian = compute_hessian(f, [x, y])
sess = tf.Session()
sess.run(tf.global_variables_initializer())
print(sess.run(hessian)) 输出结果:
四、hession矩阵 边缘检测以及边缘响应消除
既然检测到的对应点确认为边缘点,那么我们就有理由消除这个边缘点,所以边缘检测与边缘响应消除的应用是一回事。边缘到底有什么特征呢?如下图所示,一个二维平面上的一条直线,图像的特征具体可以描述为:沿着直线方向,亮度变化极小,垂直于直线方向,亮度由暗变亮,再由亮变暗,沿着这个方向,亮度变化很大。我们可以将边缘图像分布特征与二次型函数图形进行类比,是不是发现很相似,我们可以找到两个方向,一个方向图像梯度变化最慢,另一个方向图像梯度变化最快。那么图像中的边缘特征就与二次型函数的图像对应起来了,其实二次型函数中的hessian矩阵,也是通过对二次型函数进行二阶偏导得到的(可以自己求偏导测试下),这就是我们为什么可以使用hessian矩阵来对边缘进行检测以及进行边缘响应消除,我想大家应该明白其中的缘由了。还是那句话,数学模型其实就是一种反映图像特征的模型。
所以Hessian matrix实际上就是多变量情形下的二阶导数,他描述了各方向上灰度梯度变化,这句话应该很好理解了吧。我们在使用对应点的hessian矩阵求取的特征向量以及对应的特征值,较大特征值所对应的特征向量是垂直于直线的,较小特征值对应的特征向量是沿着直线方向的。对于SIFT算法中的边缘响应的消除可以根据hessian矩阵进行判定。
参考:
http://blog.csdn.net/linolzhang/article/details/60151623
http://blog.csdn.net/caimouse/article/details/60465975
http://blog.csdn.net/lwzkiller/article/details/55050275










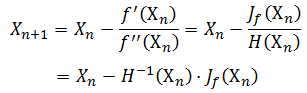
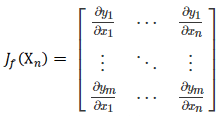


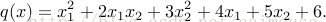
















 842
842











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








