Intel金融加速卡计算库及FPGA期权定价应用

作者：喻伟 东方证券FPGA加速应用负责人 / 黄琦 Intel FPGA金融加速产品经理
联系邮箱：yuwei1119@sina.com.cn / 个人微信号：yuwei_1119

近年来，在互联网、大数据、人工智能和云计算为代表的现代科技迅猛发展下，金融科技成为新时代金融创新的核心驱动因素。然而，金融科技在带来发展机遇的同时，也伴随着很大的挑战。FPGA以其高效灵活、低延时、可重复编程、低功耗，以及在高速计算领域的优异特性正在为解决金融科技的挑战带来新机遇。基于英特尔 FPGA的硬件加速器可显著改善金融工作负载的性能、加快算法的执行速度，高效赋能金融行业应用。

首先是Intel基于Arria 10和Stratix 10芯片设计的加速卡，如上图所示。

另外，也有智能网卡的产品，相较于通用网卡，Arria 10GT增加了以太网控制芯片和DPDK软件包的支持，同时DX210这张卡增加了对HBM高内存的支持，我们的应用场景，对数据报文转发，高带宽并发内存有需求，可以考虑这张卡。

然后是Intel最新发布的IPU C5020，其重要的核心功能是，在卡上单独放置了一块Xeon D CPU，因此很多潜在的需要CPU参与的金融计算都可以offloading到这张卡上，从而避免了通过主机PCIE与主板CPU的交换延时。

如果以上硬件板卡依然无法满足你对于定制化的硬件平台的需要，那么通过Intel开放式FPGA加速堆栈，你可以方便的开发出一款新的硬件板卡，快速部署相关的底层FPGA接口和软件驱动的设计。

另外，Intel发布了OneApi统一编程框架，可以对CPU、GPU、FPGA等不同的硬件平台，使用同一种DP C++语言进行统一编程，并且可以快速的将传统基于CPU的算法移植到FPGA上，并且通过Vtune Profile工具进行优化，从而获得不错的加速效果，OneApi编程语言和开发工具大大降低了FPGA的开发门槛，加快了金融解决方案的开发和部署。

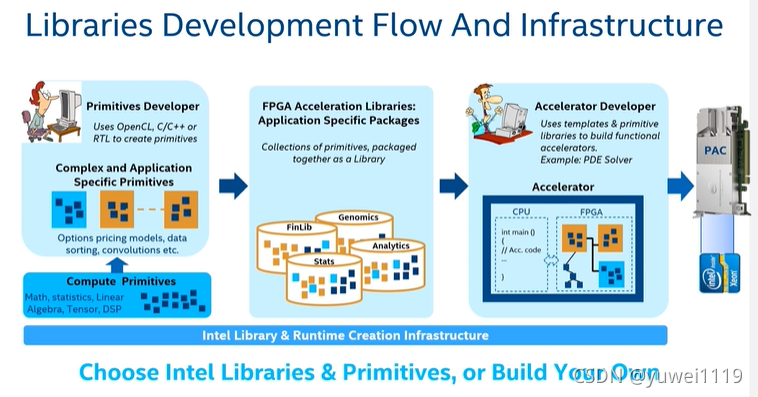
同时，为了提高加速效果，降低开发难度，Intel还专门用于金融计算的FPGA加速库，其设计思想是通过效率更高的RTL或HLS语言，对基本金融计算算子金融优化设计，并将其包装成库，C++程序员通过调用库函数，从而能够方便的完成一个基于应用软件的开发，兼顾了效能和开发的便捷性。下面重点介绍一些基于FPGA的金融加速库。

金融加速库包含了三个层面的内容和代码，最底层是与金融计算相关的金融算子，例如日期工具，线性代数的计算，随机数发生器，统计类函数以及期权类函数，另外还包含了大量的数学计算算子，这些已经由Intel开发完成并进行了充分的优化，应用程序员只需调用即可。

在此基础上，我们提供了一些代码教程，演示如何调用基本算子，完成一些简单的计算，比如矩阵计算，日期的处理，以及BS默顿方程和相关希腊值的计算。

最后是基于实际应用产品的参考设计，包括了诸如解偏微分方程，基于CRR二叉树模型的美式期权定价和相关希腊值的计算，基于蒙特卡罗模拟的各种奇异期权的定价，以前的历次分享都主要注重对FPGA设计优化方法的介绍，忽略了对基本金融算法的讨论，实际上，对于大部分FPGA开发者和软件工程师而言，花一点时间了解金融理论对于我们理解代码进而优化性能更有帮助。

首先了解一下Intel Finlib中，有关布莱克-斯科尔斯公司的参考设计。

Black-Scholes1973年发表的关于期权定价的模型，被誉为金融衍生品定价的基石。1997年Scholes和Merton凭借该模型获得了诺贝尔经济学奖。BS模型假设金融市场中，存在至少一种风险资产，比如股票，以及一种无风险资产、现金或者债券，那么对于假设的金融资产，它具有如下特性：(1)无风险资产的投资回报率是不变的，此回报率被称为无风险利率。(2)股票的价格遵循几何布朗运动。(3)股票在期权的有效期内，并不分派红利，股票的价格服从对数正太分布。他们同时假设，金融市场是不存在套利机会的，并且能以无风险利率借入或者借出任意数量的金钱，能够买入或者卖出任意数量的股票，假设市场是无摩擦的，即不存在交易税收和交易成本，因此在这种假设下面，可以通过该方程计算欧式期权，所谓欧式期权，是只可以在特定日期内行权的一种期权。

首先我们假设，股票的运行遵从一个几何布朗运动，drift trem代表了股票的长期趋势，volatility term代表了股票的短期波动，日本的数学家伊藤清，他提出了一个对于随机过程函数作微分的法则，根据该法则，对于一个时间依赖的随机变量，股票的价格可以表示为上面的公式，在这个公式中，u代表了股票的期望收益率，而德尔塔代表了股票的波动率，w代表了某种未知因素。

股票长期趋势，短期波动以及叠加后的走势，可以分别使用这些公式和图形表示。

BS基于股票价格和布朗运行的假设，得到了股票期权相对股票现货价格以及行权时间所应遵从的偏微分方程，在这里V代表了期权的价格，而S代表了现货的价格，因此这个方程是关于S和t的二阶偏微分方程。

BS提出了上述偏微分方程的公式解及根据该公式可以算出的看涨期权和看跌期权的价格，这个公式当作，S代表了股票的现货价格，而K代表了期权的行权价格，R表示无风险利率，t代表到期时间，西格玛代表标的物的波动率，而N指出它是一个正太累计分布。这个公式，在很多情况下，会被使用者改正和修正。经验表面，这个公式足够贴近真正的市场价格。

默顿，引入了一个变量持有成本，因此，这个公式，又被改进到如上样子。

在此基础上，我们还可以计算一些欧式期权的希腊值，这些希腊值代表了一些特定的含义，比如说德尔塔是期权价格相对于标的资产的一阶导数，即股票市场每变化一个单位期权价格变化的幅度，伽马是期权价格相对于标的资产变化的二阶导数，代表了德尔塔相对股票价格的变动率，也就是股票价格变化一个单位，德尔塔值变化的幅度，伽马衡量的是德尔塔相对于股票价格的敏感程度，theata代表时间流逝对于期权价格的变化，即每减少一天，期权价格的变化值，比如对于看涨期权的价值，它随日期成反比，越接近到期日，期权作为对冲工具的价值就越小，vega代表了波动率单位变动对于期权价格的影响，因为波动率经常用百分百表示，因此vega每变动1%对于期权价格的影响，BS公式及相关希腊值的计算可以作为一个参考设计在Intel的工程中找到，可以基于仿真环境或者A10或S10真实板卡运行。

二叉树模型，即CRR模型，其核心思想是，股票的价格，在每个时点，都会以某个概率向上或者向下运动，通过二叉树方式，构建现价到行权到期日之间可能的价格分布，并反推现实期权的理论价格，假设已知股票价格的波动为西格玛，那么一段时间德尔塔t以后，股票价格上涨或者下跌的幅度可以按照此公式得到。

那么Step1，我们假设现在股票的价格为45，波动率为20%，西格玛为0.2，那么进行最简单的估计，我们可以将步长设定为1，德尔塔t等于1.5，那么根据上面所提到的公式，我们可以得到一年半以后股价最高可能到57.49，最低可能到35.22.

如果想得到更加精细的估计，那么我们可以增加步数到3倍，步长减小到0.5，这样我们可以得到一个三级的二叉树，并且得到各个节点的价格。

那么Step2，我们得到所有节点的股票价格后，还需要知道股价有多大概率运行到某一个价格节点，我们知道期权是用来对冲股票价格未知波动的，合理的期权价格应该是构建一个资产组合，无论期权价格是上下波动还是向下波动，股票和期权的组合的期望收益率都只是无风险利率，据此我们可以推断，向上变化概率乘以向上价格变动幅度，加上向下变化概率乘以向下价格变动幅度，等于无风险利率。因此，在给定无风险利率的情况下，可以计算向上或者向下概率。

按照此公式，可以计算出股票价格向上或者向下变动的概率。
那么Step3，我么们可以来计算按照这样的股价运行方式下期权的收益，所谓期权的收益，它是假设行权价格等于初始股票价格，而行权的收益等于行权价，在这个时候，标的物的即时价假设为一个确定的值，那么收益就等于行权价-标的物的即时价。如果值为负，那么收益为0，投资者选择不行权；如果为正，那么相应的差值即为行权收益。

那么Step4，将可能的行权收益乘以其运行概率，并将其折现，即可得到上一个节点的期权收益。比如说上图，从最后一个行权日反推计算，因为按照最上面两种价格走势趋势，我们的行权收益为0，所以上面的上一个阶段没有期权收益，那么下面的两个，其价格分别乘以向上和向下概率，再折现，就可以得到这个节点行权收益的折现价格是9.98.

那么以此类推，可以得到当前初始节点的期权价格。这个例子是基于欧式期权，相对比较简单，因为所有的节点都不用考虑提前行权的可能性。


对于美式期权，相对于欧式期权的特别之处在于，在每个节点都可以提前行权，在计算每个节点的价格时，要比较一下是现在行权还是持有到期行权，比如说，股票价格达到33.91时，提前行权的收益为11.09，而持有到期的收益为9.98，选择较大的行权收益为该节点的期权价格。这是按照上述步骤模拟的美式期权的价格，我们可以看到，美式期权的价格高于欧式期权的价格。如果说期权价格是对于未来不确定性的估值，那么这个结果是合理的，因为美式期权的选择权更多了，通过解释二叉树进行期权定价的原理，我们可以看到，在第一步构造二叉树的时候，前后的计算具有时序依赖性，但是一旦二叉树构建完成，在反向计算期权的行权价值时，各条路径之间具有并行性，并且通过优化流水线结构，在完成真个计算的时候使用FPGA，具有较大的并行优势。

蒙特卡洛模拟是一种使用更为广泛的数值计算方法，使用蒙特卡洛计算期权价格，其基本思想是，从现在的股票价格出发，模拟大量可能的股价运行路径。

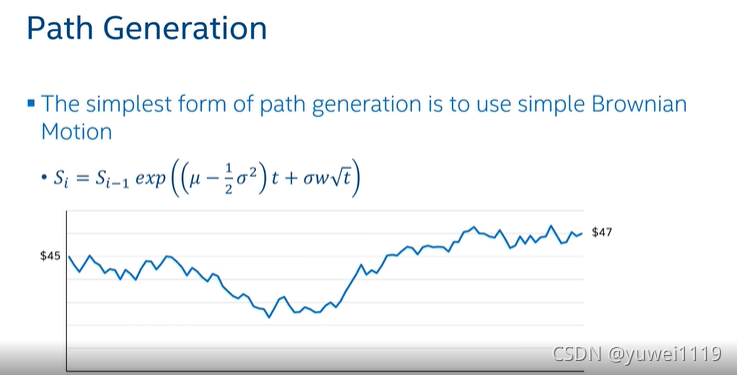
股价的运行路径依旧可以根据布朗运行来表达。

那么得到模拟后股价后，可以根据现在的股价的spot值和行权价格，我们可以得到看涨期权的收益，payoff等于股票价格减去行权价格，在这个例子中，它的行权收益为2。

那么如果股票的终止价格低于行权价格，投资者可以不行权，因此针对很多条不同的股价运行路线，我们可以得到它的行权收益。

那么将所有可能路径下的未来时点收益进行平均，得到一个平均收益，将其折现，这就是现在期权的价格，比如说一年半以后的行权收益为2.08元，在无风险利率为5%的情况下，折现到现在，现在的期权价格就应该为1.93.

实际上可以处理更多复杂的模型，比如说随机数的产生和分布，相关性需要考虑一揽子期权和点差，对于很多奇异期权，路径依赖期权计算行权收益的时候，并非只有一个固定的方法，对于路径的产生函数，也有很多不同的方法。总的来说，蒙特卡罗方法，各条路径之间是相互独立的并且具有并行性，最终的模拟结果和模拟次数正相关，模拟次数越多，结果越准确，对某些特定的算法，模拟次数一定要达到一定的规模，其结果才是收敛的。FPGA非常适合各类需要蒙特卡洛计算的金融场景。

其它，我们做个小结：(1)BS公式可以提供欧式期权的解析解，简单，快速，使用CPU即可完成.(2)二叉树或者CRR方法，对固定波动率假设下美式期权的计算有优势.(3)PDE和Quadrature对于解决真实波动率，行权条件比较复杂个各种奇异期权比较有优势，提供了在更高维度解决奇异期权的方案.(4)蒙特卡罗模拟通过简单的数值模拟可以解决各种复杂的资产定价问题。他们计算的复杂度和使用纯软件方法相比，依次增加，对于并行度较好的算法，使用FPGA计算效果较为明显。