基于交叉表生成风控规则（Python）

大家好，我是东哥。

规则是风控策略中最常用的工具之一，生成、筛选、监控、调优，几乎每天都在打交道，本篇来介绍如何基于交叉表来生成风控规则，并且如何基于评估指标进行筛选。

出品人：东哥起飞

专栏：《100天风控专家》

1.1. 交叉表的概念

什么是交叉表？

交叉表，顾名思义，就是两个或者两个以上的变量进行交叉判断。

比如下面这个示例，一个变量是“最近6个月新开信贷账户数”，另一个变量是“当前公积金状态”，这就是两个变量的交叉表形式，也叫“二维交叉表”，如果是两个以上的变量就是“多维交叉表”。

交叉表的形成，本质上就是变量的“笛卡尔积”。

1.2. 交叉表的特点

交叉表有什么特点？

按照规则的复杂度和数据维度两个角度来看，交叉表规则处于单变量规则和评分卡模型之间的中间形态。

• 与单变量规则相比，交叉表拥有更多的维度，对于客户风险评估更加准确。
• 与评分卡模型相比，交叉表虽变量维度少，但复杂度更低，迭代开发速度更快。
• 在所有的工具中，交叉表属于一种中间的形态，同时兼顾了维度和复杂度两点。

1.3. 交叉表的前置条件

要生成二维交叉表，有3个前提条件：

1）基于IV筛选出预测效果好的变量池，从中选择交叉所需的变量组。

一般的原则是：交叉变量最好是不同维度的，且相互间的相关性不高，这样综合效果才会达到最优。

2）对变量进行分箱操作，连续型变量需要有排序性；

仍以下面的二维交叉表为例，我们看到“最近6个月新开信贷账户数”是连续型变量，“当前公积金状态” 是离散性变量。这里公积金状态有三个离散值，因此不需要分箱；而最近6个月新开账户数由于是连续型变量，是需要做分箱处理的。

3）总样本和坏样本数量足够多。

交叉表通过两两组合，有更多的格子。比如下面一维变量只有4个格子，而二维交叉表有12个格子，而总数量和总坏客户数是相同的，那么经过稀释后交叉表的每个格子数据量会变少。如果总样本数和坏客户数不够的话，那么分散到每个格子的数量就可能出现过少，或者没有数据的情况，导致无统计意义无法分析。因此如要保证每个格子都有足够的数据，总样本和坏样本数就必须足够多。

二、交叉表规则生成与评估

2.1. 三个步骤

交叉表规则制定一般有以下三个步骤：

2.2. 交叉表规则生成(1)：透视表

2.3. 交叉表规则生成(2)：计算指标

区间坏账率=每个格子的坏客户数/对应格子的总客户数，是上下两个交叉表每个格子对应位置的计算，比如蓝色框示例，4.43%=19/429；

客户占比=每个格子的客户数/总客户数，只需总客户数一个交叉表即可，比如红色框示例，3%=59/1967；

2.4. 交叉表规则生成(3)：制定和评估

三、交叉表应用场景

3.1. 策略D类调优

1）背景介绍

某机构发现，近期市场环境不好，客户的贷后逾期率不断升高，业务部门提出需求：需要风控策略人员对贷前审批策略进行收紧，降低逾期风险，但同时不降低太多通过率，因为业务规模是本年的考核指标。

2）策略方案

该需求属于策略D类调优。可新增二维交叉表规则，比如右侧这条规则，命中率仅为1.68%，但拒绝客户中一半以上都是坏客户。

如果使用单变量规则，比如最近6个月新开信贷账户数>=3时拒绝，区间坏账率为25.47%，命中率则为8.19%，会降低很大通过率 。

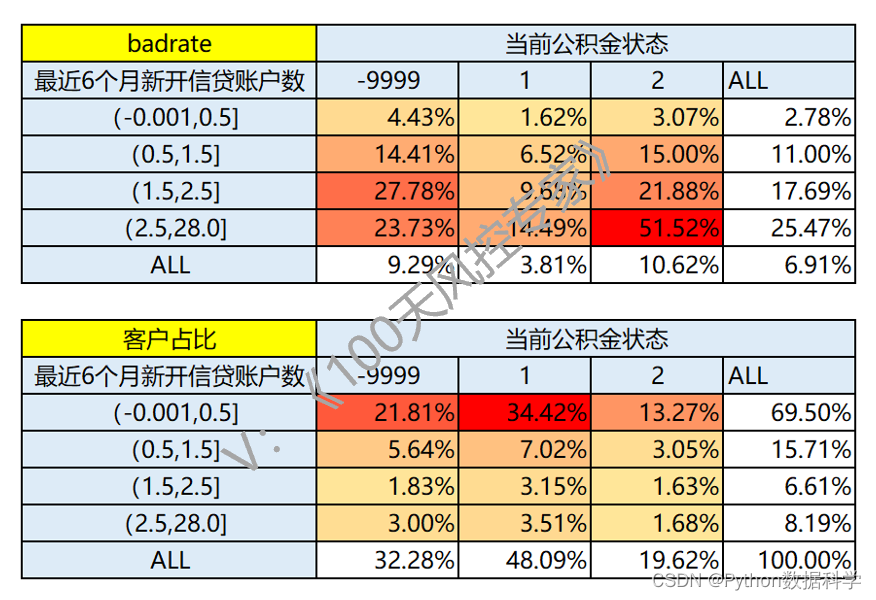
二维交叉表规则：“最近6个月新开信贷账户数在(2.5,28]之间”且“当前公积金状态为2”，触发则拒绝，反之通过。

---

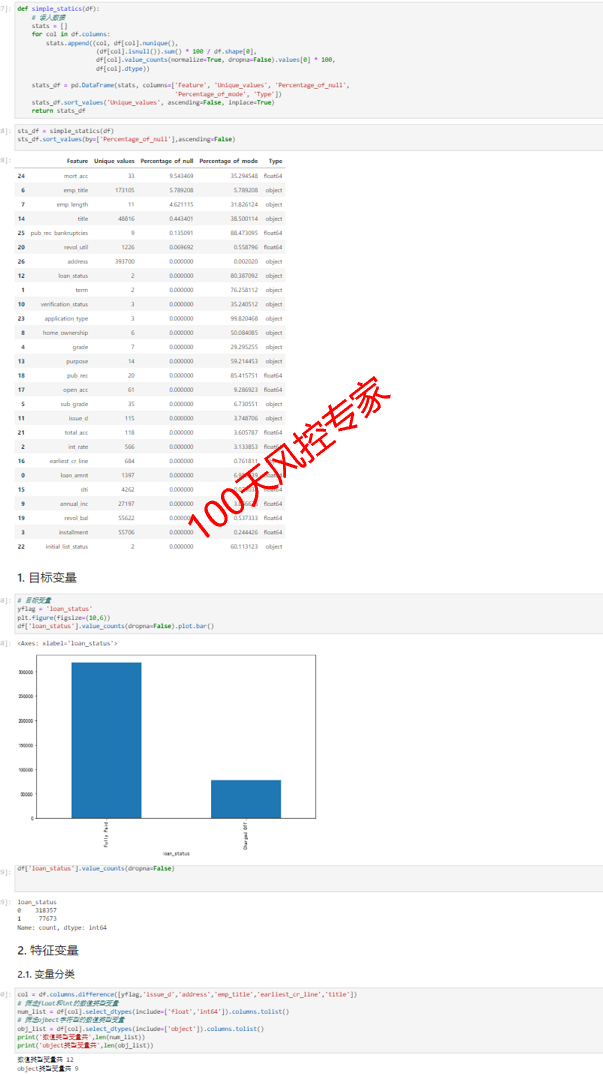
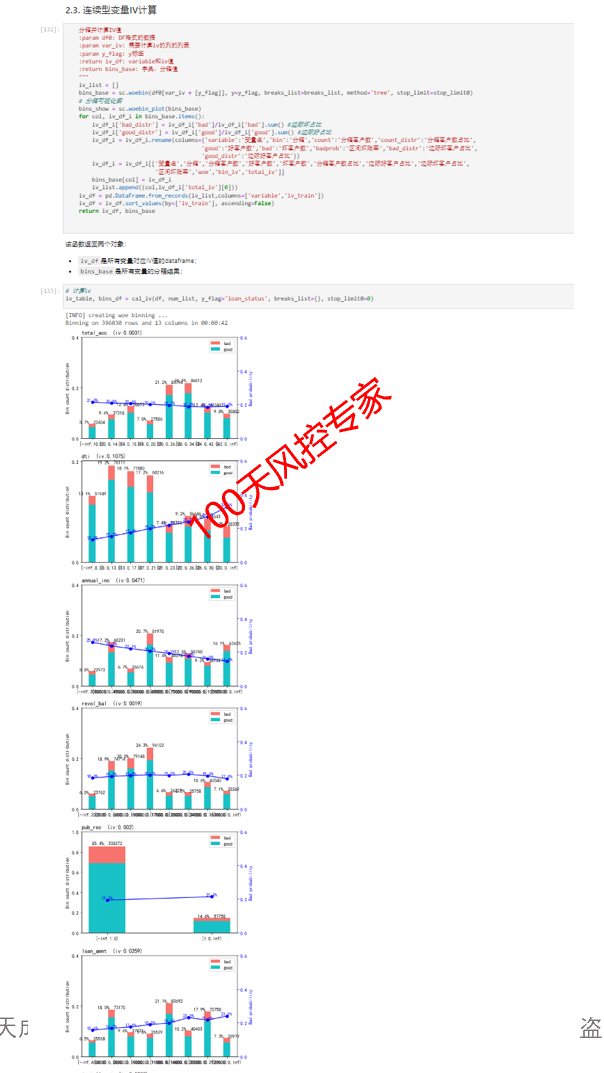
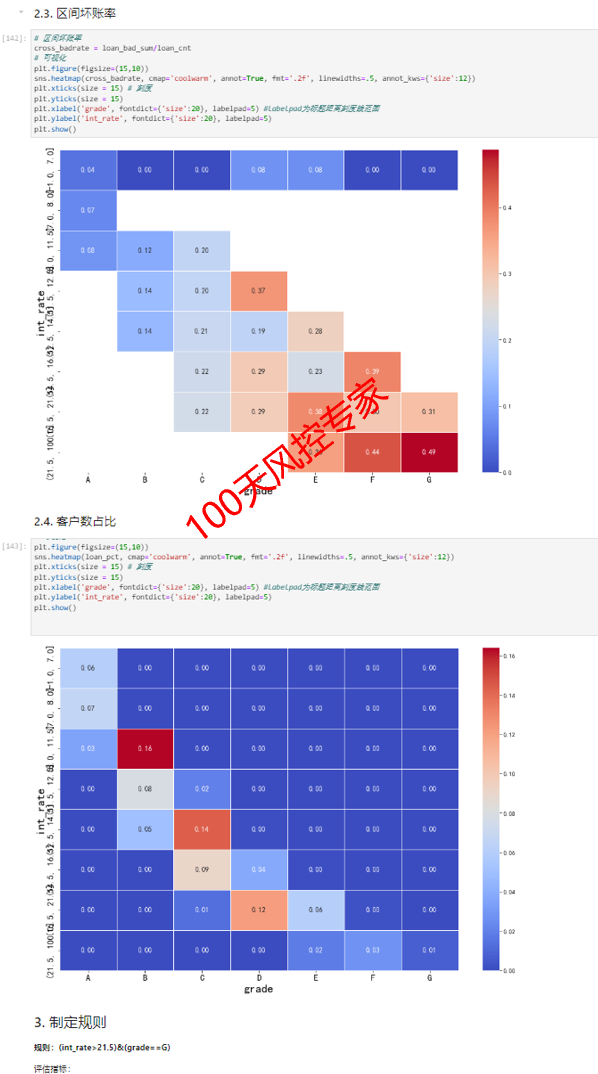
以下是基于交叉表生成规则的Python的实战案例部分。

<,,,,,>

以上来自原创专栏《100天风控专家》规则篇分析全流程的节选内容，共100期以上视频更新，包括业务、产品、策略、模型、数据、系统6大核心模块，理论+Python代码实操，从零到一入门金融数据风控。规则篇课件内容如下。