改善深层神经网络(吴恩达)_优化算法

本篇主要会谈到：mini-batch梯度下降、指数加权平均、动量梯度下降、RMSprop、Adam优化、学习率衰减

---

mini-batch梯度下降：

在前面学习向量化时，知道了可以将训练样本横向堆叠，形成一个输入矩阵和对应的输出矩阵：

$X=\left [x^{(1)},x^{(2)},x^{(3)}...x^{(m)}\right ]$
$Y=\left [y^{(1)},y^{(2)},y^{(3)}...y^{(m)}\right ]$

当数据量不是太大时，这样做当然会充分利用向量化的优点，一次训练中就可以将所有训练样本涵盖，速度也会较快。但当数据量急剧增大，达到百万甚至更大的数量级时，组成的矩阵将极其庞大，直接对这么大的的数据作梯度下降，可想而知速度是快不起来的。故这里将训练样本分割成较小的训练子集，子集就叫mini-batch。例如：训练样本数量m=500万，设置mini-batch=1000,则可以将训练样本划分为5000个mini-batch，每个mini-batch中含有1000个样本数据，当然，输出矩阵也要做同样的划分。这张图可以直观的理解：

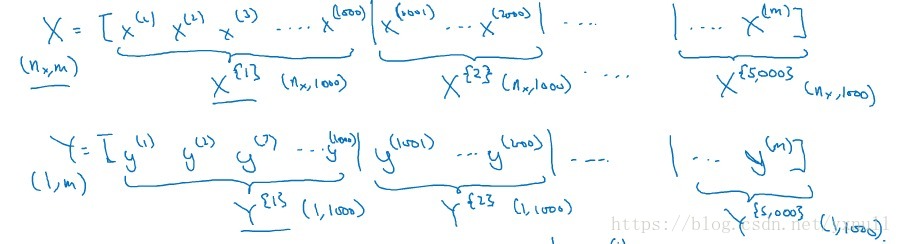
在实际的训练中，会通过循环来遍历所有的mini-batch，对每一个mini-batch都会做和原来一样的步骤，即：前向传播、计算损失函数、反向传播、更新参数。

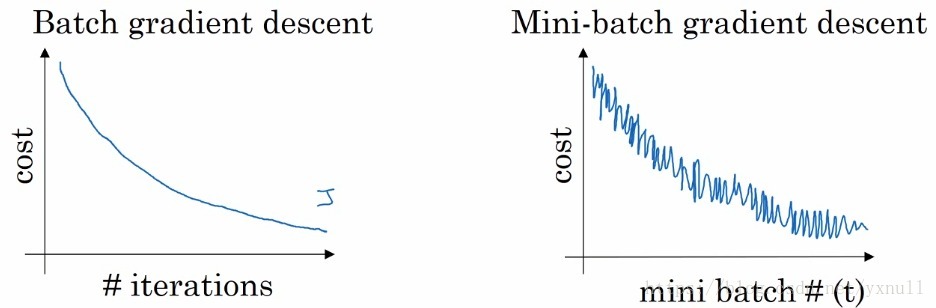
这张图可以大致反应两种梯度下降方法其损失函数的变化过程：在batch梯度下降中，由于每次训练迭代都是遍历的整个训练集，故损失函数的曲线应是一个较为平滑的下降过程，如出现明显的抖动，很大程度可能是学习率α过大。但在mini-batch梯度下降中可以看到，并不是每次迭代其损失函数都是下降的，这是因为训练集不完整的原因。但总体趋势还是下降的，抖动程度取决于设置的mini-batch的大小。
综合来说，如果训练集较小，那么直接使用batch梯度下降法，可以快速的处理整个数据集，一般来说是少于2000个样本。如果训练集再大一点，就可以考虑使用mini-batch梯度下降法，一般mini-batch的大小为64 - 512（考虑到电脑内存，设置为2的n次方，运算速度会快些）。另外，当mini-batch设置为1时，又叫做随机梯度下降法。

---

指数加权平均：

对于这个概念，视频课程中举了个这样的例子：下图是一年内某地气温的变化情况：

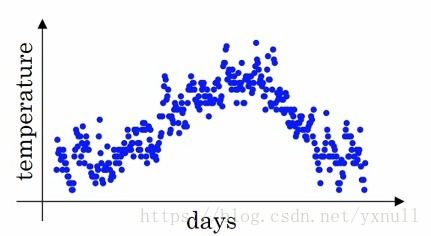
可以看到数据点比较的杂乱，但是大体趋势还是存在的。为了更好的表现气温变化情况，这里做一下这样的处理：

这就得到了指数加权平均值，用红线再次作图的话，可以得到如下图：

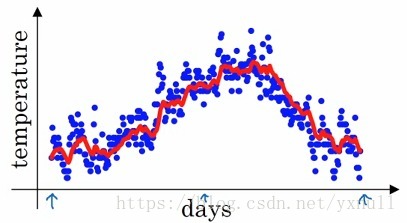
可以看到数据的抖动情况明显好转。在上面的公式中，将0.9看成$\beta$，则得到了通式$v_{t}=\beta v_{t-1}+(1-\beta )\theta _{t}$，可以这样理解，$v_{t}$表示$\frac{1}{1-\beta }$日的平均气温，例如当$\beta=0.9$时，$\frac{1}{1-\beta }=10$，则$v_{t}$表示的就是10天的平均温度。再如当$\beta=0.5$时，可知$v_{t}$表示的则是2天的平均温度，如下图的黄线：

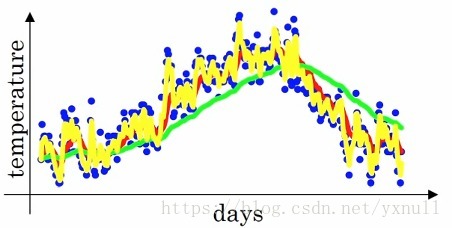
由于只平均了2天的气温，所以抖动程度还是很明显。下面即将谈到的几种梯度下降的优化算法都是基于这个指数加权平均数的思想。

---

动量梯度下降(Gradient descent with Momentum)：

简单的说，该算法的思想就是计算梯度的指数加权平均数，并利用该梯度更新权重参数。
下面这张图可以很好的帮助我们理解：

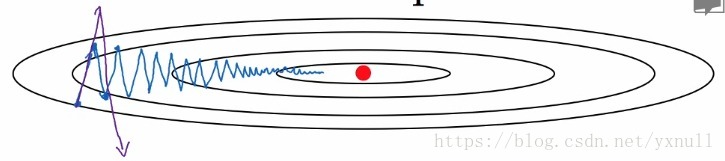
假设损失函数（或者叫成本函数）是上面的形状，红点表示其最小值，利用batch或mini-batch梯度下降，会不断的逼近最小值，如蓝线所示（紫线表示学习率$\alpha$选择的太大，波动太剧烈）我们理想情况波动尽量小，这不恰好可以利用上面说的指数加权平均嘛。具体做法是令

$v_{dw}=\beta \cdot v_{dw}+(1-\beta )\cdot dW$
$v_{b}=\beta \cdot v_{b}+(1-\beta )\cdot db$

然后重新赋值权重:

$w=w-\alpha \cdot v_{dw}$
$b=b-\alpha \cdot v_{db}$

关于动量梯度下降，我在CSDN上看到了一张很形象、很好理解的图，这里贴出来:

原文地址为： https://blog.csdn.net/tsyccnh/article/details/76270707

---

RMSprop

还是这张图，为了方便理解，横轴表示w，纵轴纵轴表示b。我们想要尽可能的加快横轴w方向的学习，而减少纵轴b方向的学习。和上面提到的动量梯度下降有一定的相似之处，令：

$S_{dw}=\beta \cdot S_{dw}+(1-\beta )(dw)^{2}$
$S_{db}=\beta \cdot S_{db}+(1-\beta )(db)^{2}$

更新参数时，也有一定的变化：

$w=w-\alpha \cdot \frac{dw}{\sqrt{S_{dw}}}$
$b=b-\alpha \cdot \frac{db}{\sqrt{S_{db}}}$

可以这样分析这个算法，在原始的梯度下降中，dw一般会较小，而db一般会较大，如上图所示，使用RMSprop后我们会发现，①式的结果$S_{dw}$是较小的，②式的结果$S_{db}$是较大的，分别带入③④中会发现w的变化程度较大，而b的变化程度较小，不刚好解决了b方向的波动太大，而w方向的进步太小的问题嘛。

---

Adam

Adam优化算法基本上就是将Monentum和RMSporp结合在一起，已被证明适用于不同的深度学习结构，能够很好的解决很多问题，下面具体看看Adam是怎么工作的，首先初始化：$V_{dw}=0,S_{dw}=0,V_{db}=0,S_{db}=0$,下面该Monentum和RMSprop上场了：

$V_{dw}=\beta_{1}\cdot V_{dw}+(1-\beta_{1})\cdot dw$
$V_{db}=\beta_{1}\cdot V_{db}+(1-\beta_{1})\cdot db$
$S_{dw}=\beta_{2}\cdot S_{dw}+(1-\beta_{2})(dw)^{2}$
$S_{db}=\beta_{2}\cdot S_{db}+(1-\beta_{2})(db)^{2}$

一般在使用Adam时，需要进行偏差修正（t为迭代次数）：

$V_{dw}^{corrected}=\frac{V_{dw}}{1-\beta _{1}^{t}}$
$V_{db}^{corrected}=\frac{V_{db}}{1-\beta _{1}^{t}}$
$S_{dw}^{corrected}=\frac{S_{dw}}{1-\beta _{2}^{t}}$
$S_{db}^{corrected}=\frac{S_{db}}{1-\beta _{2}^{t}}$

最后更新权重：

$w=w-\frac{\alpha \cdot V_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}}}$
$b=b-\frac{\alpha \cdot V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}}$

在这个算法中可以看到出现了很多超参数，其中学习率$\alpha$的取值很重要，需要经常调试，然后比较看看哪个最有效，$\beta _{1}$通常取0.9，至于超参数$\beta _{2}$，Adam论文的作者推荐使用0.999。

---

学习率衰减

加快模型学习速度的一个办法就是随时间慢慢减小学习率$\alpha$，我们称之为学习率衰减。

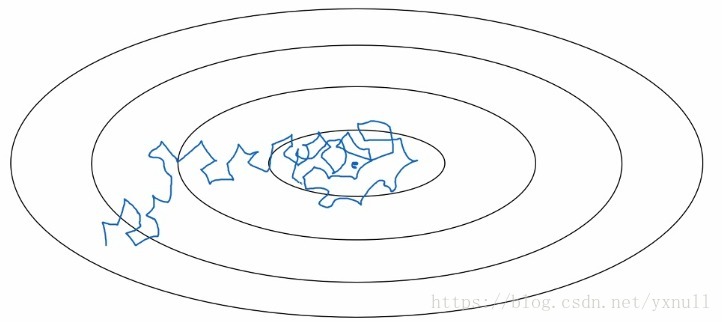
我们可以抽象的将学习率理解为每次前进的“步长”，当在减少成本函数的初期，大一点的学习率有助于更快的逼近最小值，可是到了后期，由于已经非常接近最小值，如果不改变学习率，即“步长”还是和原来一样，那么会在最小值附近出现明显的摆动。所以在模型训练的过程中，应该不断减小学习率的值，才能更好的到达成本函数的最低点。（这应该很好理解，类比高尔夫，球越接近洞口，每次移动的距离就应该越小）至于具体的衰减方式，有很多种，例如指数衰减、离散衰减。这里就不详细讨论。目的都是能够恰当的减小学习率，从而加快模型的学习速度。