Bicubic介绍及Python实现

Bicubic

Bicubic 介绍

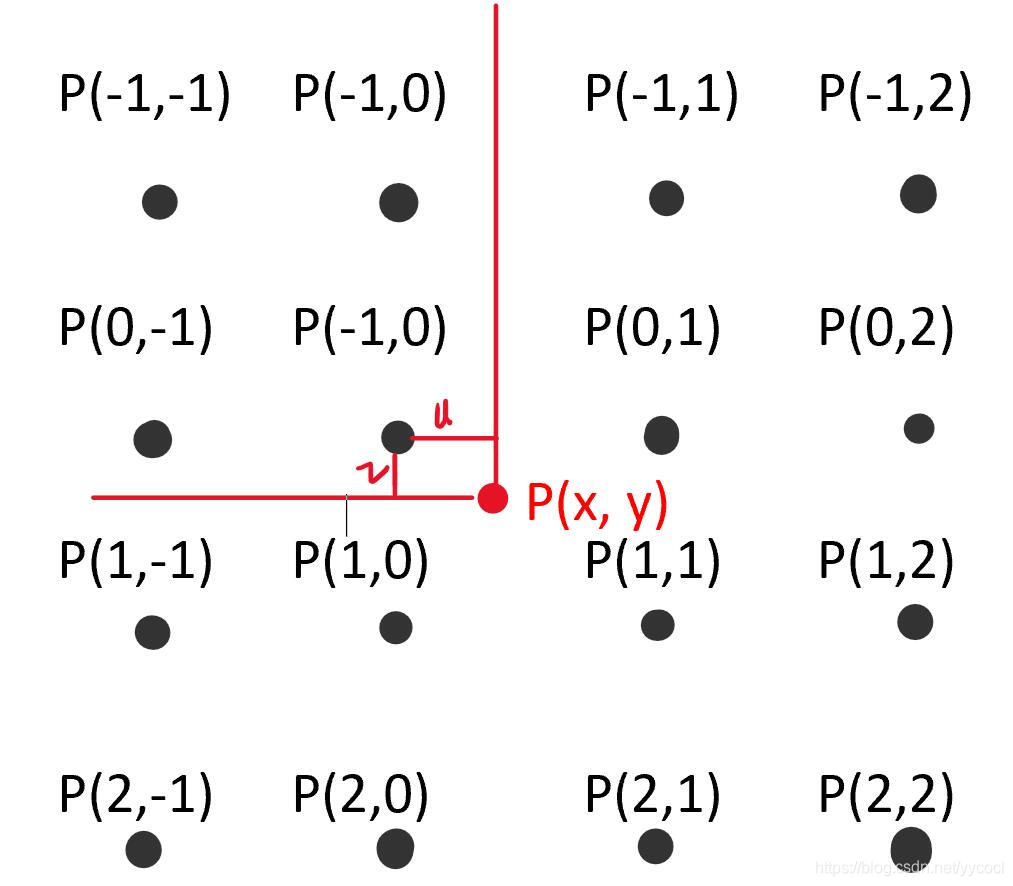
放大图像某点的像素值涉及其映射到原始图像一点的临近16个像素点。
在横、竖两个方向分别采用多项式插值三次函数

1.像素点

插值像素点与原图像的关系：

2.插值函数

插值函数是对于理论上最优插值函数$sin(x)/x$的近似。
函数如下，一般取a = -0.5
$$W(x)=\{\begin{array}{ll}(a+2)|x{|}^3-(a+3)|x{|}^2+1& |x|\le 1\\ a|x{|}^3-5|x{|}^2+8a|x|-4a& 1<|x|<2\\ 0& others\end{array}$$

3.像素值计算

对于每个像素点像素值的计算:
$$B(X,Y)=\sum _{n=-1}^2\sum _{m=-1}^{2}f(n+j,m+i)\times W(u-m)\times W(v-n)$$
矩阵计算方式如下:

$$\begin{array}{rl}& A=\left[\begin{array}{cccc}W(u+1)& W(u)& W(u-1)& W(u-2)\end{array}\right]\\ & C=\left[\begin{array}{cccc}W(v+1)& W(v)& W(v-1)& W(v-2)\end{array}\right]\\ & B=\left[\begin{array}{cccc}f(j-1,i-1)& f(j-1,i)& f(j-1,i+1)& f(j-1,i+2)\\ f(j,i-1)& f(j,i)& f(j,i+1)& f(j,i+2)\\ f(j+1,i-1)& f(j+1,i)& f(j+1,i+1)& f(j+1,i+2)\\ f(j+2,i-1)& f(j+2,i)& f(j+2,i+1)& f(j+2,i+2)\end{array}\right]\\ & f(j+v,i+u)=CB{A}^T\end{array}$$

bicubic python代码