1.同时抛一对质地均匀的骰子,也就是各面朝上发生的概率均为1/6。试求:
1)“3”和“5”同时发生这一事件的自信息量。
2)“两个1同时发生”这一事件的自信息量。
3)“两个点数中至少有一个是1”这一事件的自信息量。
解:1)设事件A:“3和5“同时出现
同时扔两个正常的骰子,可能的状态数有36种,36种状态中任一状态出现的概率相等,为1/36
在这36种状态中,3和5同时出现有两种情况,即3,5和5,3
P(A)=2*1/36=1/18
I(A)=-logp(A)=log218≈4.17bit
2)事件B:两个1同时发生
P(B)= 1/36,I(B)=-logp(B)=log36≈5.17bit
3)事件C:两个点数中至少有一个是1
事件D:两个点数中一个1也没有
p(D)=5/6*5/6=25/36
p(C)=1-p(D)=11/36
I(C)=-logp(C)=log2(36/11) ≈1.71bit
2.居住某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6M以上的,而女孩中身高1.6M以上的占总数的一半。假如我们得知“身高1.6M以上的某女孩是大学生”的消息,问获得多少信息量?
解:A:女孩是大学生 B:女孩身高1.6米以上
则:p(A)=25%,P(B)=0.5,p(B|A)=0.75,即求p(A|B)的自信息量。
p(A|B)=P(AB)/P(B)=P(B|A)*P(A)/P(B)
=0.75*0.25/0.5≈0.37
p(A|B)= -logp(A|B)=-log0.37=1.415bit
3.有两个二元随机变量X和Y,它们的联合概率分布函数如表所示:
同时定义另一随机变量Z=X•Y(一般乘积),试计算:
1)H(X),H(Y),H(Z),H(XZ),H(YZ),H(XYZ)
2)条件熵H(X|Y),H(Y|X),H(X|Z),H(Z|X),H(Y|Z),H(Z|Y),H(X|YZ),H(Y|XZ)和H(Z|XY)
3)互信息量I(X;Y),I(X;Z),I(Y;Z);I(X;Y|Z),I(Y;Z|X)和I(X;Z|Y)

解:1)求H(X),H(Y),H(Z),H(XZ),H(YZ),H(XYZ)
H(X)=log2=1bit/符号 H(Y)=log2=1bit/符号
H(Z)=5/8*log8/5+3/8*log8/3=0.9544bit/符号
2)条件熵H(X|Y),H(Y|X),H(X|Z),H(Z|X),H(Y|Z),H(Z|Y),H(X|YZ),H(Y|XZ)和H(Z|XY)
3)互信息量I(X;Y),I(X;Z),I(Y;Z);I(X;Y|Z),I(Y;Z|X)和I(X;Z|Y)
4.对于任意三个离散随机变量X,Y,Z,求证:
H(XYZ)=H(XZ)+H(Y|X)-I(Z;Y|X)
H(XYZ)-H(XY)≤H(ZX)-H(X)
证明:
1)H(XYZ)=H(XZ)+H(Y|X)-I(Z;Y|X)
根据熵的链规则有:
H(XYZ)=H(X)+H(Y|X)+H(Z|XY)
∵H(Z|XY)=H(Z|X)-I(Z;Y|X)
∴H(XYZ)=H(X)+H(Y|X)+H(Z|X)-I(Z;Y|X)
=H(XZ)+H(Y|X)-I(Z;Y|X)
2)H(XYZ)-H(XY)≤H(ZX)-H(X)
∵H(XYZ)-H(XY)
=H(X)+H(Y|X)+H(Z|XY)-H(X)-H(Y|X)
=H(Z|XY)
∵H(ZX)-H(X)=H(Z|X)
条件越多熵越小
H(Z|XY)≤H(Z|X)
得证
5.证明平均互信息量的极值性,即:I(X;Y)≤H(X),说明其意义及等式成立的条件。
意义:从集合Y的发生所获得的关于X的平均互信息量不会大于X本身的信息量H(X)
6、7、8三题汇总:









 本文详细探讨了通过掷骰子实验计算自信息量的方法,涉及'3和5同时出现'、'两个1同时出现'、'至少一个1'的事件,以及女孩身高和大学身份关联的信息熵。还解析了两个二元随机变量X和Y及其联合分布的条件熵和互信息量计算。
本文详细探讨了通过掷骰子实验计算自信息量的方法,涉及'3和5同时出现'、'两个1同时出现'、'至少一个1'的事件,以及女孩身高和大学身份关联的信息熵。还解析了两个二元随机变量X和Y及其联合分布的条件熵和互信息量计算。


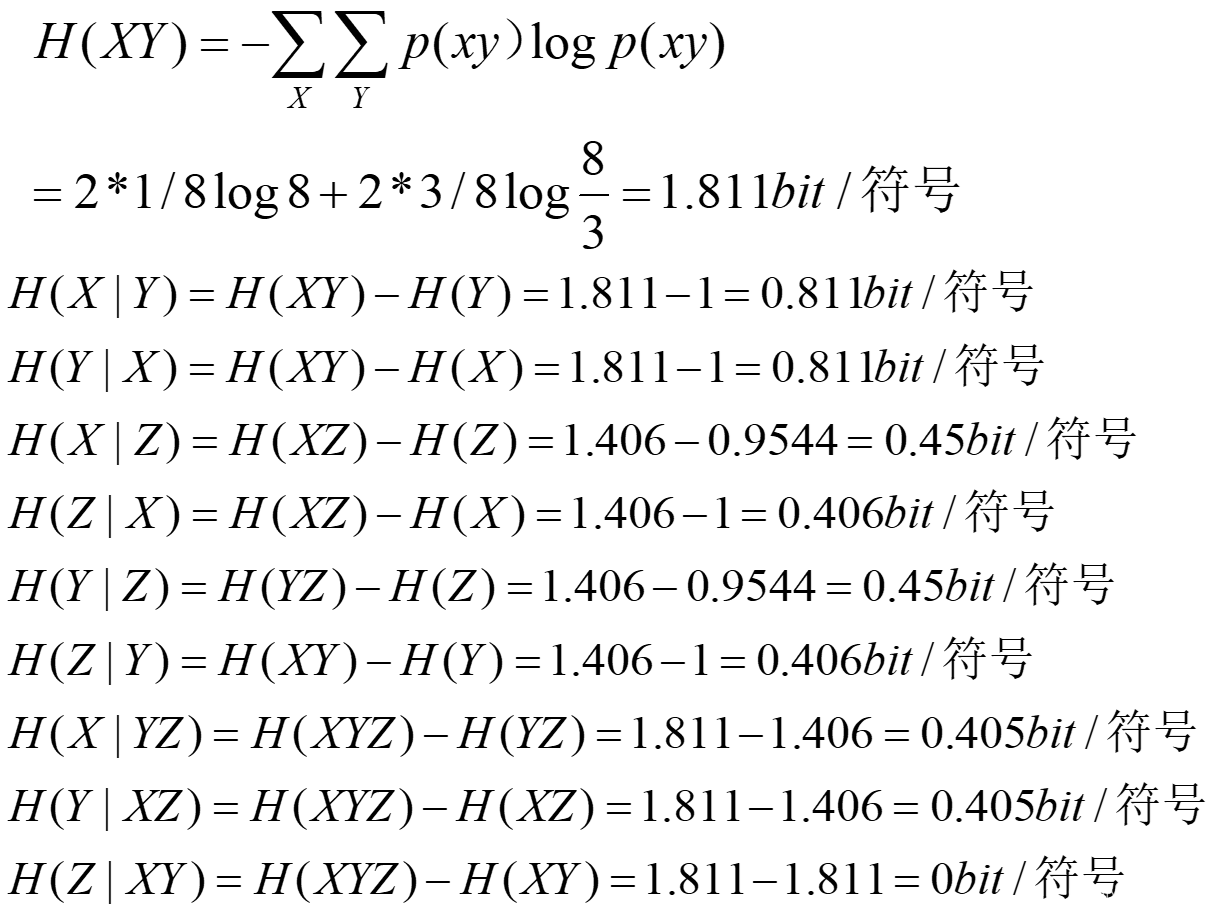

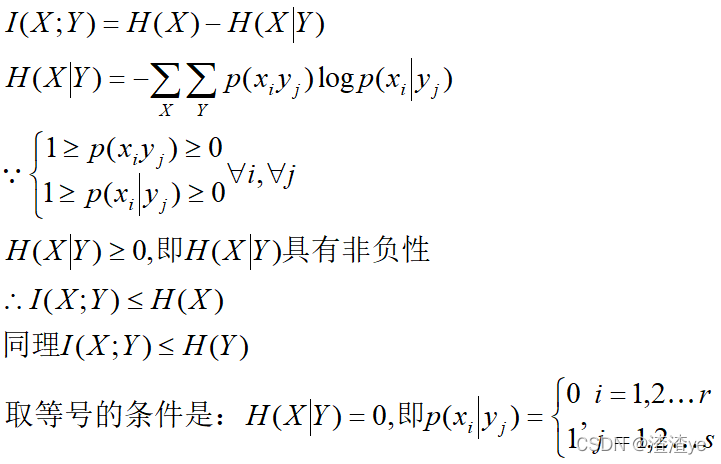

















 1694
1694

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










