番外—数学建模之LMDI模型附其Matlab代码样例

最新推荐文章于 2024-05-14 21:27:31 发布

1ce_cream_man

最新推荐文章于 2024-05-14 21:27:31 发布

阅读量3.9k

点赞数 10

分类专栏：番外—软件学习文章标签：数学建模 matlab 开发语言

本文链接：https://blog.csdn.net/yyyyyyyyyyjy/article/details/133391343

版权

番外—软件学习专栏收录该内容

5 篇文章

订阅专栏

本文介绍了LMDI模型的特点，其在能源和污染排放分析中的应用，以及如何通过Kaya模型进行数据处理和分解碳排放影响因素。示例展示了如何使用该模型计算各因素对碳排放的贡献，提出通过提高能源效率和非化石能源消费以实现双碳目标的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.LMDI模型介绍

LMDI方法具有以下特性：不包括不能解释的残差项，乘法分解的结果有加法特性，加法分解和乘法分解之间存在简单的对应关系，分部门效应加总与总效应保持一致等[1]。

二.模型适用范围

适用于能源强度变动和污染排放强度变动的因素分解分析。目前LMDI多数应用于碳排放、经济增长、技术融合度、行业就业人口、竞争力等领域。用简单的话来说，运用LMDI模型之后可以得到每个自变量对其因变量的贡献率。

三、模型使用方法和代码样例

例：2023华为杯研究生数学建模竞赛D题问题1中“分析对该区域碳排放量产生影响的各因素及其贡献”
①准备数据包括自变量和因变量，通常这些数据是一一系列时间点的观测值。
②对因变量和自变量取对数，这是LMDI的核心部分，通过取对数可以将分解转化为可加性的形式，方便分析。
③计算初始年和最终年的因变量总和，以及每个自变量的初始年和最终年总和。在对数化的数据上执行这些计算。
④计算因变量总和的增长率，通常是最终年总和与初始年总和的比率减去1。
⑤计算每个自变量对总增长率的贡献。这是通过计算自变量的比率变化（最终年与初始年的比率减去1）与其在总和中的权重来实现的。
⑥将增长率和每个自变量的贡献相乘，以获得LMDI分解的每个成分。
⑦分析LMDI分解的各个成分，以理解哪些因素对因变量的变化有更大的贡献。

基于Kaya模型[2]：二氧化碳排放量=人口×人均GDP×单位GDP能耗×单位能耗二氧化碳排放量
数学表达式如下：CO2=P * GDP/P * E/GDP * CO2/E
式中，CO2是二氧化碳排放量；P是人口；GDP/P是人均GDP；E/GDP是单位GDP能耗；CO2/E是单位能耗二氧化碳排放量。
将某东南沿海区域2010年至2020年间总碳排量、人口、GDP、能源消费量导入Excel表格中。图1：原数据
并基于Kaya公式对其进行数据预处理。
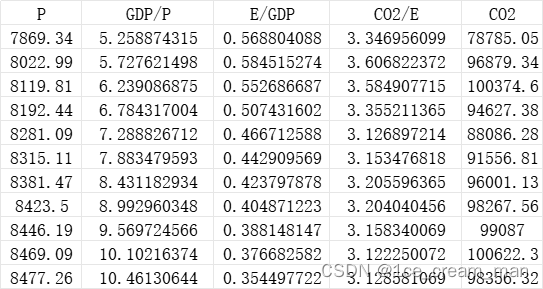
图2：预处理后的数据

% 导入你的数据，假设数据在一个名为'data.xlsx'的Excel文件中
data = xlsread('data.xlsx');

% 提取自变量和因变量
independent_vars = data(:, 1:4);
dependent_var = data(:, 5);

% 计算初始年和最终年的因变量总和
initial_year_total = sum(log(dependent_var(1)));
final_year_total = sum(log(dependent_var(end)));

% 计算每个自变量的初始年和最终年总和
initial_year_sum = sum(log(independent_vars(1, :)));
final_year_sum = sum(log(independent_vars(end, :)));

% 计算增长率
growth_rate = final_year_total - initial_year_total;

% 计算分解成分
component_changes = (log(independent_vars(end, :) / final_year_sum) - log(independent_vars(1, :) / initial_year_sum));
LMDI_components = growth_rate * component_changes;

% 输出结果
disp('LMDI Components:');
disp(LMDI_components);

运行结果如下：

LMDI Components:
    0.0122    0.1483   -0.1092   -0.0193

观察结果可知，在此区域中对总碳排量贡献相对较大的是人均GDP和单位GDP能耗，而其中单位GDP能耗和单位能耗二氧化碳排放量对总碳排量是负贡献。同时，单位GDP能耗也可以理解为区域能源利用效率，单位能耗二氧化碳排放量与非化石能源消费比重成反比，但此区域中非化石能源消费比重提高对碳排量做正贡献，因此若想在此区域实现碳达峰和碳中和的双碳目标，必须在提高非化石能源消费比重的同时提高能源利用效率并实现产业产品升级，以此进一步减少非化石能源的碳排放因子。