分类-3-生成学习-1-问题引入

在之前的学习方法中，我们的目的是求$p(y|x,\theta)$，即求y在x的条件下的概率。例如在逻辑回归中我们的模型是$h_\theta(x)=g(\theta^Tx)$，其输出结果就是预测样本属于某个类别的概率。对于二分类来说，它们的目的就是为了找到一个分割线（超平面）将样本划分为2类。当测试一个输入样本时，只需要看这个样本在分割线（超平面）的哪一侧。

回想贝叶斯公式：

$$p(y|x)=\frac{p(x|y)p(y)}{p(x)}$$
学过概率理论的人都知道条件概率的公式： $P(AB)=P(A)P(B|A)=P(B)P(A|B)$；即事件A和事件B同时发生的概率等于在发生A的条件下B发生的概率乘以A的概率。由条件概率公式推导出贝叶斯公式： $P(B|A)=\frac{P(A|B)P(B)}{P(A)}$；即,已知 $P(A|B)，P(A)$和 $P(B)$可以计算出 $P(B|A)$。
$P(A)$是 $A$的先验概率或边缘概率。之所以称为”先验”是因为它不考虑任何$B$方面的因素。
$P(A|B)$是已知 $B$发生后$A$的条件概率，也由于得自 $B$的取值而被称作$A$的后验概率。
$P(B|A)$是已知 $A$发生后$B$的条件概率，也由于得自 $A$的取值而被称作$B$的后验概率。
$P(B)$是 $B$的先验概率或边缘概率，也作标准化常量（normalized constant）。
假设$B$是由相互独立的事件组成的概率空间 $\{B_1,B_2，...B_n\}$。则 $P(A)$可以用全概率公式展开： $P(A)=P （A|B_1)P(B_1)+P（A|B_2)P(B_2)+..P（A|B_n)P(B_n)$。贝叶斯公式表示成： $P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+..P(A|B_n)P(B_n)}$；因此贝叶斯公式就可变为下面形式：
$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum_{i=1}^nP(A|B_i)P(B_i)}$$
$这里A就相当于我们的输入x，显然分母的值是固定不变的。因此在实际使用中我们并不需要考虑P(x)。$
因此可得我们的预测结果:

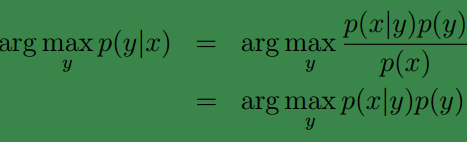
注： $argmax_yp(y|x)代表,输出使得p(y|x)最大的y$。

这种方法我们称为生成模型，而之前的一些方法称为辨别模型这篇博客较为详细地介绍了两个模型