问题
真实的训练数据总是存在各种各样的问题:
1、 比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余。
2、 拿到一个数学系的本科生期末考试成绩单,里面有三列,一列是对数学的兴趣程度,一列是复习时间,还有一列是考试成绩。我们知道要学好数学,需要有浓厚的兴趣,所以第二项与第一项强相关,第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢?
3、 拿到一个样本,特征非常多,而样例特别少,这样用回归去直接拟合非常困难,容易过度拟合。比如北京的房价:假设房子的特征是(大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数),搞了这么多特征,结果只有不到十个房子的样例。要拟合房子特征‐>房价的这么多特征,就会造成过度拟合。
4、 这个与第二个有点类似, 假设在 IR 中我们建立的文档‐词项矩阵中, 有两个词项为 “ learn”和“ study”,在传统的向量空间模型中,认为两者独立。然而从语义的角度来讲,两者是相似的,而且两者出现频率也类似,是不是可以合成为一个特征呢?
5、 在信号传输过程中,由于信道不是理想的,信道另一端收到的信号会有噪音扰动,那么怎么滤去这些噪音呢?
下面探讨一种称作主成分分析( PCA)的方法来解决部分上述问题。 PCA 的思想是将 n维特征映射到 k 维上 (k<n) ,这 k 维是全新的正交特征。这 k 维特征称为主元,是重新构造出来的 k 维特征,而不是简单地从 n 维特征中去除其余 n‐k 维特征。
PCA 计算过程
首先介绍 PCA 的计算过程:
假设我们得到的 2 维数据如下:
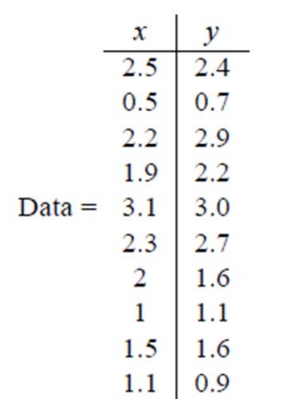
行代表了样例,列代表特征,这里有 10 个样例,每个样例两个特征。可以这样认为,有 10 篇文档,x 是 10 篇文档中“learn”出现的 TF‐IDF,y 是 10 篇文档中“study”出现的TF‐IDF。也可以认为有 10 辆汽车,x 是千米/小时的速度,y 是英里/小时的速度,等等。
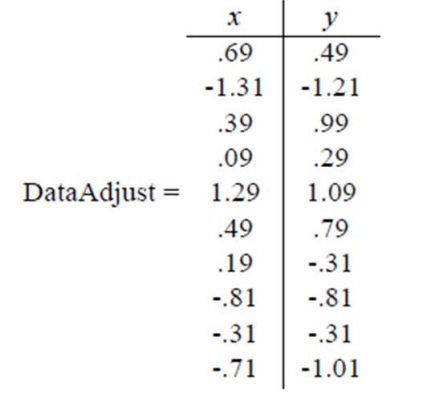
第一步分别求 x 和 y 的平均值,然后对于所有的样例,都减去对应的均值。这里 x 的均值是 1.81,y 的均值是 1.91,那么一个样例减去均值后即为(0.69,0.49),得到
第二步,求特征协方差矩阵:
如果数据是 3 维,那么协方差矩阵是
这里只有 x 和 y,求解得:
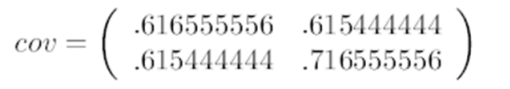
对角线上分别是 x 和 y 的方差,非对角线上是x和y 的协方差。协方差大于 0 表示 x 和 y 若有一个增,另一个也增;小于 0 表示一个增,一个减;协方差为 0 时,两者独立。协方差绝对值越大,两者对彼此的影响越大,反之越小。
第三步,求协方差的特征值和特征向量,得到:
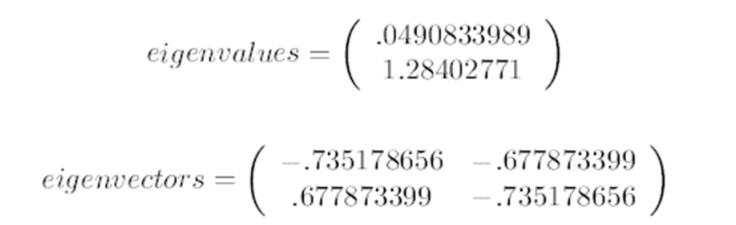
上面是两个特征值,下面是对应的特征向量,特征值
0.0490833989
对应特征向量为
(−0.735178656,0.677873399)T
,这里的特征向量都归一化为单位向量。
第四步,将特征值按照从大到小的顺序排序,选择其中最大的
k
然后将其对应的
这里特征值只有两个,我们选择其中最大的那个,这里是 1.28402771, 对应的特征向量 是(−0.677873399,−0.735178656)T
第五步,将样本点投影到选取的特征向量上。假设样例数为 m,特征数为 n,减去均值后的样本矩阵为 DataAdjust(m*n),协方差矩阵是 n*n,选取的 k 个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据 FinalData 为
这里是
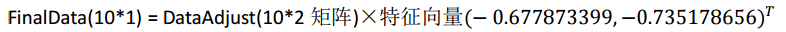
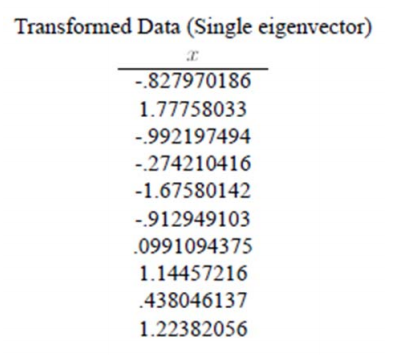
得到结果是
这样,就将原始样例的 n 维特征变成了 k 维,这 k 维就是原始特征在 k 维上的投影。
上面的数据可以认为是 learn 和 study 特征融合为一个新的特征叫做 LS 特征,该特征基本上代表了这两个特征。
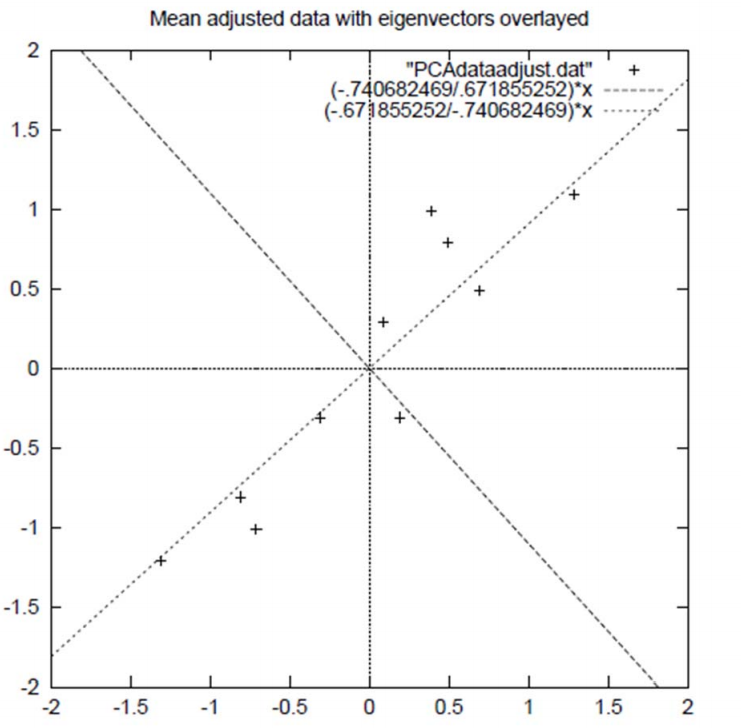
上述过程有个图描述:
正号表示预处理后的样本点,斜着的两条线就分别是正交的特征向量(由于协方差矩阵是对称的,因此其特征向量正交),最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。
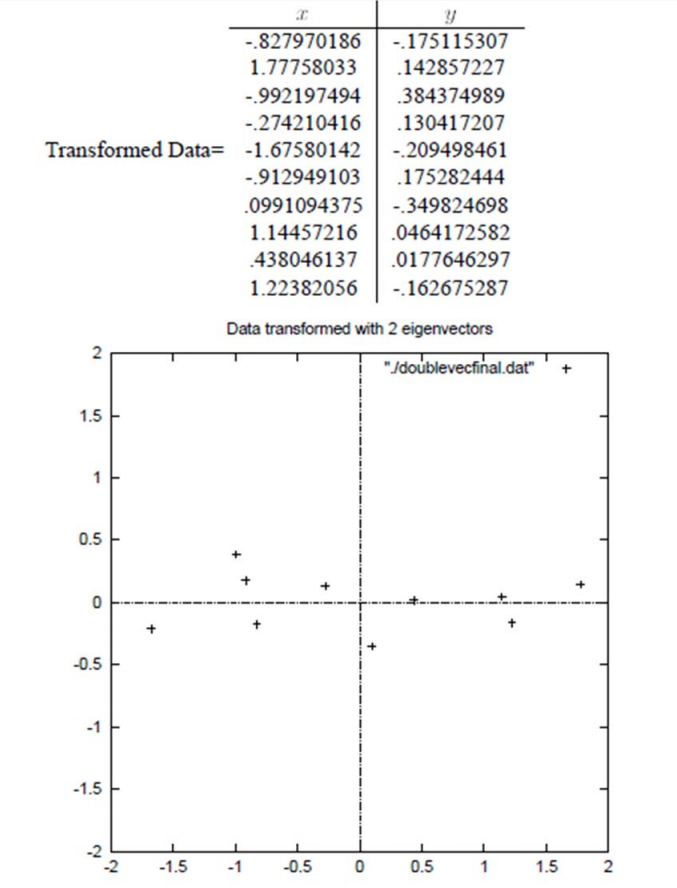
如果取的 k=2,那么结果是
这就是经过 PCA 处理后的样本数据,水平轴(上面举例为 LS 特征)基本上可以代表全部样本点。整个过程看起来就像将坐标系做了旋转,当然二维可以图形化表示,高维就不行了。上面的如果 k=1,那么只会留下这里的水平轴,轴上是所有点在该轴的投影。
这样 PCA 的过程基本结束。在第一步减均值之后,其实应该还有一步对特征做方差归一化。比如一个特征是汽车速度(0 到 100),一个是汽车的座位数(2 到 6),显然第二个的方差比第一个小。因此,如果样本特征中存在这种情况,那么在第一步之后,求每个特征的
标准差σ,然后对每个样例在该特征下的数据除以σ。
归纳一下,使用我们之前熟悉的表示方法,在求协方差之前的步骤是:
其中 x(i) 是样例,共m个,每个样例n个特征,也就是说 x(i) 是n维向量。 x(i)j 是第i个样例的第j个特征。 μ 是样例均值。 σj 是第j个特征的标准差。
整个 PCA 过程貌似及其简单,就是求协方差的特征值和特征向量,然后做数据转换。但是有没有觉得很神奇,为什么求协方差的特征向量就是最理想的 k 维向量?其背后隐藏的意义是什么?整个 PCA 的意义是什么?
请看下一篇










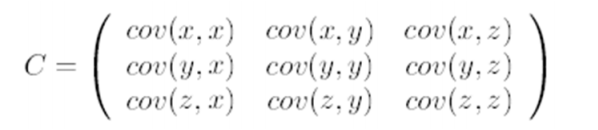
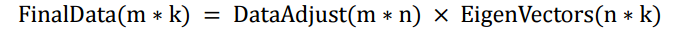
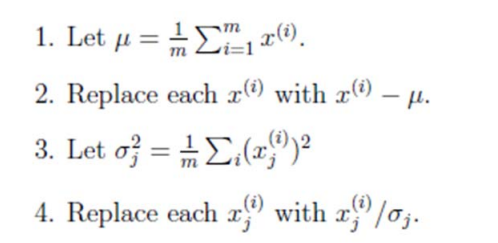














 3496
3496











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








