PCA和PCOA

其实不论是PCoA还是PCA图均是用散点图来展示结果PCoA和PCA的结果，PCoA和PCA准确来讲是数据降维分析方法。
顺便值此佳节，祝福各位和“科研”都能够拥有幸福时光和美好结局。

什么是PCA和PCoA

主成分分析（Principal components analysis，PCA）是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分（Principal Components）。具体地，主成分可以看做一个线性方程，其包含一系列线性系数来指示投影方向（如图）。PCA对原始数据的正则化或预处理敏感（相对缩放）。PCA是最简单的以特征量分析多元统计分布的方法。通常情况下，这种运算可以被看作是揭露数据的内部结构，从而更好的解释数据的变量的方法。

 

PCA示意图

主坐标分析（Principal Coordinates Analysis，PCoA），即经典多维标度（Classical multidimensional scaling），用于研究数据间的相似性。PCoA与PCA都是降低数据维度的方法，但是差异在在于PCA是基于原始矩阵，而PCoA是基于通过原始矩阵计算出的距离矩阵。因此，PCA是尽力保留数据中的变异让点的位置不改动，而PCoA是尽力保证原本的距离关系不发生改变，也就是使得原始数据间点的距离与投影中即结果中各点之间的距离尽可能相关（如图）。

 

PCoA示意图

如何进行PCA和PCoA分析

R中有很多包都提供了PCA和PCoA,比如常用的ade4包。本文将基于该包进行PCA和PCoA的分析，数据是自带的deug，该数据提供了104个学生9门课程的成绩（见截图）和综合评定。综合评定有以下几个等级：A+,A,B,B-,C-,D。
让我们通过PCA和PCoA来看一看这样的综合评定是否合理，是否确实依据这9门课把这104个学生合理分配到不同组（每个等级一个组）。

 

deug的9门课

（1）PCA分析及作图
前文已经介绍了PCA是基于原始数据，所以直接进行PCA分析即可。由于前面已经介绍过散点图的绘制方法，这里不再细讲，PCA分析完毕后我们直接作图展示结果。

 

library(ade4)
library(ggplot2)
library(RColorBrewer)
data(deug)

#PCA分析
pca<- dudi.pca(deug$tab, scal = FALSE, center = deug$cent, scan = FALSE)

#坐标轴解释量（前两轴）
pca_eig <- (pca$eig)[1:2] / sum(pca$eig)

#提取样本点坐标（前两轴）
sample_site <- data.frame({pca$li})[1:2]
sample_site$names <- rownames(sample_site)
names(sample_site)[1:2] <- c('PCA1', 'PCA2')

#以最终成绩作为分组
sample_site$level<-factor(deug$result,levels=c('A+','A','B','B-','C-','D'))

library(ggplot2)

pca_plot <- ggplot(sample_site, aes(PCA1, PCA2,color=level)) +
  theme_classic()+#去掉背景框
  geom_vline(xintercept = 0, color = 'gray', size = 0.4) + 
  geom_hline(yintercept = 0, color = 'gray', size = 0.4) +
  geom_point(size = 1.5)+  #可在这里修改点的透明度、大小
  scale_color_manual(values = brewer.pal(6,"Set2")) + #可在这里修改点的颜色
  theme(panel.grid = element_line(color = 'gray', linetype = 2, size = 0.1), 
        panel.background = element_rect(color = 'black', fill = 'transparent'), 
        legend.title=element_blank()
  )+
  labs(x = paste('PCA1: ', round(100 * pca_eig[1], 2), '%'), y = paste('PCA2: ', round(100 * pca_eig[2], 2), '%')) 

pca_plot

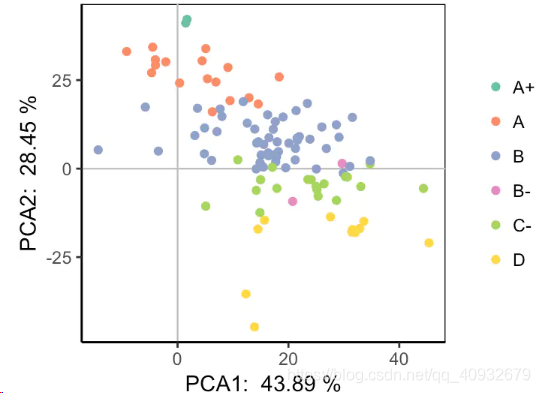
整体看起来还不错，就是B-和C-的学生似乎难以区分。

（2）PCoA分析及作图

 

library(ade4)
library(ggplot2)
library(RColorBrewer)
library(vegan)#用于计算距离
data(deug)
tab<-deug$tab
tab.dist<-vegdist(tab,method='euclidean')#基于euclidean距离
pcoa<- dudi.pco(tab.dist, scan = FALSE,nf=3)

#坐标轴解释量（前两轴）
pcoa_eig <- (pcoa$eig)[1:2] / sum(pcoa$eig)

#提取样本点坐标（前两轴）
sample_site <- data.frame({pcoa$li})[1:2]
sample_site$names <- rownames(sample_site)
names(sample_site)[1:2] <- c('PCoA1', 'PCoA2')

#以最终成绩作为分组
sample_site$level<-factor(deug$result,levels=c('A+','A','B','B-','C-','D'))

library(ggplot2)

pcoa_plot <- ggplot(sample_site, aes(PCoA1, PCoA2,color=level)) +
  theme_classic()+#去掉背景框
  geom_vline(xintercept = 0, color = 'gray', size = 0.4) + 
  geom_hline(yintercept = 0, color = 'gray', size = 0.4) +
  geom_point(size = 1.5)+  #可在这里修改点的透明度、大小
  scale_color_manual(values = brewer.pal(6,"Set2")) + #可在这里修改点的颜色
  theme(panel.grid = element_line(color = 'gray', linetype = 2, size = 0.1), 
        panel.background = element_rect(color = 'black', fill = 'transparent'), 
        legend.title=element_blank()
  )+
  labs(x = paste('PCoA1: ', round(100 * pcoa_eig[1], 2), '%'), y = paste('PCoA2: ', round(100 * pcoa_eig[2], 2), '%')) 

pcoa_plot

有时候PCA和PCoA的结果差不多，有时候某种方法能够把样本有效分开而另一种可能效果不佳，这些都要看样本数据的特性。
因为没有现成可供分享的微生物组数据，所以用了这个成绩的数据集。通常来说在微生物组的研究中，我们会根据物种丰度的文件对数据进行PCA或者PCoA分析，也是我们所说的beta-diveristy分析，根据PCA或者PCoA的结果看疾病组和对照组能否分开，以了解微生物组的总体变化情况。