转载http://www.cnblogs.com/jerrylead/archive/2011/04/19/2021071.html
问题:
1、上节提到的PCA是一种数据降维的方法,但是只对符合高斯分布的样本点比较有效,那么对于其他分布的样本,有没有主元分解的方法呢?
2、经典的鸡尾酒宴会问题(cocktail party problem)。假设在party中有n个人,他们可以同时说话,我们也在房间中一些角落里共放置了n个声音接收器(Microphone)用来记录声音。宴会过后,我们从n个麦克风中得到了一组数据
{x(i)(x(i)1,...,x(i)n);i=1,...,m}
,
i
表示采样的时间顺序,也就是说共得到了
将第二个问题细化一下,有n个信号源 s(s1,...sn)T,s∈R ,每一维都是一个人的声音信号,每个人发出的声音信号独立。A是一个未知的混合矩阵(mixing matrix),用来组合叠加信号s,那么
x是输入信号混合后的结果,这里的x不是一个向量,是一个矩阵,每个
x(i)
对应一个麦克风中的混合信号。其中每个列向量是
x(i),x(i)=As(i)
表示成图就是
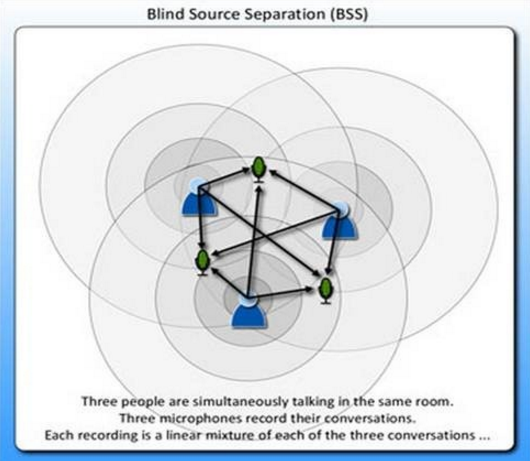
这张图来自
x(i) 的每个分量都由 s(i) 的分量线性表示。A和s都是未知的,x是已知的,我们要想办法根据x来推出s。这个过程也称作为盲信号分离。
令 W=A−1 ,那么 s(i)=A(−1)x(i)=Wx(i)
将
W
表示成
其中
ICA的不确定性(ICA ambiguities)
由于w和s都不确定,那么在没有先验知识的情况下,无法同时确定这两个相关参数。比如上面的公式s=wx。当w扩大两倍时,s只需要同时扩大两倍即可,等式仍然满足,因此无法得到唯一的s。同时如果将人的编号打乱,变成另外一个顺序,如上图的蓝色节点的编号变为3,2,1,那么只需要调换A的列向量顺序即可,因此也无法单独确定s。这两种情况称为原信号不确定。
还有一种ICA不适用的情况,那就是信号不能是高斯分布的。假设只有两个人发出的声音信号符合多值正态分布,
s∼N(0,1)
,
I
是2*2的单位矩阵,s的概率密度函数就不用说了吧,以均值0为中心,投影面是椭圆的山峰状(参见多值高斯分布)。因为
令R是正交阵 (RRT=RTR=I),A′=AR .如果将A替换成A’。那么 x′=A′s .s分布没变,因此x’仍然是均值为0,协方差 E[x′(x′)T]=E[A′ssT(A′)T]=E[ARssT(AR)T]=ARRTAT=AAT
因此,不管混合矩阵是A还是A’,x的分布情况是一样的,那么就无法确定混合矩阵,也就无法确定原信号。
密度函数和线性变换
在讨论ICA具体算法之前,我们先来回顾一下概率和线性代数里的知识。
假设我们的随机变量s有概率密度函数
ps(s)
(连续值是概率密度函数,离散值是概率)。为了简单,我们再假设s是实数,还有一个随机变量
x=AS
,A和x都是实数。令
px
是x的概率密度,那么怎么求
px
?
令
W=A−1
,首先将式子变换成
s=Wx
,然后得到
px(x)=ps
,求解完毕。可惜这种方法是错误的。比如s符合均匀分布的话(
s∼Uniform[0,1]
),那么s的概率密度是
ps(s)=1{0≤s≤1}
,现在令A=2,即x=2s,也就是说x在[0,2]上均匀分布,可知
px(x)=0.5
。然而,前面的推导会得到
px(x)=ps(0.5s)=1
.正确的公式应该是
推导方法
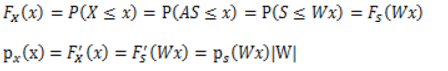
更一般地,如果s是向量,A可逆的方阵,那么上式子仍然成立。
ICA算法
ICA算法归功于Bell和Sejnowski,这里使用最大似然估计来解释算法,原始的论文中使用的是一个复杂的方法Infomax principal。
我们假定每个
si
有概率密度
ps
,那么给定时刻原信号的联合分布就是
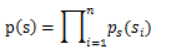
这个公式代表一个假设前提:每个人发出的声音信号各自独立。有了p(s),我们可以求得p(x)
左边是每个采样信号x(n维向量)的概率,右边是每个原信号概率的乘积的|W|倍。
前面提到过,如果没有先验知识,我们无法求得W和s。因此我们需要知道
ps(si)
,我们打算选取一个概率密度函数赋给s,但是我们不能选取高斯分布的密度函数。在概率论里我们知道密度函数p(x)由累计分布函数(cdf)F(x)求导得到。F(x)要满足两个性质是:单调递增和在[0,1]。我们发现sigmoid函数很适合,定义域负无穷到正无穷,值域0到1,缓慢递增。我们假定s的累积分布函数符合sigmoid函数
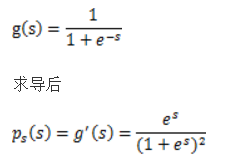
这就是s的密度函数。这里s是实数。
如果我们预先知道s的分布函数,那就不用假设了,但是在缺失的情况下,sigmoid函数能够在大多数问题上取得不错的效果。由于上式中 ps(s) 是个对称函数,因此E[s]=0(s的均值为0),那么E[x]=E[As]=0,x的均值也是0。
知道了
ps(s)
,就剩下W了。给定采样后的训练样本
{x(i)(x(i)1,...,x(i)n);i=1,...,m}
,样本对数似然估计如下:
使用前面得到的x的概率密度函数,得
大括号里面是 p(x(i)) .
接下来就是对W求导了,这里牵涉一个问题是对行列式|W|进行求导的方法,属于矩阵微积分。这里先给出结果,在文章最后再给出推导公式。
最终得到的求导后公式如下,
logg′(s)
的导数为
1−2g(s)
可以自己验证):
其中
α
是梯度上升速率,人为指定。
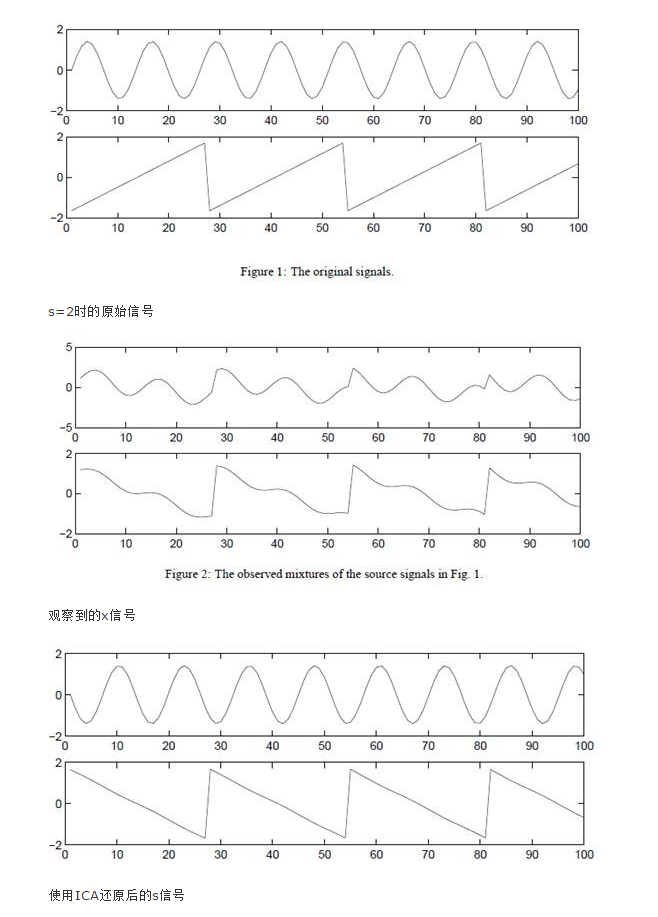
当迭代求出W后,便可得到
s(i)=Wx(i)
来还原出原始信号。
注意:我们计算最大似然估计时,假设
x(i)与x(j)
之间是独立的,然而对于语音信号或者其他具有时间连续依赖特性(比如温度)上,这个假设不能成立。但是在数据足够多时,假设独立对效果影响不大,同时如果事先打乱样例,并运行随机梯度上升算法,那么能够加快收敛速度。
回顾一下鸡尾酒宴会问题,s是人发出的信号,是连续值,不同时间点的s不同,每个人发出的信号之间独立s的累计概率分布函数是sigmoid函数,但是所有人发出声音信号都符合这个分布。A(W的逆阵)代表了s相对于x的位置变化,x是s和A变化后的结果。










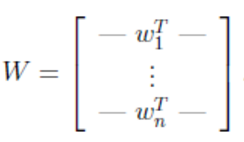
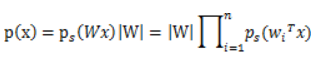
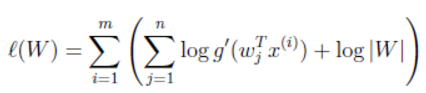
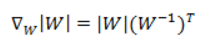
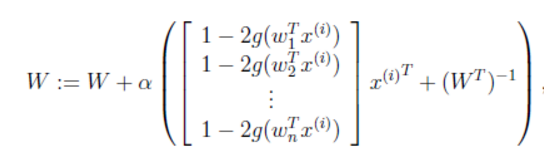















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








