Symbolic regression in materials science

Introduction

作者先简述了目前前沿方法 基于遗传编程的符号回归算法（genetic programming-based symbolic regression (GPSR)） 和最近符号回归中的先进技术。之后，团队论述了符号回归的工业应用和在材料科学的潜在应用。作者展示了两个GPSR的使用案例：

1. 建立转化动力学规律，并给出学习方案，发现著名的Johnson-Mehl-Avrami-Kolmogorov(JMAK)形式
2. 学习了钙钛矿(perovskite)LaNiO3中位移倾斜转变(displacive tilt transition)的朗道自由能泛函形式(Landau free energy functional form)

最后，作者建议材料科学家考虑将符号回归技术作为从数据中学习的其他基于机器学习的回归模型的替代方案。

Motivation

A. 材料科学中的大数据时代

先用日心学说的起源和定律发展作为例子，说明了这个过程中的数据获取(Brahe)，数据分析(Kepler)，和第一原理的推导(牛顿)大概是什么样子的。

而材料科学随着计算机技术、建模理论、实验仪器等的发展也进入了材料的大数据时代。材料信息的数据集可以从先进的表征技术、组合实验、高通量第一原理模拟、文献挖掘和其他技术中获得，日渐减少人工，并且所有这些数据使我们有机会为以前缺乏现象学行为的系统构建新的规律。

受MGI启发，材料界正在共同努力，使数字材料数据向他人开放。多个材料数据库如 Material Projects，OQMD，AFLOWLIB,OMDB,AiiDA,Citrination和NOMAD公开了数百万条材料数据点。这为发现材料加工-结构-性能-性能关系的支配规律的下一步“自动化开普勒”铺平了道路，这可能促进材料的发现、开发和技术创新。

由于材料科学和工程的基本研究目标之一是在特定的约束条件下提供具有最佳性能的新材料，因此了解如何以及哪些特性控制功能是至关重要的，换句话说，哪些自由度(或参数)和它们对应的内在关系(或依赖关系)与材料的特性应该被优化。但是材料科学的多尺度特性，从原子尺度的晶体结构到复杂的中尺度域结构（mesoscale domain structures）和体力学性能(bulk mechanical properties)，或者从飞秒激光探针(femotosecond laser probes)到长达一小时的再结晶反应，这使得研究不同材料族的许多层次关系具有特别的挑战性。给定这样一个高维的参数空间(例如化学成分、晶体结构、外部条件等)，材料科学家通常探索一个有限的子空间，包含所有控制材料属性和性能的因素。此外，已有数据集通常分布稀疏。尽管大型材料数据库的建立在一定程度上缓解了数据有限的问题，但迫切需要一个健壮的数据处理协议，以帮助识别材料科学中的支配规律，并提供设计材料和合成/加工程序。

B. 机器学习方法的另一种选择

许多新兴的材料信息学领域关注上述挑战。机器学习模型是目前发现这些定律的可供选择的工具，在预测材料性能上有着可观的性能表现，但典型的参数化机器学习模型不利于实现“自动化牛顿”的最终目标。

ML模型虽然能做预测，但是其描述冗长啰嗦（比如深度学习模型有着数千级的参数），或者有着数理限制（假定目标变量为输入特征的线性组合），类似的黑箱模型在现代材料科学研究中非常流行。然而，这些模型的可解释性一直是个问题。尽管有大量关于数据可视化和模型理解的工作来解决这些问题，但这些主题将超出此视角的范围(参见参考文献18的回顾)。

这篇文章中，作者聚焦于符号回归方法。符号回归同时搜索给定问题的函数和参数集的最佳形式，当数据结构/分布的先验知识很少时，它是一种强大的回归技术。

fig1展示了机器学习和符号回归在不同研究领域的相对热度。

1. related publications：可以看到在所有与机器学习或符号回归相关的出版物中，超过50%的贡献来自计算机科学研究界，而多学科工程是第二。社会科学和自然科学各占出版物总数的不到20%。这两种技术在材料科学研究中并不流行，相对于其他研究领域，它们的贡献几乎可以忽略不计。值得注意的是在社会学科中符号回归比机器学习更加流行，其中的一个可能原因是，社会科学问题通常不像许多物理科学中那样具有(已知的)物理驱动的控制方程，例如牛顿运动方程、薛定谔方程等可以被正式书写。符号回归有潜力从社会科学数据集(如问卷调查结果、行为模式等)中找到合适的函数形式。
2. ln(publications)：报告了以下机器学习、机器学习在材料科学中的应用和符号回归这三个研究领域的发表数量(以自然对数尺度)的趋势，这三个领域都呈指数级的发展率，然而，与机器学习相关的出版物数量比其他两个要多出几个数量级。由于基数太小，这里没有显示符号回归在材料科学中的应用趋势。尽管如此，它也揭示了一个以前不被重视的潜在研究领域。对于材料科学问题，人们还经常遇到许多变量之间的未知关系的问题。于是，符号回归提供了一个机会，帮助从这些变量中推导出结构-属性关系。

II. 符号回归和目前先进方法

A. Genetic programming-based symbolic regression (GPSR)

传统回归中，模型的优化参数为算法的起始点。例如，线性回归模型是基于因变量和回归变量之间的关系是线性的假设；人工神经网络依赖预定义的网络结构如神经元和激活函数。然而，在符号回归中，对函数的特定形式不需要这样的先验假设。相反，它提供一个包含候选函数构建块的数学表达式空间，例如，数学运算符、状态变量、常数、解析函数，然后符号回归在这些基本构建块所跨越的空间中搜索，以找到最合适的解。也就是说符号回归优化了模型结构和模型参数。因为不需要预定义的函数形式，所以符号回归中的优化算法也和传统分析/数值优化方法不同。

1. 与GA中使用二进制数字字符串表示染色体不同，GP中的解表示为带有节点和终端的树结构染色体。

fig2展示了数学函数1 + exp(−x1)的一个染色体例子。该树由一组具有数学运算的内部节点和具有变量和常量的终端节点组成。可用深度优先搜索来遍历该树获得每个独立解的最终数理表达。该染色体树的结构并非一定要是二元的，其结构取决于数学运算符的参数个数。GP的用户可以包含适合他们的目标问题的各种功能。算法将根据指定的用户设置生成大量的树，并在整个GP过程中进行评估迭代。每个树代表着该问题的可能解，并从最初的数学构建模块生成新树。

其中a，b两棵树作为亲本，然后交叉运算从父树(b)中随机取一个子树，用父树(b)中的子树替换父树(a)中的另一随机子树。它们从交叉运算中得到的一个可能后代如c所示。变异操作只接受一个父结构，并将子树随机替换为另一个随机生成的结构。a从变异运算中得到的一个可能后代为d。变异操作为系统增加了随机性，因此引入新变量(例如新常数和新特征)的突变机会是有限的，并避免陷入局部极小值(local minima)是很重要的。

第三种遗传操作为繁殖，它复制所选程序并直接插入下一代中。该操作保证了当前一代某些特征在下一代中保留，在一定程度上保护了两代之间的相似性，每个遗传操作的详细定义和实现可能因情况而异，但主要特征应该与我们在这里描述的相似。

每次遗传操作后新产生的树会加入下一代中，直到新产生树的个数达到某一确切预设的值。之后新一代再进行拟合预估和自然选择过程，直到该拟合值达到特定标准或者该代树的数量达到最大值。在GP终止后，存活个体有望高度进化以适应问题依赖的选择规则。更全面的GP描述可以在Koza的原始论文中找到。

2. fig3说明了利用遗传规划得到符号回归问题解的过程

该过程从一组随机生成的初始终端节点(变量、常数)和函数开始，形成具有不同大小和结构的独立树(如fig2所示)，这些基本构建块来自用户定义的输入集。由于随机过程，这种初始种群通常具有多种多样的树形结构，这有助于进一步探索变量空间，并降低陷入局部极小值的潜在风险。一旦个体数量达到用户定义的种群大小，初始化过程就会终止，这时自然选择过程就会开始发挥作用。然后，通过将初始总体中每个单独解的函数输出与数据集中的真实值进行比较，来评估它们的“拟合度”。该拟合值描述了程序在解决该问题的表现如何。常用误差矩阵包含MSE和RMSE。然后GP通过对个体进行随机的遗传操作，如交叉和突变，来进化当前的一代。根据适合度分数，当代的一个或多个个体被选为亲本进行下一代遗传。

B. Advances in symbolic regression

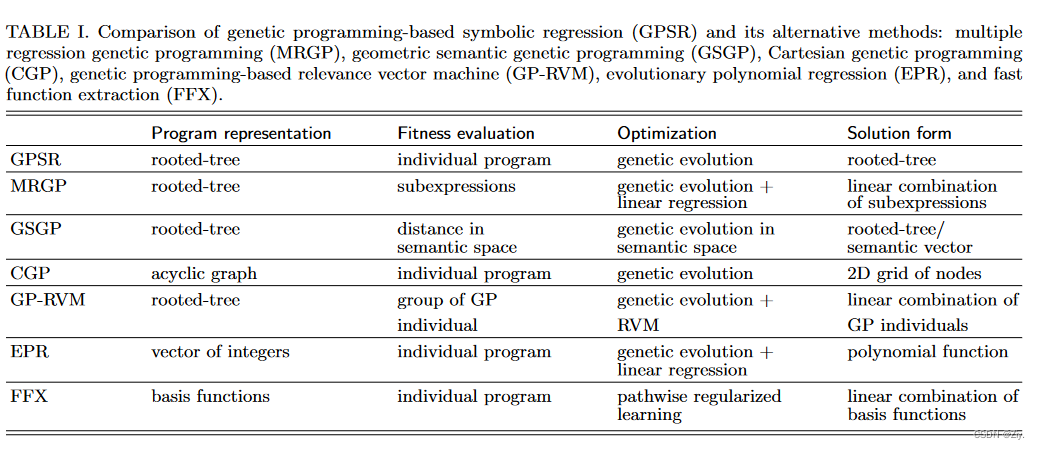
多元回归遗传规划(Multiple regression genetic programming (MRGP)) 通过对解函数的子表达式执行多重回归来改进程序的评估过程。而不是评估每个单独的解作为一个整体的适应度，MRGP解耦其数学表达式树到子树。基于这些子树结构的最佳线性组合来评估解的适应度。最小角度回归(A least angle regression (LARS)) 用来解决这里的线性回归问题。这样的适应性评估方案更强调寻找好的组件，即使它可能只是一个部分的解决方案。

几何语义遗传规划(Geometric semantic genetic programming (GSGP)) 它评估计算机程序的语义性能，而不是像传统的GPSR那样评估语法性能。

笛卡尔遗传规划(Cartesian genetic programming (CGP)) 中一个计算机程序被表示为一个有向无环图，它可以被可视化为一个二维节点网格。每个节点都拥有一组基因，这些基因决定了节点执行的输入输出和数学功能;计算机程序的整套基因组成了它的基因型。对基因型的解码导致显型，即计算机程序的功能形式。基因型-表型映射是CGP的一个独特特征，使其更接近真实的自然过程。

基于遗传规划的相关向量机(genetic programming-based relevance vector machine,GP-RVM)

进化多项式回归(evolutionary polynomial regression,EPR)

快速函数提取(fast function extraction (FFX))

III. APPLICATIONS OF SYMBOLIC REGRESSION

A. Industrial applications

有学者使用GPSR确定在多种优化条件下燃气涡轮发动机的控制方程、将GPSR用于解释复杂数值模型或者系统、利用具有稀疏约束的GPSR从实验传热测量中识别相关方程(作者预测的相关性比图形和数字模型的误差百分比更低，尽管公式比传统方法更复杂)

fig4为Pareto front论文说明了由方程中操作的数量和类型定义的模型复杂性与预测误差中的归一化方差(variance accounted for,VAF)之间的权衡。这些研究人员通过从非线性常微分方程和现实系统中找到合成数据的紧凑动态方程，证明了他们的改进提高了标准GPSR的性能

B. Opportunities in materials science

材料学中有很多潜在领域都可以用GPSR以同样的方式来发现其他的定律，非线性系统在材料学中通常是冗余的。在结构、成分和其他外部扰动的响应下，材料性能的变化往往是接近相变或大刺激的非线性变化。

C. Use cases in materials science

1. Discovering the Johnson-Mehl-AvramiKolmogorov equation

作者在gplearn中使用GPSR来预测转变分数y和时间t，GPSR中使用的超参数如下：

tableii中，GPSR中用到的超参数列表用于学习Avrami方程。采用网格搜索的方法，从最上面的三个参数集中寻找最优超参数。

fig5中，作者将铜重结晶实验在135°C，113°C和102°C的数据作为输入，并在回归之前缩放时间变量。由于实验数据在每个温度下只有几个点(小于10)，我们也从插值线中取数据点，对插值数据进行符号回归进行比较。该实验生成了一组理想数据集，其中y值可以用公式$1-exp(-0.6t^2)$计算得出。给定Avrami函数形式，每组数据集中最优的k和n通过使用Scipy数值拟合得出，理想情况下，GPSR应该能够为所有数据集恢复正确的函数形式以及k和n常数。

在fig5(e)中，模型预测的函数形式为线性，严重偏离了原始数据，结果较差可能是由于原始数据的斜率相对较小，可用数据点数量不足。考虑到模型的性能和复杂性，作者认为线性关系由于形式简单而为最终呈现结果。

在fig5(f)中，作者将插值数据作为输入，发现由GPSR演化而来的函数更加符合Avrami方程。也由此发现，充足的训练数据课题提高GPSR的模型性能，这一点对于其他数据驱动方法也同样适用。

tableiii中，Gplearn能够成功揭示大部分情况下时间t和转变分数y的关系。如果输入是理想的数据，gplearn进化的Avarmi函数形式和常量几近完美。在大多数情况下，t的指数函数形式和多项式函数都可以恢复。错误的一个来源是在函数集中缺少幂函数，这是故意省略的，因为变量的非整数幂在这里不能正确表示。相反，多项式函数被用作近似。由于数学函数的选择有限，GP产生的结果在语义上非常接近，但显示出不同的语法。

作者发现通过转换(或简化)数学表达式，也可以提高GPSR的性能。 在tableiii的最后一列中，作者对比了直接训练$y\backsim t$和$(1-y)\backsim t$的关系，后者目标值$1-y$为未转化铜的百分比。 因为作者已经为模型执行了减法，转换后的函数显示性能有所改进，GPSR不仅成功地恢复了方程的指数形式，而且找到了更接近数值拟合值的常数。

函数$e^x$与$1+x$为等价无穷小，即$\underset{x\to 0}{\lim }{e}^x\backsim 1+x$。在此例子中，当$\theta$(其理想形式为$-k{t}^n$)变得更负时，指数项$-\exp (\theta )$很快达到零。因此，等价无穷小关系成立，函数的预测形式等价于Avrami表达式中出现的期望形式。类似于此例子，专业材料研究者在对得到的模型进行最终解释时能对GPSR结果进行仔细分析。

在实际的应用程序中，实际的函数形式是未知的，GPSR结果的确切语法可能并不重要。在很多情况下，GPSR可能会产生语义上相似/等效的函数，但它们的语法不同，即不同的函数形式。考虑到模型的准确性和复杂性之间的权衡，在某些情况下，找到一个简单的近似解而不是使用多个变量之间严格但复杂的关系可能是一个优点。

2. Learning Landau free energy expansion(学习朗道自由能膨胀)

作者在该部分研究的模型为钙钛矿$LaNi{O}_3$立方到六方结构相变的朗道自由能，此处系统的自由能G按一个阶参数θ的幂展开

$$G\left(\theta ,T\right)=G_0\left(T\right)+\kappa \left(T-T_C\right){\theta }^2+\lambda {\theta }^4$$
其中温度T和阶参数$\theta$为输入，自由能变化$G(\theta ,T)-G_0(T)$为输出.