贝叶斯决策论
核心:实质是将期望风险降到最低。这等价于将后验概率最大化。 为什么??
解释:
有标记Y={C1,C2.....Cn},样本x可能被错误标记为Ci。则根据后验概率可得到P(Ci|x) (公式的意思是:样本x被标记为Ci的概率。)则总的条件风险为 R(Ci|x)= (是标记错误的损失函数)。所以得到优化任务:最小化条件风险R(Ci|x)。。。
这里=
推荐:
R(Ci|x)=
=arg min
=arg min
=arg min (1-P(Ci=j | x))
=arg max P(Ci=j | x))
这里就转化过来了,这就是贝叶斯决策论。。
贝叶斯分类器
求得arg max P(Ci=j | x)),下面怎么求这个呢??
利用贝叶斯公式得到
因为样本x 是固定的,所以只需求P(x|C)P(C)即可
利用极大似然发求max P(x|C)P(C)
极大似然法:
把发生概率最高的参数作为真实参数估计。。
 贝叶斯决策论与分类器
贝叶斯决策论与分类器




 是标记错误的损失函数)。所以得到优化任务:最小化条件风险R(Ci|x)。。。
是标记错误的损失函数)。所以得到优化任务:最小化条件风险R(Ci|x)。。。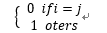
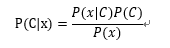 因为样本x 是固定的,所以只需求P(x|C)P(C)即可
因为样本x 是固定的,所以只需求P(x|C)P(C)即可















 528
528

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








