吴恩达【深度学习工程师】学习笔记（五）

吴恩达【深度学习工程师】专项课程包含以下五门课程：

1、神经网络和深度学习；
2、改善深层神经网络：超参数调试、正则化以及优化；
3、结构化机器学习项目；
4、卷积神经网络；
5、序列模型。

今天介绍《神经网络与深度学习》系列第五讲：深层（deep）神经网络。

主要内容：

1、用流程块图的方式详细推导正向传播过程、反向传播过程的输入输出及参数表达式；

2、从提取特征复杂性、计算量的角度两个方面解释了深层神经网络的优势；

3、介绍了超参数的概念，并解释了超参数与参数的区别；

4、将神经网络与人脑做了类比。

1、 深层神经网络

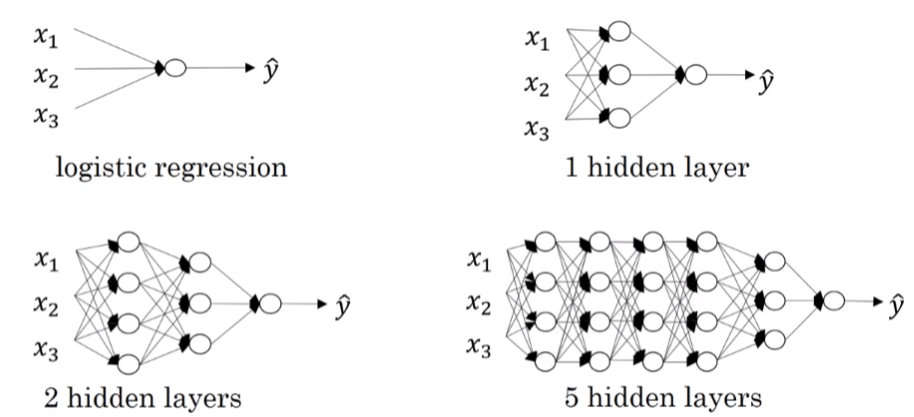
深层神经网络是包含更多的隐藏层神经网络。

如图所示，分别列举了逻辑回归、1个隐层、2个隐层和5个隐层的神经网络模型：

正向传播过程。以4层神经网络为例，对于m个训练样本，其向量化矩阵形式为：

第1层：

Z[1]=W[1]X+b[1]=W[1]A[0]+b[1]

A[1]=g[1](Z[1])

第2层：

Z[2]=W[2]A[1]+b[2]

A[2]=g[2](Z[2])

对于第 l 层，其正向传播过程的 Z[l] 和 A[l] 可以表示为：

Z[l]=W[l]A[l−1]+b[l]

A[l]=g[l](Z[l])

其中 l=1,⋯,L

对于m个训练样本，输入矩阵X的维度是（ n[0],m ）：

W[l]: (n[l],n[l−1])

b[l]: (n[l],1)

在运算 Z[l]=W[l]A[l−1]+b[l] 中， b[l] 会被当成（ n[l],m ）矩阵进行运算，这是由于python的广播特性，且 b[l] 每一列向量都是一样的。 dW[l] 和 db[l] 的维度分别与 W[l] 和 b[l] 的相同。

Z[l] 和 A[l] 的维度：

Z[l]: (n[l],m)

A[l]: (n[l],m)

dZ[l] 和 dA[l] 的维度分别与 Z[l] 和 A[l] 的相同。

2、为什么深层网络表达能力强？

在图像处理领域，深层神经网络随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。如果隐藏层足够多，那么能够提取的特征就越丰富、越复杂，模型的准确率就会越高。

在语音识别领域，浅层的神经元能够检测一些简单的音调，然后较深的神经元能够检测出基本的音素，更深的神经元就能够检测出单词信息。如果网络够深，还能对短语、句子进行检测。

除了从提取特征复杂度的角度来说明深层网络的优势之外，深层网络还有另外一个优点，就是能够减少神经元个数，从而减少计算量。

3、构建网络

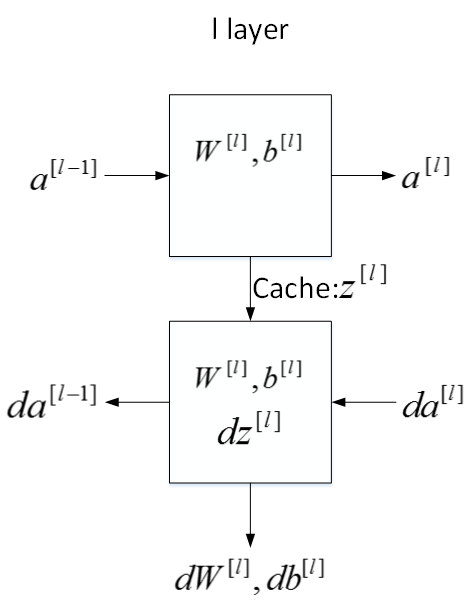
用流程块图来解释神经网络正向传播和反向传播过程。对于第 l 层来说，正向传播中：

输入： a[l−1]

输出： a[l]

参数： W[l],b[l]

缓存变量： z[l]

反向传播过程中：

输入： da[l]

输出： da[l−1],dW[l],db[l]

参数： W[l],b[l]

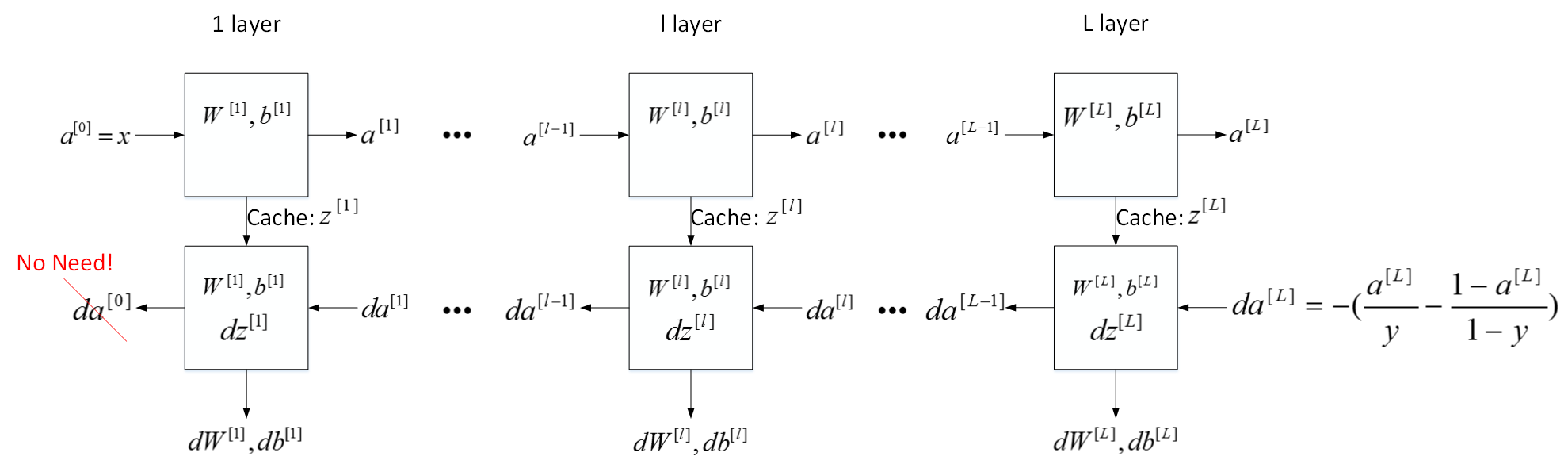
这是第 l 层的流程块图，对于神经网络所有层，整体的流程块图正向传播过程和反向传播过程如下所示：

4、正向反向传播

正向传播过程，m个训练样本，向量化形式为：

Z[l]=W[l]A[l−1]+b[l]

A[l]=g[l](Z[l])

反向传播过程向量化形式为：

dZ[l]=dA[l]∗g[l]′(Z[l])

dW[l]=1mdZ[l]⋅A[l−1]T

db[l]=1mnp.sum(dZ[l],axis=1,keepdim=True)

dA[l−1]=W[l]T⋅dZ[l]

dZ[l]=W[l+1]T⋅dZ[l+1]∗g[l]′(Z[l])

5、参数与超参数

神经网络中的参数就是 W[l] 和 b[l] 。

超参数则是例如学习速率 α ，训练迭代次数N，神经网络层数L，各层神经元个数 n[l] ，激活函数 g(z) 等。

设置最优的超参数常见的做法是选择超参数为一定范围内的值，分别代入神经网络进行训练，测试代价函数随着迭代次数增加的变化，根据结果选择代价最小时对应的超参数值。

6. 跟人脑有什么关系？

神经网络跟人脑机制到底有什么联系呢？

究竟有多少的相似程度？

神经网络分成两个部分：正向和反向传播过程。

神经网络的每个神经元采用激活函数的方式，类似于感知机模型。这种模型与人脑神经元是类似的，可以说是一种非常简化的人脑神经元模型。

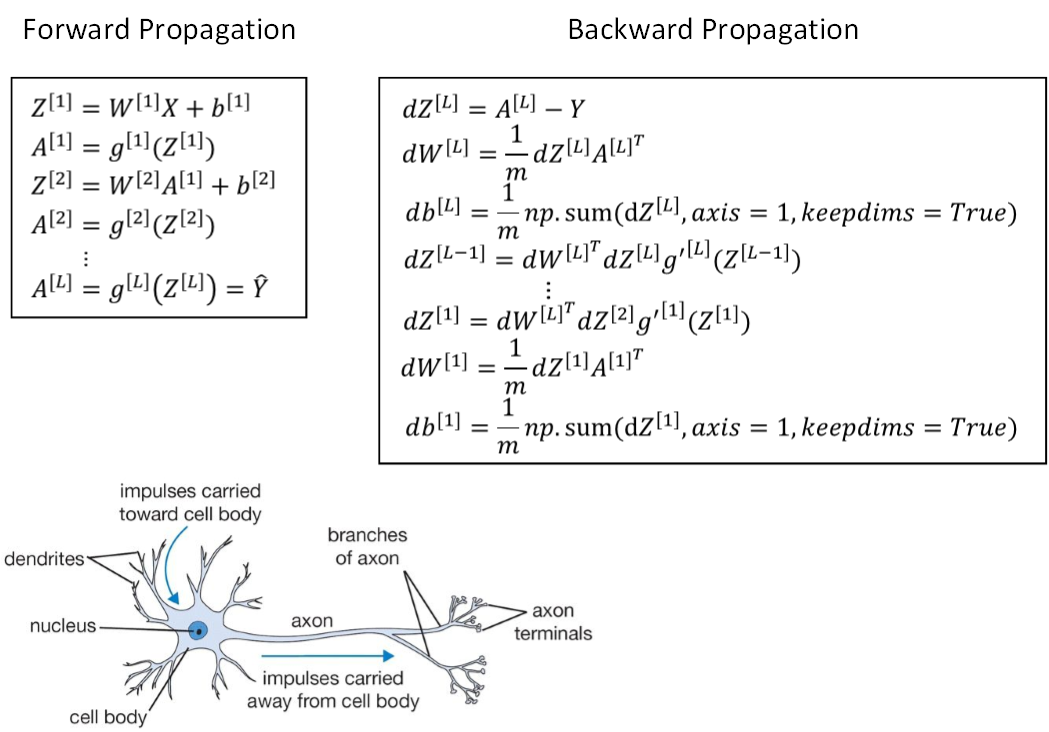
如下图所示，人脑神经元可分为树突、细胞体、轴突三部分。树突接收外界电刺激信号（类比神经网络中神经元输入），传递给细胞体进行处理（类比神经网络中神经元激活函数运算），最后由轴突传递给下一个神经元（类比神经网络中神经元输出）。

但是，人脑神经元的结构和处理方式要复杂的多，神经网络模型只是非常简化的模型。人脑如何进行学习？是否也是通过反向传播和梯度下降算法现在还不清楚，可能会更加复杂。