【15】processing-三角函数（中文）

三角函数

艾拉·格林伯格

 

三角函数（实际上只是几个三角函数）是图形编程的核心。也就是说，如果你和我一样，你可能对trig有模糊的记忆。也许你还记得记忆装置soh-cah-to a，用来记住三角函数和直角三角形之间的关系。这是唤醒你记忆的图表。

•soh代表“正弦等于斜边上的对边。”“对边”是指角度相反的边。

•cah代表“余弦等于斜边上的相邻度。”“相邻”是角度旁边的边。

•toa是指“切线等于相对于相邻点”

 

在图中还应该注意切线等于正弦（θ）而不是余弦（θ）。你可能还记得正弦和余弦在作图时是相似的，它们都形成周期波。只有余弦波在图上移动了一位（90°或π/2），这在技术上称为相移。我完全意识到抽象地处理这些事情是困难的。幸运的是，还有另一个模型，单位圆（如下所示）用于可视化和研究trig函数。

 

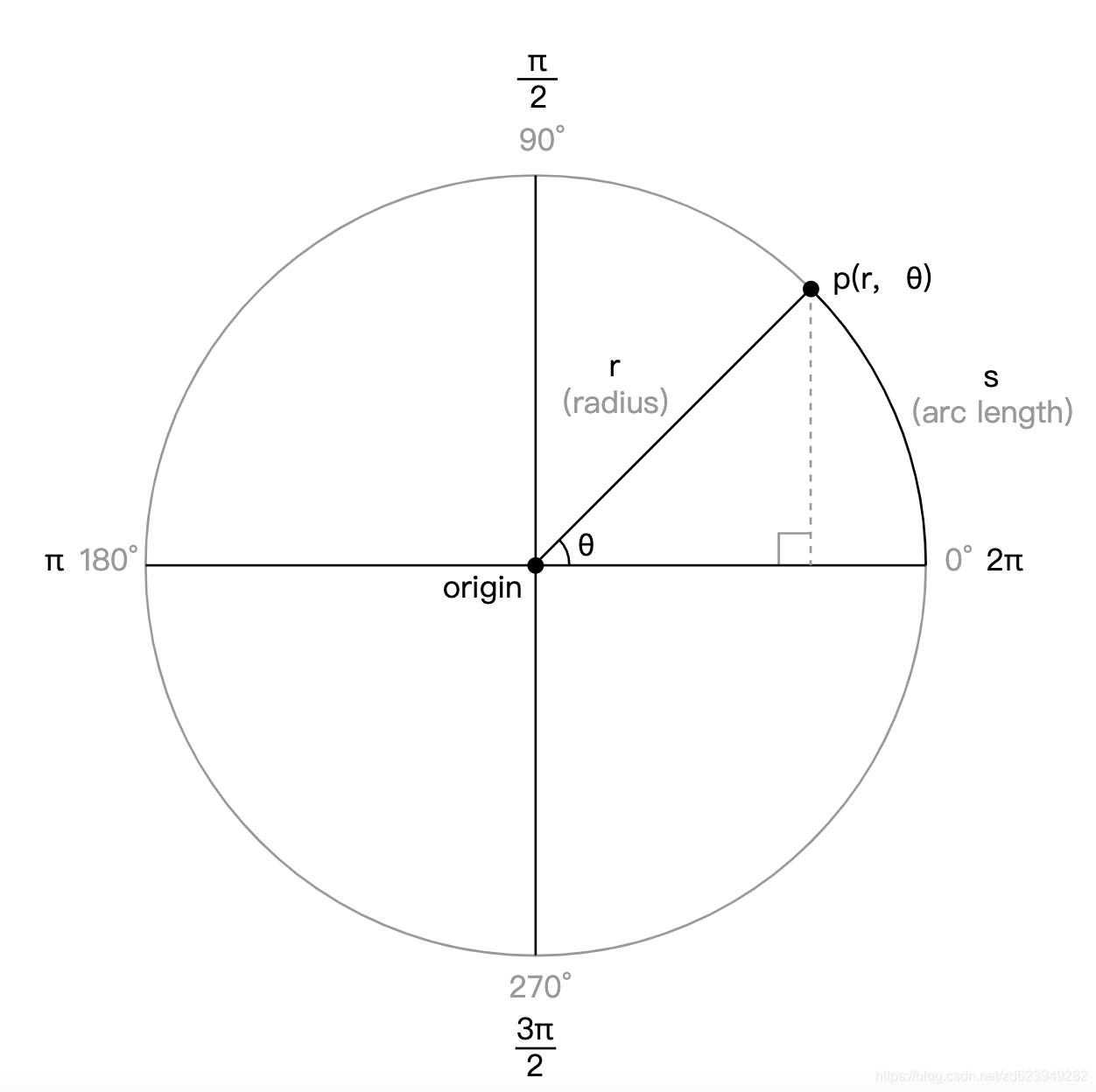
单位圆是一个半径为1个单位长度的圆，因此它的名字很有想象力。使用单位圆时，不使用常规且可信的笛卡尔坐标系；而是使用极坐标系。笛卡尔系统在矩形网格空间中工作得很好，在那里一个点可以通过一个坐标定位，比如（x，y）。相反，在极坐标系中，位置由（r，θ）指定，其中r是半径，θ（希腊字母theta）是旋转角度。单位圆的原点位于其中心，您可以测量从单位圆的右中边缘开始（面向3点钟）并围绕其逆时针方向移动的旋转角度。

 

在单位圆图中，p点位于45°或pi/4。您还可以使用pi来测量单位圆周围的距离，如图所示。在圆的中间（180°）等于π弧度，在圆的四周等于2pi弧度，也等于0弧度，因为圆是连续的，在其开始处结束。π是一个常数，等于圆的周长除以圆的直径，约为3.142。

 

在极坐标系中，使用弧度来测量角度，而不是度数。以弧度表示的旋转角通常称为θ（希腊字母θ）。旋转的弧长由r*θ计算，其中r是半径。在半径为1的单位圆中，θ等于旋转的弧长（单位圆图中的弧s）。知道弧长很好，但大多数时候（在计算机图形学中），你只想知道点相对于单位圆的位置。例如，如果我想围绕单位圆旋转一个点，我需要知道如何在圆中放置和移动该点。对于单位圆来说，这是一个非常简单的任务，而且正是trig的用途。

 

三角函数和单位圆之间有一个非常简单的关系。注意，在单位圆图中，从椭圆上的p点开始，单位圆内形成直角三角形。这会立刻让你想起老毕达哥拉斯。还要注意r（半径）是直角三角形的斜边。此外，您现在还知道，使用trig函数，可以使用theta和任意一侧（对边、相邻边或斜边）来求解三角形的其余部分。对于我们的目的，这些关系的最大好处是，要将极坐标系中的p点转换为笛卡尔坐标系（监视器使用的系统），可以使用以下简单表达式：

 

x = cosine(theta) * radius
y = sine(theta) * radius

 

这些看似谦逊的小表达方式非常强大，可以用于各种表达和有机的目的。

以下是在处理过程中如何实际使用trig函数：

 

 

float x = cos(radians(angle)) * radius;
float y = sin(radians(angle)) * radius;

注意每个trig函数调用中的函数调用(radians(angle))（弧度（角度））。记住θ是用弧度来测量的，在极坐标系中。但是，在笛卡尔坐标系中，以度数为单位。要在弧度和度数之间进行转换，或者在弧度和度数之间进行转换，可以使用以下表达式：

 

theta = angle*pi/180
angle = theta*180/pi

 

或者更好的方法是，使用Processing的便捷转换功能：

 

 

theta = radians(angle)
angle = degrees(theta)

最后，我还提供了一个处理示意图，演示了单位圆和正弦函数之间的关系：

 

 

float px, py, px2, py2;
float angle, angle2;
float radius = 50;
float frequency = 2;
float frequency2 = 2;
float x, x2;

void setup(){
  size(600, 200);
  background (127);
}

void draw(){
  background (127);
  noStroke();
  fill(255);
  ellipse(width/8, 75, radius*2, radius*2);
  
  // 围绕圆旋转矩形
  px = width/8 + cos(radians(angle))*(radius);
  py = 75 + sin(radians(angle))*(radius);
  fill(0);

  rect (px, py, 5, 5);
  stroke(100);
  line(width/8, 75, px, py);
  stroke(200);

  //继续重新初始化为0，以避免
    //重绘时闪烁
  angle2 = 0;

  // 绘制静态曲线-y=sin（x）
  for (int i = 0; i< width; i++){
    px2 = width/8 + cos(radians(angle2))*(radius);
    py2 = 75 + sin(radians(angle2))*(radius);
    point(width/8+radius+i, py2);
    angle2 -= frequency2;
  }

  //沿正弦曲线发送小椭圆
    //说明圆与波的关系
  noStroke();
  ellipse(width/8+radius+x, py, 5, 5);
  angle -= frequency;
  x+=1;

  //当小椭圆到达窗口的末端时，
    //将变量设置回0
  if (x >= width-60) {
    x = 0;
    angle = 0;
  }

  //画波与圆路径连接的动力线
  stroke(50);
  line(px, py, width/8+radius+x, py);

  //输出计算到屏幕
  text("y = sin x", 35, 185);
  text("px = " + px, 105, 185);
  text("py = " + py, 215, 185);
}