再谈大量数据去重：字典树（Trie）和外排序（External Sorting）

时隔多年又再次见到这个问题，不得不说是一个经久不衰的问题。与友人讨论时，感叹这个问题反复在不同场合被不同人提起，但每次探索答案时，又总不能获得一个“标准答案”。最早我第一次遇到这个问题时，我给出的令我自己可以满意的答案是：大量数据去重：Bitmap和布隆过滤器(Bloom Filter)。在一定程度上，它确实大大缓解了“有限空间”对hash实现的限制。但是回头一看，布隆过滤器作为工程实现（带有一定错误率），它不应该是一道算法题的解决思路——即最优解。所以，今次再次谈及此题，又有了一些别的思考。时移事易，今日的题设有了一些变化：

有A、B两份大文件，按行分隔，放置了数以亿记的URL。请你给出一个算法，找出所有两份文件同时出现的URL。内存空间有限，你只能适用512MB内存。

换汤不换药，单纯的逐行读取文件并不需要一次性加载整份文件。因此我们以B文件为逐行读取的对象，那么每一个URL，我们需要判断它是否存在于A中，这个操作越快越好。如果空间不限，我们可以把A加载到内存，创建一个哈希表——单纯的位图并不适用与这种场景，因为URL即便映射到某个位上，为了解决碰撞问题，我们仍然需要存储URL本身，以便碰撞发生时进行开放地址（Open addressing）或链地址（Separate chaining）¹。这种做法，平均上仍然可以在O(1)时间内查到一个URL存在与否。但是，空间上所有字符都需要进入内存，空间复杂度为$O(NL)$，$N$为A文件的行数，$L$为URL的平均长度。RFC7230²中提及实践中建议客户端和服务器支持8000字节的URL，而大多数浏览器支持2000字节的URL³。

空间压缩

和位图类似，遇到这类空间有限的问题，我们总是会先想到如何压缩空间到极致、而不是优先考虑牺牲一部分东西——布隆过滤器牺牲了正确率，以及我们即将提到的外排序牺牲了时间。位图相当于为每个整型值找了一个单独的比特来表示其存在性，而对于URL，我们能做些什么呢？

编码

如上图所示，URL是一种高度结构化的字符串⁴，从某种角度上可以进行编码压缩。

• 对于scheme部分，有限的几种协议如http、https、ftp等，可以用一个字节进行表示；
• 对于host部分，以ip形式出现的host实际是“点分十进制”表示的四个字节，“127.0.0.1”可以直接被压缩成十六进制数0x0F000001；
• 对于port部分，可能的端口号为0~65535，可以用两个字节表示；
• 从定长码的角度，URL可能字符集为84个字符⁵：
  {   c h   ∣   c h   i n   A   t o   Z , a   t o   z , 0   t o   9   a n d   − .   : / ? # [ ] @ ! $ & ′ ( ) ∗ + , ; = } \{\ ch\ |\ ch\ in\ A\ to\ Z,a\ to\ z,0\ to\ 9\ and\ -._~:/?\#[]@!\$\&'()*+,;=\} { ch ∣ ch in A to Z,a to z,0 to 9 and −. ​:/?#[]@!$&′()∗+,;=}
  严格上来说，并不需要一个字节来表示一个字符，可以将每个字符映射到一个7比特码本（码空间大小为128），这样可以将空间消耗缩小为原来的7/8；
• 从变长码的角度，URL也是一种类字词拼接的文本形式，霍夫曼编码可以对URL进行无损压缩。

压缩之后的字节流可以成倍缩短URL的长度，但是仍然需要成百字节来构成一个URL。如果我们用一个很不保守的长度50字节来估算一个URL，1亿条URL（假设各不相同、没有重复）需要空间：
$$50Bytes\ast 100000000\approx 5\ast 2^{30}Bytes=5GB$$
这看起来并不是很大，但是仍然没法在512MB如此严酷的内存条件下完成任务。

字典树（Trie）

字典树（Trie）也叫前缀树，它是我这次看到这题时，第一个想到的解决办法。首先，URL这种高度结构化的、自带前缀叠合属性的文本串，用字典树这种前缀结构时再合适不过了。本身来说，每个网站在有限的URI内，实际上是把自身有限的资源按目录结构有序放置在一个多叉树下，就如文件系统一样，所以经常会出现前缀相同的资源：如www.baidu.com/abc/1.txt和www.baidu.com/abc/2.txt，他们实际的差异就是最后的资源文件名，前缀则完全相同。当然，这个假设是建立在输入URL都是有效的URL的前提下——如来源于爬虫爬取等，当然这也是最常见的实际应用。如果是随机暴力拼装的URL，则不会具备任何前缀特性，访问之后对端服务器大概率会丢给你一个404。假定，A文件有大量来自于http://www.google.com/mail、http://www.google.com/document以及http://www.facebook.com/的链接，以字典树的形式会被压缩为：


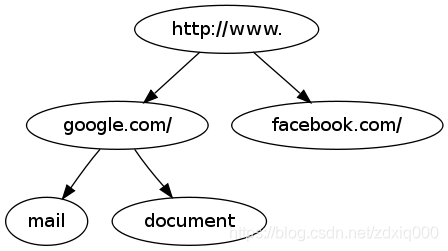
这种形式的压缩就不再局限于URL本身了，而是一种全局的合并与压缩。所有来自http://www.google.com以及http://www.facebook.com，会共享同样的前缀。如果有1000万条来自Google的URL，节省的空间相当于：
$$“www.google.com”.length()\ast (10000000-1)B\approx 140MB$$
如果所有1亿个URL都是携带“www”前缀的话，就能压缩掉大约300MB。很明显，字典树和上一节提到的编码压缩并不冲突——www.baidu.com不论如何压缩，不论是定长码或是变长码，最终都是逐字符压缩，没有改变顺序，也就不会改变URL的前缀特性，这100万条URL就可以进一步压缩合并。

另一方面，字典树的时间复杂度在最坏情况下需要把匹配串完整扫描一遍，也就是$O(L)$，$L$为字符串长度；比哈希表稍差，但是别忘了哈希值的计算，严格上来说也需要遍历模式串。所以，我个人认为查询时间复杂度应该是相同的。

因此字典树在时间没有劣化的前提下，进一步缩小了内存使用。可是，与位图一样，我们也遇到了瓶颈，不论是哈希表还是前缀树，在严苛的内存限制下，是没办法解决问题的。既然空间利用已经到达了极限，就只能在时间上做妥协了。

外排序（External Sorting）

External sorting is a class of sorting algorithms that can handle massive amounts of data. External sorting is required when the data being sorted do not fit into the main memory of a computing device (usually RAM) and instead they must reside in the slower external memory, usually a hard disk drive. Thus, external sorting algorithms are external memory algorithms and thus applicable in the external memory model of computation.

从某种意义上说，外排序不是一种特定的算法，只是一类算法的统称。只要能利用除了内存以外的外部存储解决大量数据排序，尤其是放不进内存的数据量（do not fit into the main memory），这种算法就可以称为外排序。虽然经常在“大量数据去重”的问题下看到外排序，但是很多时候并没有人说清具体怎么解决这个问题，也可能就是因为它并不是一种特定算法，而是一种定义——字典树就不是一种外排序，极端情况下它仍然需要把整份A文件的字符放到内存里，它没办法利用外部存储解决这种极端情况。

但严格上讲，如果利用虚拟内存技术，所有的数据结构都可以放在硬盘上，代价就是会增加大量的硬盘访问，时间复杂度会增加一个极大的常量，这种解决思路并不值得提倡。

排序与去重

一份已排好序的文件，要做去重可以说是相当容易了。因为你只需要对比上下两行相邻文本即可。那倘若A、B两份文件都已排好序（假设是字典序），这个时候两个行级指针加上简单的比较，就可以很容易获得两者的交集（重复的URL）——这也是一个很简单的二路归并。

while ptr_b != EOF || ptr_a != EOF:
do
	res <- compare(&ptr_a, &ptr_b)
	if res == 0
		do find_a_duplicate_url(ptr_a)
	else if res > 0
		do append_to_merged_file(ptr_a)
		   ptr_a <- prt_a + 1
	else
		do append_to_merged_file(ptr_b)
		   ptr_b <- ptr_b + 1

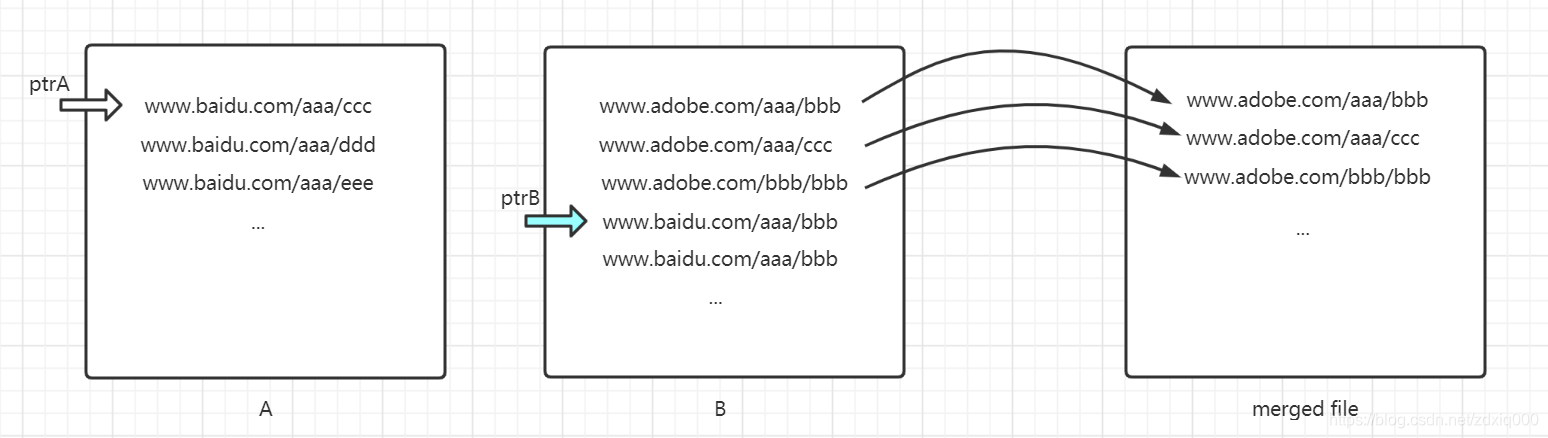
同样的，如果有很多份文件已经排好序，你也可以在合并文件的同时达到去重的目的，这也是外部归并排序（External Merge Sorting）的关键步骤之一。所以，排序就是去重的充分条件，外排序正是去重的关键入口。

那么，如何实现排序呢？

Unix系统中的sort

一提到几百G的文件，Unix/类Unix系统可就不困了。几十上百G的文件，排排序、去去重、数数数，这不是家常便饭嘛：

sort file.txt | uniq -c

诶，人家这几G文件不是随便排？还有几百个守护进程常驻内存，怎么就没见Unix系统原地爆炸呢[手动狗头]。看来有必要去翻一翻这个实现，它可能就是解决问题的关键。这个回答里⁶ 提到了，Unix实际上使用的是一种多路归并的外部排序算法（External R-Way Merge Sorting Algorithm）。这里的“多路归并”实际上和上一小节提到二路归并类似，代表的是多路归并，当有多于两份文件时，我们可以利用堆等优先结构，同时合并这些文件。在wertarbyte的仓库里，我们可以找到sort.c的实现⁷：

/* Merge lines from FILES onto OFP.  NTEMPS is the number of temporary
   files (all of which are at the start of the FILES array), and
   NFILES is the number of files; 0 <= NTEMPS <= NFILES <= NMERGE.
   Close input and output files before returning.
   OUTPUT_FILE gives the name of the output file.
   Return the number of files successfully merged.  This number can be
   less than NFILES if we ran low on file descriptors, but in this
   case it is never less than 2.  */

static size_t
mergefiles (struct sortfile *files, size_t ntemps, size_t nfiles,
            FILE *ofp, char const *output_file)
{
  FILE **fps;
  size_t nopened = open_input_files (files, nfiles, &fps);
  if (nopened < nfiles && nopened < 2)
    die (_("open failed"), files[nopened].name);
  mergefps (files, ntemps, nopened, ofp, output_file, fps);
  return nopened;
}

/* Merge lines from FILES onto OFP.  NTEMPS is the number of temporary
   files (all of which are at the start of the FILES array), and
   NFILES is the number of files; 0 <= NTEMPS <= NFILES <= NMERGE.
   FPS is the vector of open stream corresponding to the files.
   Close input and output streams before returning.
   OUTPUT_FILE gives the name of the output file.  If it is NULL,
   the output file is standard output.  */

static void
mergefps (struct sortfile *files, size_t ntemps, size_t nfiles,
          FILE *ofp, char const *output_file, FILE **fps)
{
  ...
  /* Repeatedly output the smallest line until no input remains. */
  while (nfiles) { ... }
  ...
}

sort.c的实际实现相当复杂，后续我们会看到外部排序由于涉及到文件描述符和反复的文件读取，需要考虑各种各样的异常情况。但是，管中窥豹，我们仍然可以看出sort.c对大文件进行了分割，并且产生了很多中间文件，而在最后由mergefps将其及进行了多路归并。

二路归并（2-Way Merge）与多路归并（K-Way Merge）

二路归并（2-Way Merge）又被称为“binary merge”，是课本上的归并排序的主要组成部分之一——先把原数组不断分割到最小单元（仅含一个元素的子数组），然后依次两两合并，直到得到排序后的数组。二路归并的递归调用树如同二叉树，每一层合并都需要遍历整个数组，这样的遍历需要$lo{g}_{2}N$次，因此最终复杂度是$O(NlogN)$。

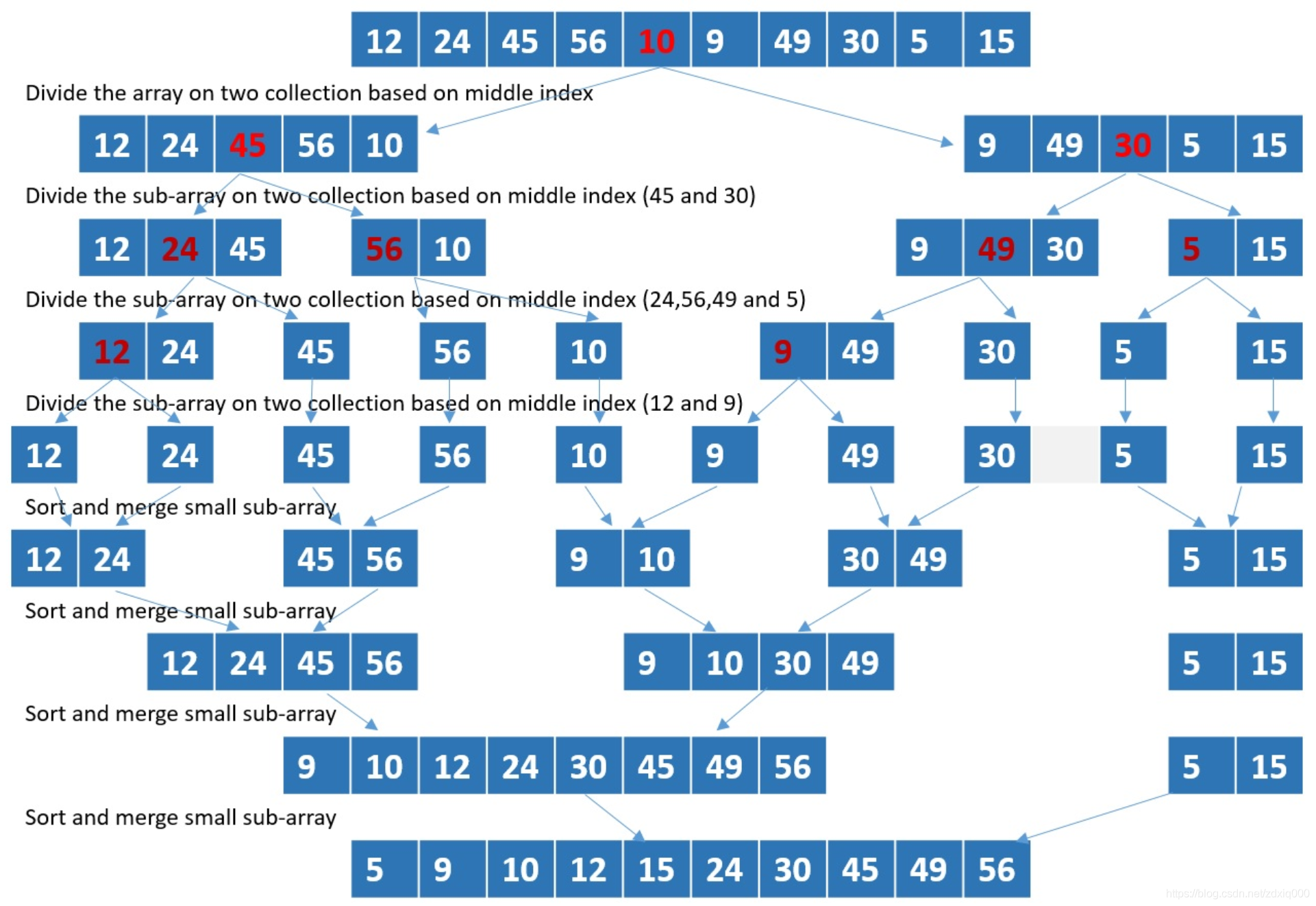
这不禁引起人的思考，那这里我们为什么不用多路归并（K-Way Merge）达到我们的目的呢？我们以$K(K<=N)$路归并为例，我们的层数将变成$lo{g}_{K}N$；在不引入额外的空间复杂度的条件下，我们同时合并K个有序数组，每次需要找到K个数中最小的那个数，需要$K-1$次比较，最终完成每一层所有元素的合并，时间复杂度为$O(KN)$，最终我们得到K路归并的时间复杂度为：
$$O(KNlo{g}_{K}N)=O(NlogN\frac{K}{logK})$$
我们会发现随着$K$增大，时间复杂度是递增的（求导会发现有拐点，大约在2~3之间，我们的定义域$[2,+\inf )$上是凹函数），这也是为什么我们最常使用的是二路归并，它渐渐也成为了归并算法的核心。而从实现层面上，二路归并也要简单得多。多路归并是一个非常复杂的议题，也有许多不同实现方式，但我们上面的讨论都是针对于所有数据都放在内存里进行合并的情况，如果场景切换到外排序，我们为什么要使用多路归并呢？

外部多路归并排序算法

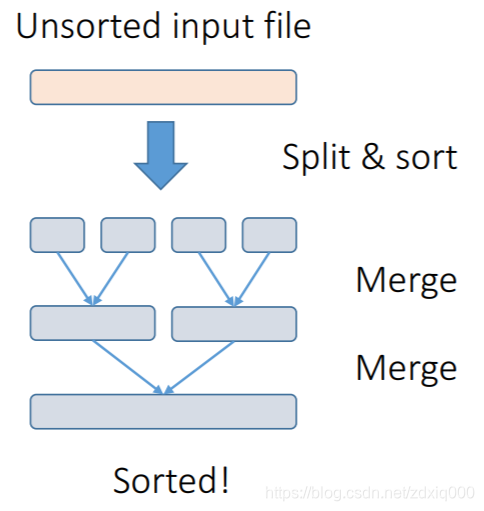
外部排序的关键在于利用硬盘。多路归并开始时，文件通常很小，例如只有一行的文件，它自然就是有序的，于是我们可以开始进行归并；而从另一个角度，当文件拆得足够小之后，我们不需要继续拆解，只要这个文件足以放置到内存中排序，我们就可以得到一份有序文件，作为归并的原始文件。这也正是外部归并算法的核心——在近乎取之不尽用之不竭的硬盘上，我们有足够多的空间去保存通过内存排序排好的文件，而归并算法的特性决定了，我们可以逐行逐次读取文件进行归并，这样我们其实并不需要很大的内存就可以完成整个归并过程。

• 第一步，我们把原始大文件分割成合适的份数，分别在内存中完成排序后，存储到硬盘上。外部归并排序算法的内存瓶颈就在第一步生成有序的小文件，称为临时文件（temporary files），也就是图里的Run 1 ~ Run n。这步排序是可以通过内存完成的，因此每份文件的大小大约就是内存大小。
• 第二步，逐行逐文件完成文件的有序归并。内存中只需要有一定的空间来保存文件描述符、当前行，并以适当结构维护n份文件中最小的那一行并追加到最终输出，所以这一步空间可大可小。但由于硬盘访问本身是一个大时间常数操作，所以应做到应读尽读、应载尽载，尽可能将文件内容预先加载到内存中。

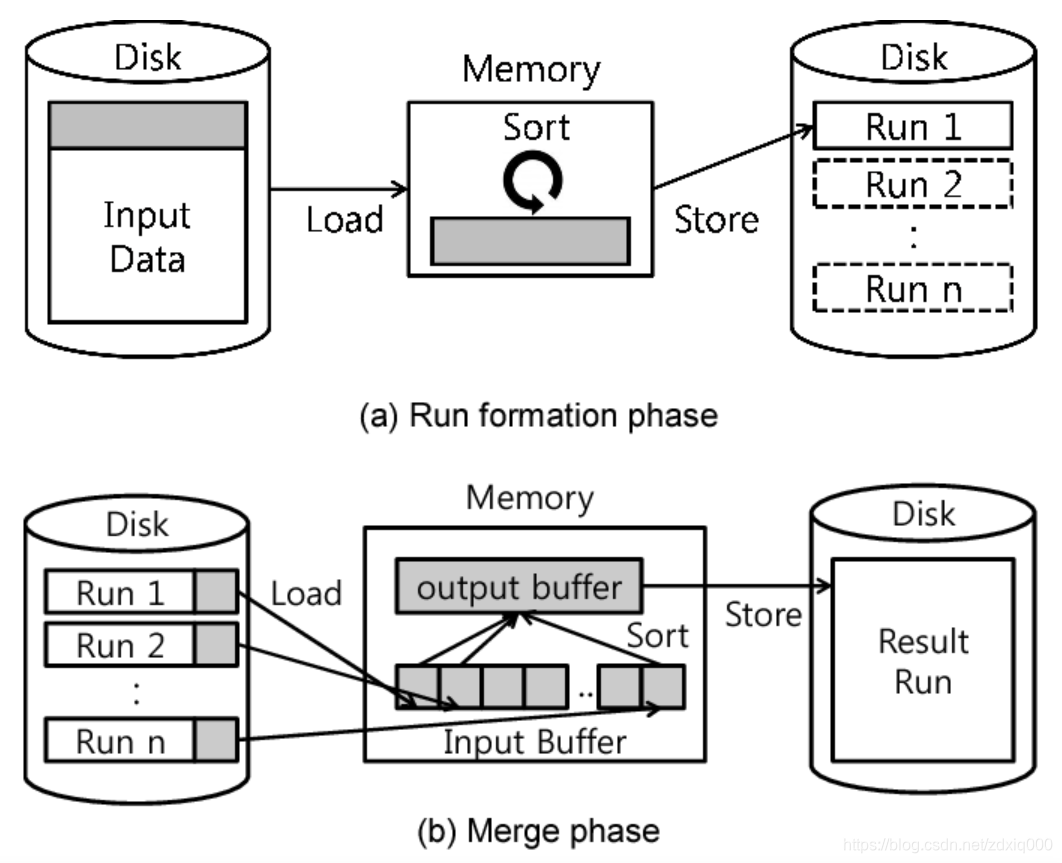
我们来看一个具体例子，这个例子来源于维基百科⁸，我仅做翻译：

假设我们需要利用100MB内存，对900MB的文件进行排序。

1. 将100MB数据读入内存，利用快速排序对其进行排序。
2. 将结果写入硬盘。
3. 重复1和2，直到所有数据都所有数据都保存为有序的100MB小文件（一共900MB / 100MB = 9份文件），接下来需要将这些小文件合并成一份大文件。
4. 从每份已排序的小文件头部读取10MB（= 100MB / (9 + 1)）数据到内存，一共产生9个输入缓冲区（Input Buffer），剩下的10MB作为输出缓冲区（Output Buffer。实践中发现，输出缓冲区更大一些会有更好性能，此处为计算简便先取9:1。
5. 通过9路归并，把结果保存到输出缓冲区。一旦输出缓冲区满，则将所有数据输出到硬盘（最终的大文件中）；一旦9个输入缓冲区中的一个空了，则从对应文件里再读取10MB数据，直到这个文件没有数据为止。注意，我们是顺序地、逐步地读取每一份小文件，没有必要一次性加载整个小文件内容——同一时间内，每一份小文件最多驻留内存的数据量为10MB。

假定，可用内存为$M$，临时文件（分块）数量为$P$，源文件大小为$N=M\ast P)$。则排序部分，我们需要对$P$份文件分别进行快排，时间为$O(PMlogM)$；合并部分，我们执行$P$路归并，这里假定比较元素大小时我们使用小顶堆，则第二部分的时间复杂度为$O(NlogP)$。整个算法的时间复杂度为：
$$O(NlogM+NlogP)=O(NlogMP)=O(NlogN)$$
这也是维基百科指出的复杂度——高效的外排序的时间复杂度和内排序相同⁸。看似只和源文件大小有关？那岂不是我们选取多大的内存都无关紧要，但实际上，类似的问题，内存一定时越大越好，极小的内存下，需要频繁读写（分块极多）硬盘，性能一定会快速劣化。其实，以上的计算有一个很大的漏洞，即忽略了硬盘和内存的存取速度在数量级上的差异。第一步中内存排序的存取实际上时非常快的，而耗时的事情其实在于硬盘读写。外存储器算法（External Memory Algorithm）⁹给出了一个可以量化的模型来评估这类涉及到不同层次数据存储时的算法复杂度：

The cache on the left holds $\frac{M}{B}$ blocks of size $B$ each, for a total of $M$ objects. The external memory on the right is unbounded.

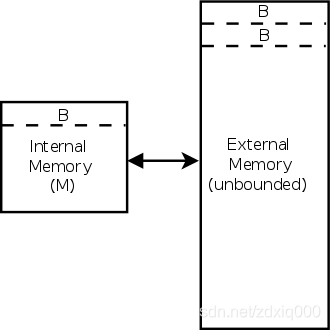
这个模型强调以磁盘I/O次数来评估归并算法的复杂度。模型将有限的内存储（大小为$M$）和无界的外存储按固定的分块（chunk）大小$B$来分割。每次从硬盘中加载大小为$B$的数据，需要进行一次I/O；而输出缓冲区满，又将大小为$B$的数据输出到硬盘，此为第二次I/O。因此，每个块需要两次I/O，如果一共有$N$大小的外存数据需要排序，共需$2\ast N/B$次I/O。整体上仍然遵循归并排序的复杂度¹⁰：
$$O\left(\frac{N}{B}{\log }_{\frac{M}{B}}\frac{N}{B}\right)$$

总结

外部排序是一大类在实际应用中更具实用性的算法。除了外部归并排序，还有快排的变种分布式排序等，他们的渐进时间复杂度都能达到相同数量级。而完成排序后，文件的去重就可以转变为简单的全文扫描。至此，大量数据排序在单机、多级缓存体系下，已经得到了很好的解决。

---

1. https://en.wikipedia.org/wiki/Hash_table ↩︎

2. https://datatracker.ietf.org/doc/html/rfc7230#section-3.1.1 ↩︎

3. https://stackoverflow.com/questions/417142/what-is-the-maximum-length-of-a-url-in-different-browsers ↩︎

4. https://en.wikipedia.org/wiki/URL ↩︎

5. https://stackoverflow.com/questions/1547899/which-characters-make-a-url-invalid/1547940#1547940 ↩︎

6. https://stackoverflow.com/questions/930044/how-could-the-unix-sort-command-sort-a-very-large-file ↩︎

7. https://github.com/wertarbyte/coreutils/blob/master/src/sort.c ↩︎

8. https://en.wikipedia.org/wiki/External_sorting ↩︎ ↩︎

9. https://en.wikipedia.org/wiki/External_memory_algorithm ↩︎

10. https://thodrek.github.io/cs564-fall17/lectures/lecture-11/Lecture_11_ExtSort.pdf ↩︎