关于CPU Cache -- 程序员需要知道的那些事

最新推荐文章于 2024-08-03 16:24:11 发布

zdy0_2004

最新推荐文章于 2024-08-03 16:24:11 发布

阅读量598

点赞数

分类专栏： C++ 文章标签：操作系统

C++ 专栏收录该内容

202 篇文章 4 订阅

订阅专栏

关于CPU Cache -- 程序员需要知道的那些事

http://www.cnblogs.com/cenalulu/p/4340891.html

本文将介绍一些作为程序猿或者IT从业者应该知道的CPU Cache相关的知识。本章从“为什么会有CPU Cache”，“CPU Cache的大致设计架构”，“几个认识CPU Cache的实验”多个方面介绍作为一个程序员所需知道的关于CPU Cache的基础知识。并通过知识总结出，作为程序员了解这些知识后能对平时开发带来什么帮助

文章欢迎转载，但转载时请保留本段文字，并置于文章的顶部
作者：卢钧轶(cenalulu)
本文原文地址：http://cenalulu.github.io/linux/all-about-cpu-cache/

本博客已经迁移至：

http://cenalulu.github.io/

为了更好的体验，请通过此链接阅读：

http://cenalulu.github.io/linux/all-about-cpu-cache/

先来看一张本文所有概念的一个思维导图

为什么要有CPU Cache

随着工艺的提升最近几十年CPU的频率不断提升，而受制于制造工艺和成本限制，目前计算机的内存主要是DRAM并且在访问速度上没有质的突破。因此，CPU的处理速度和内存的访问速度差距越来越大，甚至可以达到上万倍。这种情况下传统的CPU通过FSB直连内存的方式显然就会因为内存访问的等待，导致计算资源大量闲置，降低CPU整体吞吐量。同时又由于内存数据访问的热点集中性，在CPU和内存之间用较为快速而成本较高的SDRAM做一层缓存，就显得性价比极高了。

为什么要有多级CPU Cache

随着科技发展，热点数据的体积越来越大，单纯的增加一级缓存大小的性价比已经很低了。因此，就慢慢出现了在一级缓存(L1 Cache)和内存之间又增加一层访问速度和成本都介于两者之间的二级缓存(L2 Cache)。下面是一段从What Every Programmer Should Know About Memory中摘录的解释：

Soon after the introduction of the cache the system got more complicated. The speed difference between the cache and the main memory increased again, to a point that another level of cache was added, bigger and slower than the first-level cache. Only increasing the size of the first-level cache was not an option for economical rea- sons.

此外，又由于程序指令和程序数据的行为和热点分布差异很大，因此L1 Cache也被划分成L1i (i for instruction)和L1d (d for data)两种专门用途的缓存。

什么是Cache Line

Cache Line可以简单的理解为CPU Cache中的最小缓存单位。目前主流的CPU Cache的Cache Line大小都是64Bytes。假设我们有一个512字节的一级缓存，那么按照64B的缓存单位大小来算，这个一级缓存所能存放的缓存个数就是512/64 = 8个。具体参见下图：

为了更好的了解Cache Line，我们还可以在自己的电脑上做下面这个有趣的实验。

下面这段C代码，会从命令行接收一个参数作为数组的大小创建一个数量为N的int数组。并依次循环的从这个数组中进行数组内容访问，循环10亿次。最终输出数组总大小和对应总执行时间。

#include "stdio.h"
#include <stdlib.h>
#include <sys/time.h>

long timediff(clock_t t1, clock_t t2) {
    long elapsed;
    elapsed = ((double)t2 - t1) / CLOCKS_PER_SEC * 1000;
    return elapsed;
}

int main(int argc, char *argv[])
#*******
{

    int array_size=atoi(argv[1]);
    int repeat_times = 1000000000;
    long array[array_size];
    for(int i=0; i<array_size; i++){
        array[i] = 0;
    }
    int j=0;
    int k=0;
    int c=0;
    clock_t start=clock();
    while(j++<repeat_times){
        if(k==array_size){
            k=0;
        }
        c = array[k++];
    }
    clock_t end =clock();
    printf("%lu\n", timediff(start,end));
    return 0;
}

如果我们把这些数据做成折线图后就会发现：总执行时间在数组大小超过64Bytes时有较为明显的拐点（当然，由于博主是在自己的Mac笔记本上测试的，会受到很多其他程序的干扰，因此会有波动）。原因是当数组小于64Bytes时数组极有可能落在一条Cache Line内，而一个元素的访问就会使得整条Cache Line被填充，因而值得后面的若干个元素受益于缓存带来的加速。而当数组大于64Bytes时，必然至少需要两条Cache Line，继而在循环访问时会出现两次Cache Line的填充，由于缓存填充的时间远高于数据访问的响应时间，因此多一次缓存填充对于总执行的影响会被放大，最终得到下图的结果：

如果读者有兴趣的话也可以在自己的linux或者MAC上通过gcc cache_line_size.c -o cache_line_size编译，并通过./cache_line_size执行。

了解Cache Line的概念对我们程序猿有什么帮助？
我们来看下面这个C语言中常用的循环优化例子
下面两段代码中，第一段代码在C语言中总是比第二段代码的执行速度要快。具体的原因相信你仔细阅读了Cache Line的介绍后就很容易理解了。

for(int i = 0; i < n; i++) {
    for(int j = 0; j < n; j++) {
        int num;    
        //code
        arr[i][j] = num;
    }
}

for(int i = 0; i < n; i++) {
    for(int j = 0; j < n; j++) {
        int num;    
        //code
        arr[j][i] = num;
    }
}

CPU Cache 是如何存放数据的

你会怎么设计Cache的存放规则

我们先来尝试回答一下那么这个问题：

假设我们有一块4MB的区域用于缓存，每个缓存对象的唯一标识是它所在的物理内存地址。每个缓存对象大小是64Bytes，所有可以被缓存对象的大小总和（即物理内存总大小）为4GB。那么我们该如何设计这个缓存？

如果你和博主一样是一个大学没有好好学习基础/数字电路的人的话，会觉得最靠谱的的一种方式就是：Hash表。把Cache设计成一个Hash数组。内存地址的Hash值作为数组的Index，缓存对象的值作为数组的Value。每次存取时，都把地址做一次Hash然后找到Cache中对应的位置操作即可。
这样的设计方式在高等语言中很常见，也显然很高效。因为Hash值得计算虽然耗时(10000个CPU Cycle左右)，但是相比程序中其他操作（上百万的CPU Cycle）来说可以忽略不计。而对于CPU Cache来说，本来其设计目标就是在几十CPU Cycle内获取到数据。如果访问效率是百万Cycle这个等级的话，还不如到Memory直接获取数据。当然，更重要的原因是在硬件上要实现Memory Address Hash的功能在成本上是非常高的。

为什么Cache不能做成Fully Associative

Fully Associative 字面意思是全关联。在CPU Cache中的含义是：如果在一个Cache集内，任何一个内存地址的数据可以被缓存在任何一个Cache Line里，那么我们成这个cache是Fully Associative。从定义中我们可以得出这样的结论：给到一个内存地址，要知道他是否存在于Cache中，需要遍历所有Cache Line并比较缓存内容的内存地址。而Cache的本意就是为了在尽可能少得CPU Cycle内取到数据。那么想要设计一个快速的Fully Associative的Cache几乎是不可能的。

为什么Cache不能做成Direct Mapped

和Fully Associative完全相反，使用Direct Mapped模式的Cache给定一个内存地址，就唯一确定了一条Cache Line。设计复杂度低且速度快。那么为什么Cache不使用这种模式呢？让我们来想象这么一种情况：一个拥有1M L2 Cache的32位CPU，每条Cache Line的大小为64Bytes。那么整个L2Cache被划为了1M/64=16384条Cache Line。我们为每条Cache Line从0开始编上号。同时64位CPU所能管理的内存地址范围是2^32=4G，那么Direct Mapped模式下，内存也被划为4G/16384=256K的小份。也就是说每256K的内存地址共享一条Cache Line。但是，这种模式下每条Cache Line的使用率如果要做到接近100%，就需要操作系统对于内存的分配和访问在地址上也是近乎平均的。而与我们的意愿相反，为了减少内存碎片和实现便捷，操作系统更多的是连续集中的使用内存。这样会出现的情况就是0-1000号这样的低编号Cache Line由于内存经常被分配并使用，而16000号以上的Cache Line由于内存鲜有进程访问，几乎一直处于空闲状态。这种情况下，本来就宝贵的1M二级CPU缓存，使用率也许50%都无法达到。

什么是N-Way Set Associative

为了避免以上两种设计模式的缺陷，N-Way Set Associative缓存就出现了。他的原理是把一个缓存按照N个Cache Line作为一组（set），缓存按组划为等分。这样一个64位系统的内存地址在4MB二级缓存中就划成了三个部分（见下图），低位6个bit表示在Cache Line中的偏移量，中间12bit表示Cache组号（set index），剩余的高位46bit就是内存地址的唯一id。这样的设计相较前两种设计有以下两点好处：

给定一个内存地址可以唯一对应一个set，对于set中只需遍历16个元素就可以确定对象是否在缓存中（Full Associative中比较次数随内存大小线性增加）
每2^18(512K)*64=32M的连续热点数据才会导致一个set内的conflict（Direct Mapped中512K的连续热点数据就会出现conflict）

addr

为什么N-Way Set Associative的Set段是从低位而不是高位开始的

下面是一段从How Misaligning Data Can Increase Performance 12x by Reducing Cache Misses摘录的解释：

The vast majority of accesses are close together, so moving the set index bits upwards would cause more conflict misses. You might be able to get away with a hash function that isn’t simply the least significant bits, but most proposed schemes hurt about as much as they help while adding extra complexity.

由于内存的访问通常是大片连续的，或者是因为在同一程序中而导致地址接近的（即这些内存地址的高位都是一样的）。所以如果把内存地址的高位作为set index的话，那么短时间的大量内存访问都会因为set index相同而落在同一个set index中，从而导致cache conflicts使得L2, L3 Cache的命中率低下，影响程序的整体执行效率。

了解N-Way Set Associative的存储模式对我们有什么帮助

了解N-Way Set的概念后，我们不难得出以下结论：2^(6Bits <Cache Line Offset> + 12Bits <Set Index>) = 2^18 = 512K。即在连续的内存地址中每512K都会出现一个处于同一个Cache Set中的缓存对象。也就是说这些对象都会争抢一个仅有16个空位的缓存池（16-Way Set）。而如果我们在程序中又使用了所谓优化神器的“内存对齐”的时候，这种争抢就会越发增多。效率上的损失也会变得非常明显。具体的实际测试我们可以参考： How Misaligning Data Can Increase Performance 12x by Reducing Cache Misses 一文。
这里我们引用一张Gallery of Processor Cache Effects 中的测试结果图，来解释下内存对齐在极端情况下带来的性能损失。
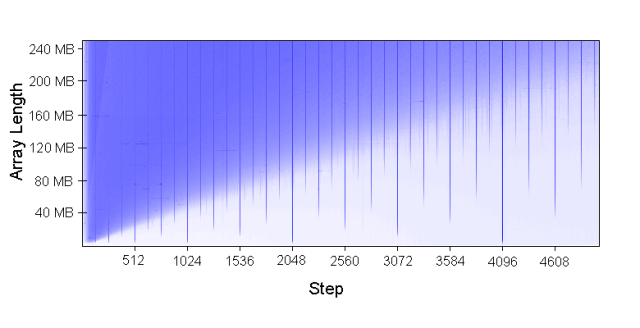
memory_align

该图实际上是我们上文中第一个测试的一个变种。纵轴表示了测试对象数组的大小。横轴表示了每次数组元素访问之间的index间隔。而图中的颜色表示了响应时间的长短，蓝色越明显的部分表示响应时间越长。从这个图我们可以得到很多结论。当然这里我们只对内存带来的性能损失感兴趣。有兴趣的读者也可以阅读原文分析理解其他从图中可以得到的结论。

从图中我们不难看出图中每1024个步进，即每1024*4即4096Bytes，都有一条特别明显的蓝色竖线。也就是说，只要我们按照4K的步进去访问内存(内存根据4K对齐），无论热点数据多大它的实际效率都是非常低的！按照我们上文的分析，如果4KB的内存对齐，那么一个80MB的数组就含有20480个可以被访问到的数组元素；而对于一个每512K就会有set冲突的16Way二级缓存，总共有512K/20480=25个元素要去争抢16个空位。那么缓存命中率只有64%，自然效率也就低了。

想要知道更多关于内存地址对齐在目前的这种CPU-Cache的架构下会出现的问题可以详细阅读以下两篇文章：

Cache淘汰策略

在文章的最后我们顺带提一下CPU Cache的淘汰策略。常见的淘汰策略主要有LRU和Random两种。通常意义下LRU对于Cache的命中率会比Random更好，所以CPU Cache的淘汰策略选择的是LRU。当然也有些实验显示在Cache Size较大的时候Random策略会有更高的命中率