格形变算法（Linear rotation-invariant coordinates和As-Rigid-As-Possible）

http://www.cnblogs.com/shushen/p/4977870.html

      在三维网格形变算法中，个人比较喜欢下面两个算法，算法的效果都比较不错， 不同的是文章[Lipman et al. 2005]算法对控制点平移不太敏感。下面分别介绍这两个算法：

　　文章[Lipman et al. 2005]提出的网格形变算法需要求解两次稀疏线性方程组：第一个方程定义了网格上离散坐标系之间的关系，通过求解该方程可以重组每个顶点的坐标系；第二个方程记录了顶点在局部坐标系的位置信息，通过求解该方程可以得到每个顶点的几何坐标。

在网格顶点建立局部坐标系（b₁ⁱ，b₂ⁱ，Nⁱ），i∈V。对于(i，j)∈E，定义差分算子δ：

δ_j(b₁ⁱ) = b₁^j – b₁ⁱ

δ_j(b₂ⁱ) = b₂^j – b₂ⁱ

δ_j(Nⁱ) = N^j – Nⁱ

       将差分算子表示为b₁ⁱ，b₂ⁱ，Nⁱ的形式：

δ_j(b₁ⁱ) = C₁₁^ijb₁ⁱ + C₁₂^ijb₂ⁱ + C₁₃^ijNⁱ

δ_j(b₂ⁱ) = C₂₁^ijb₁ⁱ + C₂₂^ijb₂ⁱ + C₂₃^ijNⁱ

δ_j(Nⁱ) = C₃₁^ijb₁ⁱ + C₃₂^ijb₂ⁱ + C₃₃^ijNⁱ

       进一步表示为：

b₁^j = (C₁₁^ij+1)b₁ⁱ + C₁₂^ijb₂ⁱ + C₁₃^ijNⁱ

b₂^j = C₂₁^ijb₁ⁱ + (C₂₂^ij+1)b₂ⁱ + C₂₃^ijNⁱ

N^j = C₃₁^ijb₁ⁱ + C₃₂^ijb₂ⁱ + (C₃₃^ij+1)Nⁱ

　　上式为第一个方程，记录了网格上离散坐标系之间的关系，其中的系数可以由原始网格得到。

x^j -xⁱ = <e_ij , b₁ⁱ >b₁ⁱ + <e_ij , b₂ⁱ >b₂ⁱ + <e_ij , Nⁱ >Nⁱ

　　上式为第二个方程，记录了顶点在局部坐标系的位置信息，其中的系数也可以由原始网格得到。

　　算法效果：

 

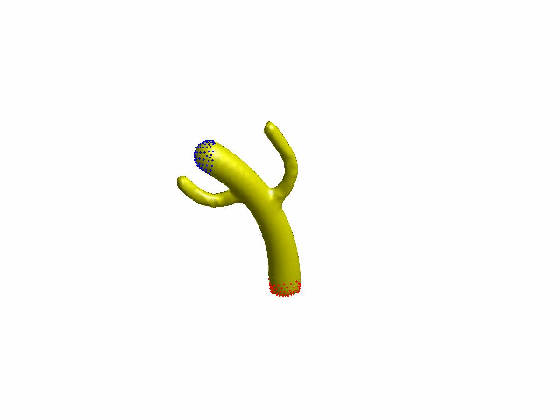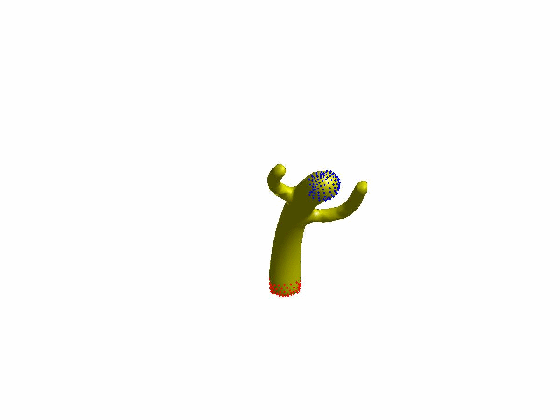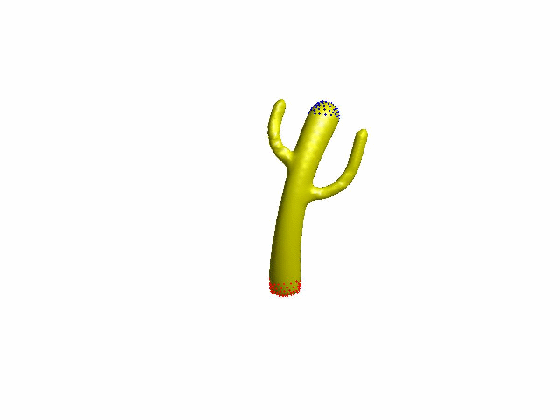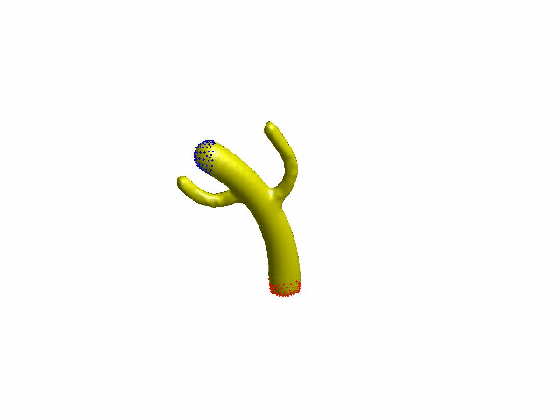
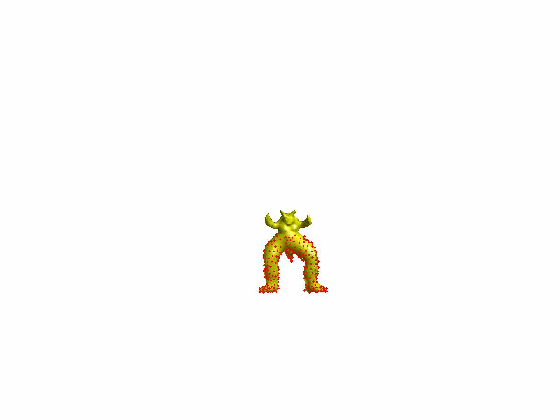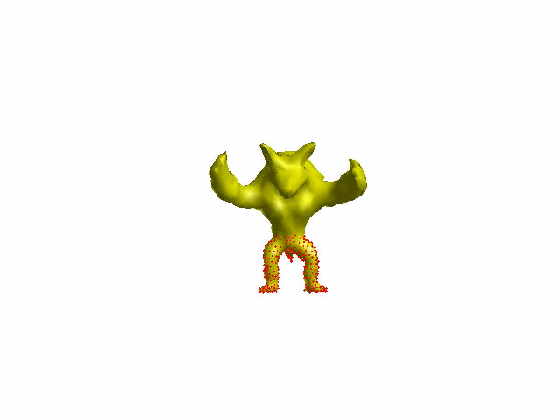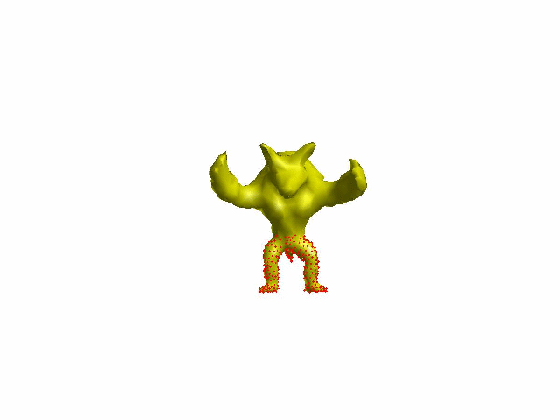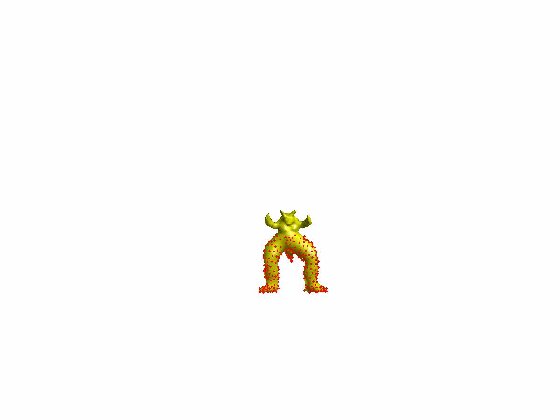
　　文章[Sorkine et al. 2007]提出了ARAP的网格形变算法，网格顶点的一环邻域三角片组成一个单元（Cell），当顶点i对应的单元C_i变形为C_i’时，定义其刚性（rigidity）能量函数为：

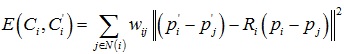
　　网格上所有单元的刚性能量之和为：

 

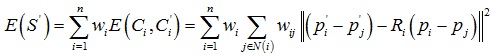
　　根据能量函数，算法实现过程分两步进行迭代，第一步更新R_i，第二步更新 p_i’，下面为具体推导过程。

　　1.更新R_i：

　　设e_ij = p_i - p_j，那么能量函数E(S’)可以表示为：

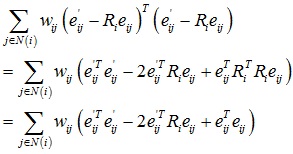
　　忽略不含R_i的项，那么：

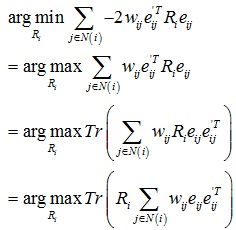
　　定义协方差矩阵S_i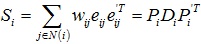：，将S_i奇异值分解：S_i = U_iΣ_iV_i^T，那么R_i = V_iU_i^T。

　　2.更新p_i’：

　　权重w_ij和w_i分别为：w_ij = 1/2(cotα_ij + cotβ_ij)，w_i = 1。我们将E(S’)对p_i’求偏导，并令其等于零：

 

　　上式中w_ij = w_ji，于是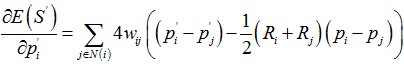，那么我们可以得到：

 

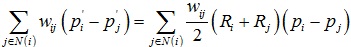
　　上式相当于求解稀疏矩阵方程组。

　　算法效果：

 

 

 

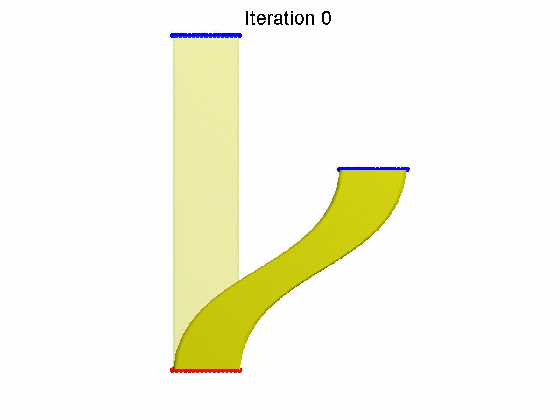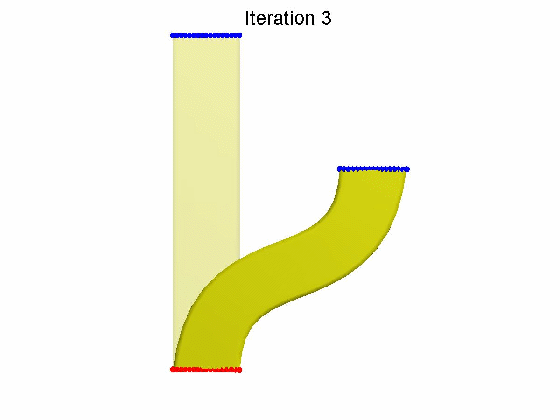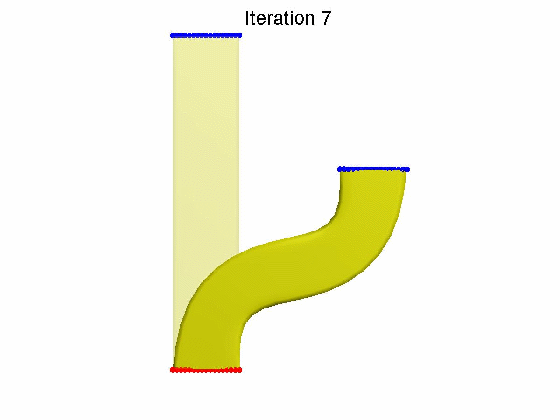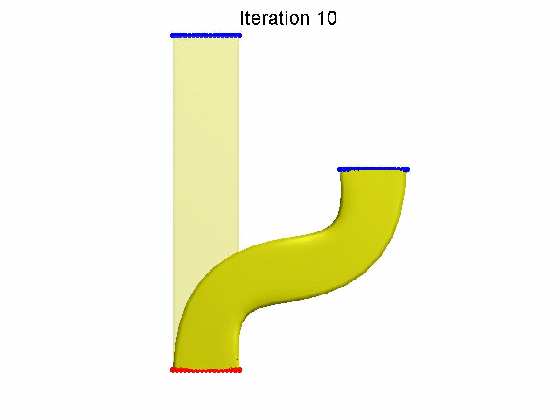
参考文献：

[1] Y. Lipman, O. Sorkine, D. Levin, and D. Cohen-Or. 2005. "Linear rotation-invariant coordinates for meshes." In ACM SIGGRAPH 2005 Papers (SIGGRAPH '05) 24:3 (2005), 479-487.

[2] O. Sorkine and M. Alexa. "As-Rigid-As-Possible Surface Modeling." In Proc. of Eurographics Symposium on Geometry Processing. Aire-la-Ville, Switzerland: Eurographics Association, 2007.