最小二乘法构建线性回归方程

一、线性回归的意义

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。由于市场现象一般是受多种因素的影响，而并不是仅仅受一个因素的影响。所以应用一元线性回归分析预测法，必须对影响市场现象的多种因素做全面分析。只有当诸多的影响因素中，确实存在一个对因变量影响作用明显高于其他因素的变量，才能将它作为自变量，应用一元相关回归分析市场预测法进行预测。
一元线性回归分析法的预测模型如下：

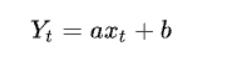
式中，x_t代表t期自变量的值；
Y_t代表t期因变量的值；
a、b代表一元线性回归方程的参数。
a、b参数由下列公式求得：

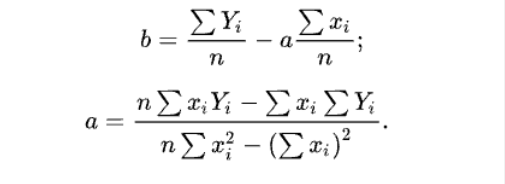
相关系数R²是用以反映变量之间相关关系密切程度的统计指标。我们可以用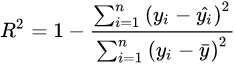
来刻画回归的效果。对于已经获取的样本数据，R²表达式中的总体平方和

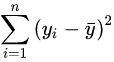
为确定的数。因此R²越大，意味着残差平方和

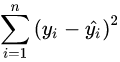
越小，即模型的拟合效果越好；R²越小，残差平方和越大，即模型的拟合效果越差。在线性回归模型中，R²表示解释变量对于预报变量变化的贡献率。R²越接近于1，表示回归的效果越好。

二、线性回归的使用

使用工具：Excel，jupyter，身高体重数据集 提取码：f9bz

1.在Excel中练习线性回归

用excel打开下载的身高体重数据集，在weights_heights中选择前二十组数据，在选中的二十组数据右下角弹出的快速分析中选择散点图：

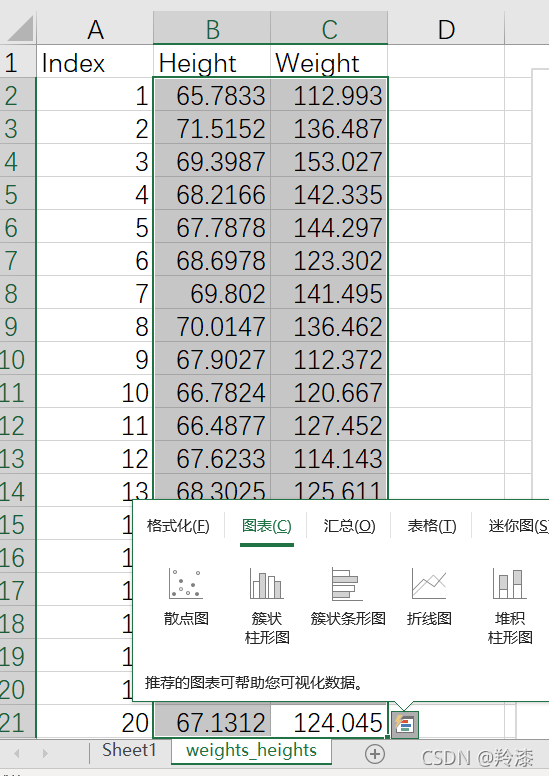
excel会自动根据选择的数据生成对应的散点图，再根据如下方法打开趋势线中的更多选项，勾选显示公式和显示R平方值：

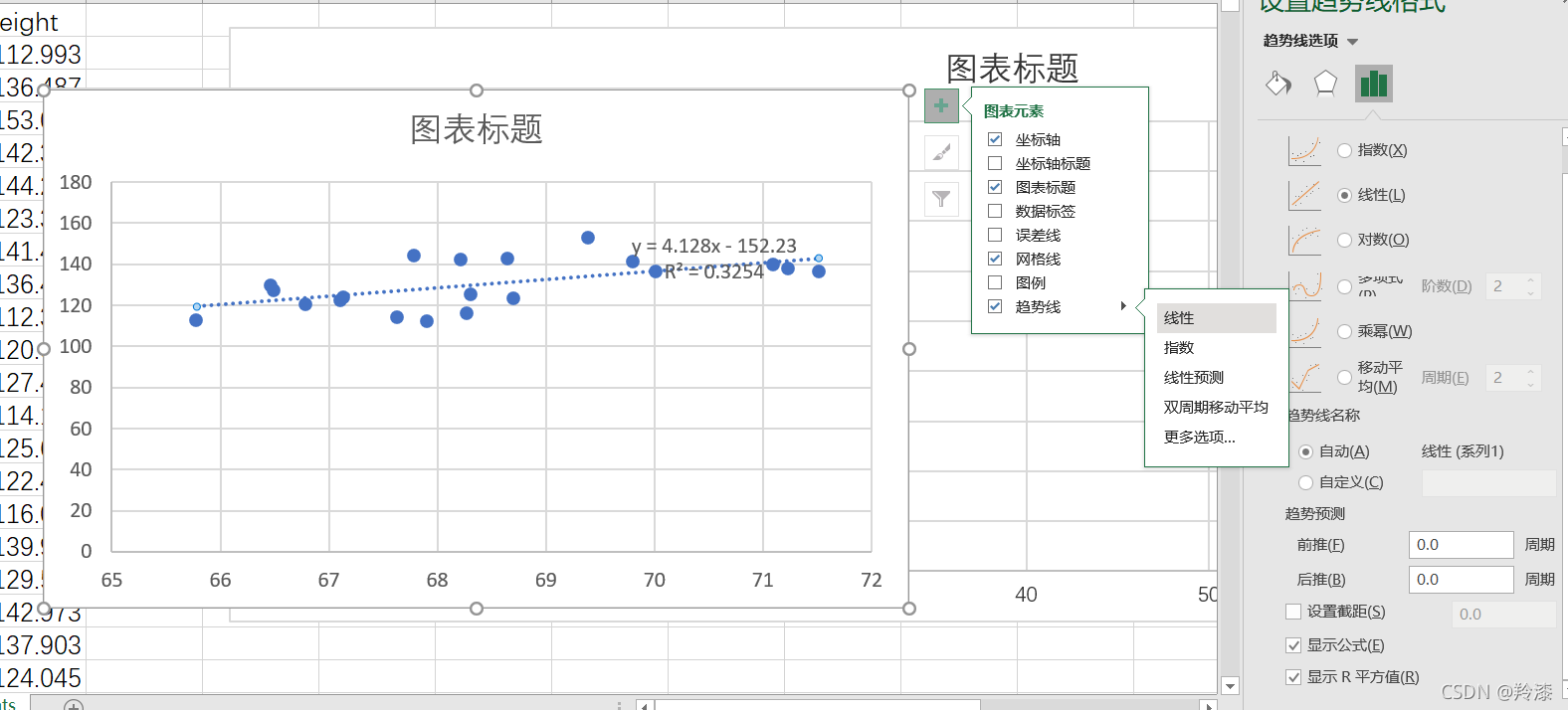
可以看到，excel自动生成了二十组数据的散点图并求出了线性回归公式和对应的相关系数。如法炮制，我们选择200组，2000组，20000组数据分别构造线性回归：

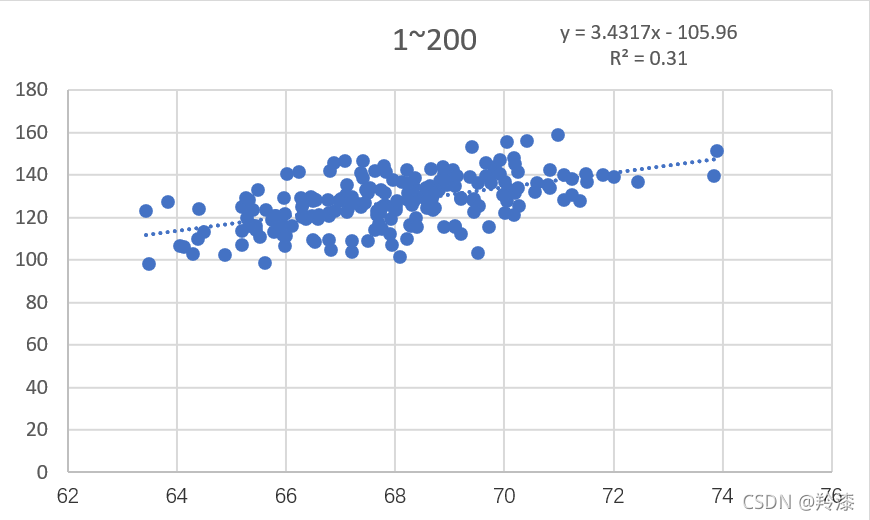
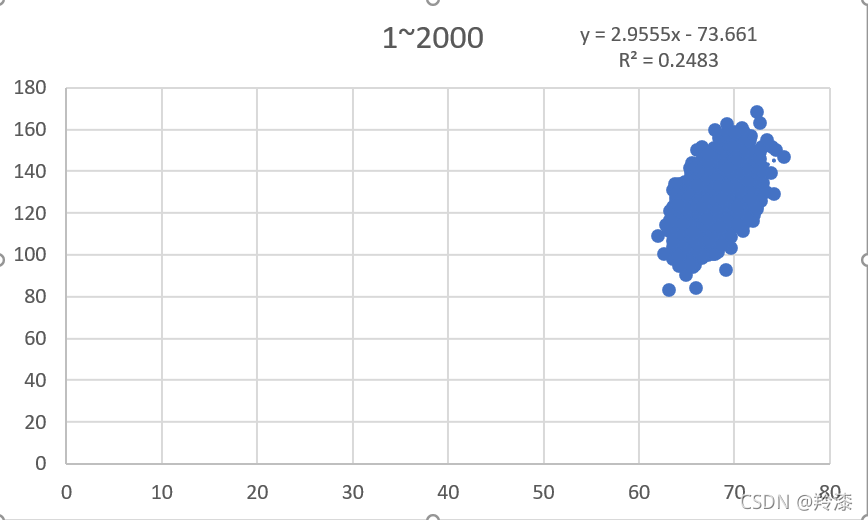
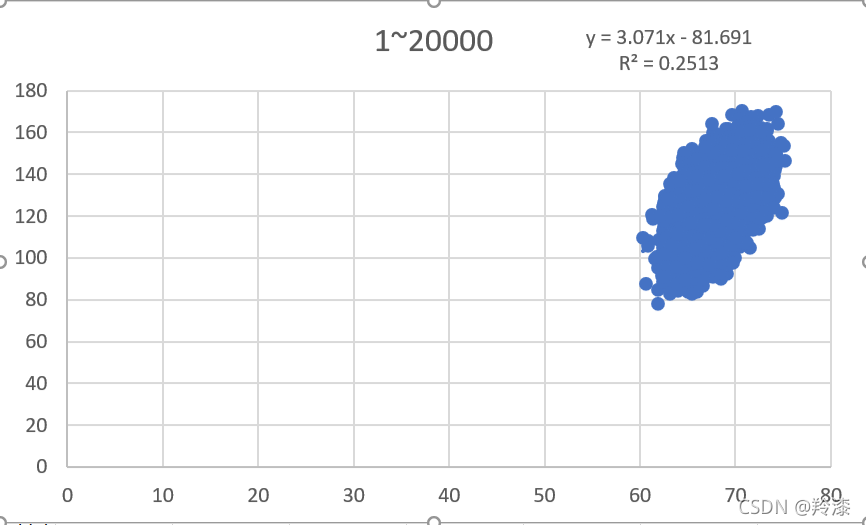
以上结果显示，并不是使用越多数据构建的线性回归方程就越准确，选择的数量与线性回归方程的拟合程度没有太大关系。那么同样数量的数据组，选择的数据不同对结果有不有影响呢，答案是有的，任意选择除前二十组外的二十组数据，构造线性回归方程，结果与前二十组的结果不同

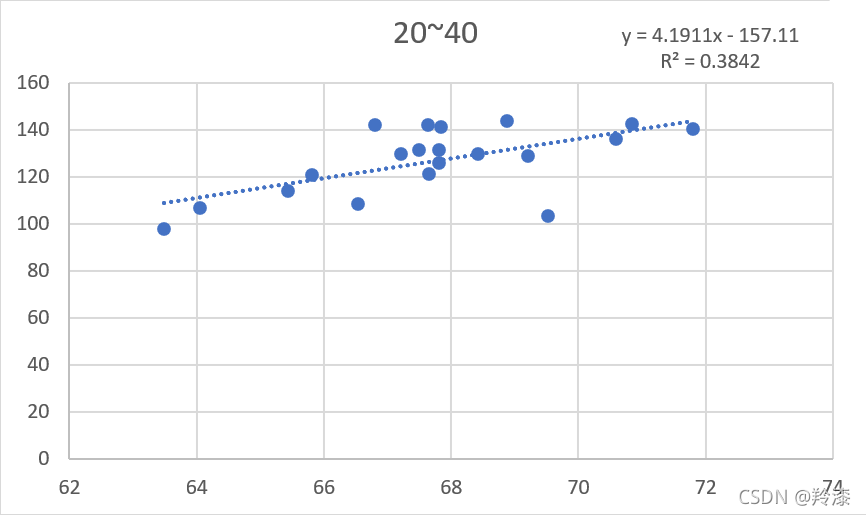
所以，在构造线性回归方程时，适当的选取数据能得到更好的结果。

2.使用jupyter来做一元线性回归分析

• 不调包实现一元线性回归

import pandas as pd
def read_file(raw):#根据行数来读取文件
    df = pd.read_excel('.\\weights_heights(身高-体重数据集).xls',sheet_name ='weights_heights')
    height=df.iloc[0:raw,1:2].values
    weight=df.iloc[0:raw,2:3].values
    return height,weight

def array_to_list(array):#将数组转化为列表
    array=array.tolist()
    for i in range(0,len(array)):
        array[i]=array[i][0]
    return array

def unary_linear_regression(x,y):#一元线性回归，x,y都是列表类型
    xi_multiply_yi=0
    xi_square=0;
    x_average=0;
    y_average=0;
    f=x
    for i in range(0,len(x)):
        xi_multiply_yi+=x[i]*y[i]
        x_average+=x[i]
        y_average+=y[i]
        xi_square+=x[i]*x[i]
    x_average=x_average/len(x)
    y_average=y_average/len(x)
    b=(xi_multiply_yi-len(x)*x_average*y_average)/(xi_square-len(x)*x_average*x_average)
    a=y_average-b*x_average
    for i in range(0,len(x)):
        f[i]=b*x[i]+a
    R_square=get_coefficient_of_determination(f,y,y_average)
    print('R_square='+str(R_square)+'\n'+'a='+str(a)+'  b='+str(b))
    
def get_coefficient_of_determination(f,y,y_average):#传输计算出的值f和x,y的真实值还有平均值y_average，获取决定系数，也就是R²
    res=0
    tot=0
    for i in range(0,len(y)):
        res+=(y[i]-f[i])*(y[i]-f[i])
        tot+=(y[i]-y_average)*(y[i]-y_average)
    R_square=1-res/tot 
    return R_square

raw=[20,200,2000,20000]
for i in raw:
    print('数据组数为'+str(i)+":")
    height,weight=read_file(i)
    height=array_to_list(height)
    weight=array_to_list(weight)
    unary_linear_regression(height,weight)

文件路径根据自己下载《身高体重数据集》的路径修改，点击运行：

• 调包实现一元线性回归

from sklearn import linear_model
from sklearn.metrics import r2_score
import numpy as np
import pandas as pd
def read_file(raw):#根据行数来读取文件
    df = pd.read_excel('.\\weights_heights(身高-体重数据集).xls',sheet_name ='weights_heights')
    height=df.iloc[0:raw,1:2].values
    weight=df.iloc[0:raw,2:3].values
    return height,weight

raw=[20,200,2000,20000]#要读取的行数
for i in raw:
    print('数据组数为'+str(i)+":")
    height,weight=read_file(i)
    weight_predict=weight
    lm = linear_model.LinearRegression()
    lm.fit(height,weight)
    b=lm.coef_
    a=lm.intercept_
    weight_predict=lm.predict(height)#计算有方程推测出来的值
    R_square=r2_score(weight,weight_predict)#计算方差
    print('b='+str(b[0][0])+' a='+str(a[0]))
    print('R_square='+str(R_square))

运行：

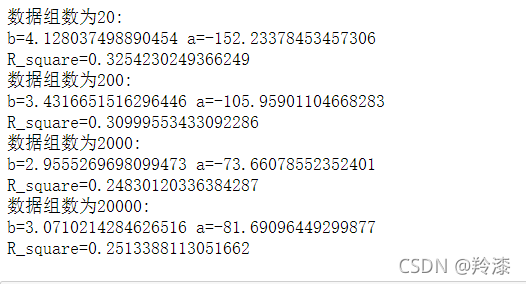
参考博客：最小二乘法构建线性回归方程