Physically Based Modeling: Particle System Dynamics(粒子运动)

最新推荐文章于 2024-11-05 11:31:32 发布

张赐

最新推荐文章于 2024-11-05 11:31:32 发布

阅读量3.6k

点赞数

本文链接：https://blog.csdn.net/zhangci226/article/details/3458981

版权

计算机动画专栏收录该内容

5 篇文章 1 订阅

订阅专栏

Physically Based Modeling: Particle System Dynamics

2008-11-23

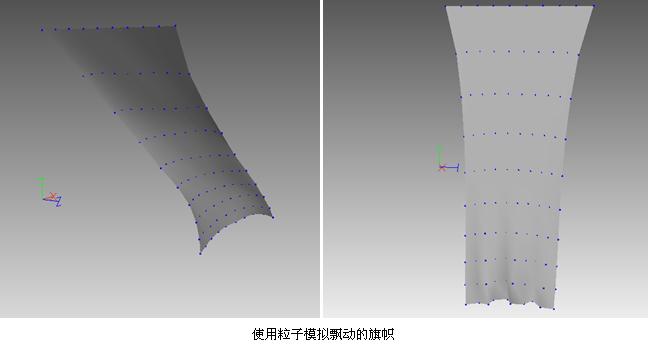
我们身边的所有物体几乎都是由粒子(Particle)所构成的。在计算机动画中，模拟真实的世界时候，不可避免的要模拟这些粒子的运动。比如胶状体果冻就是很典型的例子。在PSP上有一款叫做《LocoRoco》游戏，游戏的主角就是一个像果冻一样的东西，当它被其他物体挤压的时候，能够明显看到它的物理变形，模拟得相当真实。粒子运动不同于刚体运动，粒子运动时，可能会引起物体形状的变化，就像上面说的果冻一样。

一个粒子可以用它的位置和速度来描述。在描述粒子的时候，它的速度是一个瞬时速度，我们可以用一个向量来表示这个速度。这个速度是由时间t和位置来决定的，因为粒子在不动的时间和位置速度都不相等。我们可以用下面这个微分方程来描述它们之间的关系。

$/dot{X} = f(x,t)$

这里X(t)表示粒子P在不同时刻的位置，f(x,t)表示粒子P不同时刻，不同位置的速度。

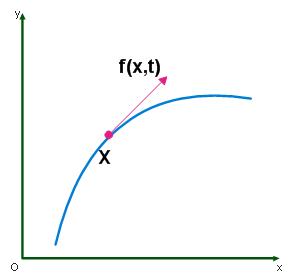
在上图中表示了一个粒子在某时刻的状态。其实这是一个初始值的问题，如果把粒子在不同的时刻放到不同的地方，那么它的速度是不一样。即使在不同时刻放在同一地方，粒子的速度也是不一样的。粒子是沿着途中蓝色的这条轨迹运动的，在很短的时间内( )，我们可以把粒子的运动轨迹看成是直线的，于是可以通过这种方法来近似模拟粒子的运动。下面用欧拉(Euler)方法来近似。在欧拉方法中，给出下面的等式。

$X(t+/Delta t) = X(t)+ /Delta t /cdot f(x,t)$

这是一种用线性函数替代非线性函数的方法。从上式中可以看到其实这是泰勒(Taylor)的展开式的切断，因为这个式子可以写成

$X(t+/Delta t) = X(t) + /dot{X} /cdot /Delta t$

而泰勒展开式：

$f(x)= f(x_{0})+ f'(x_{0})(x-x_{0})+ /frac{f''(x_{0})}{2!}(x-x_{0})^{2}+......+ /frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}$

前面已经说过了 $/dot{X} = f(x,t)$ 。但是用欧拉方法很不精确，且不稳定，从公式中我们可以看到它对于二阶导数以后的高阶导数等于0的函数可以准确的近似。在欧拉方法中，近似的精确程度取决于时间间隔长短 $/Delta t$ 。越小 $/Delta t$ ，近似得越精确。

　　上图中可以看到，蓝色是粒子实际运动轨迹，红色的是使用较小 $/Delta t$ 来近似的轨迹，黄色的使用较大的 $/Delta t$ 来近似的轨迹。当然还有很多方法来近似粒子的运动，这里只用欧拉方法来模拟粒子的运动。

下面来看看怎样具体的描述粒子的状态。

我们可以在“相空间”里描述粒子的状态，“相空间”是一个六维空间，我们可以分别

用位置和速度来描述： $/begin{bmatrix} X// V /end{bmatrix}$ ，和它的导数来描述 $/begin{bmatrix} /dot{X}// /dot{V} /end{bmatrix}$ ，于是可以得到： $/begin{bmatrix} /dot{X}// /dot{V} /end{bmatrix} = /begin{bmatrix} v// /frac{f}{m} /end{bmatrix}$

因为对速度在求导数可以得到它的加速度，再根据F = ma可以得到上面的结果。于是一个粒子可以描述为：

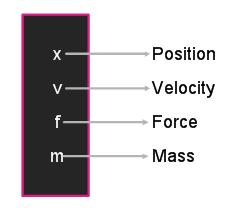
一个粒子系统由很多粒子所组成，我们可以用下面的图来表示。

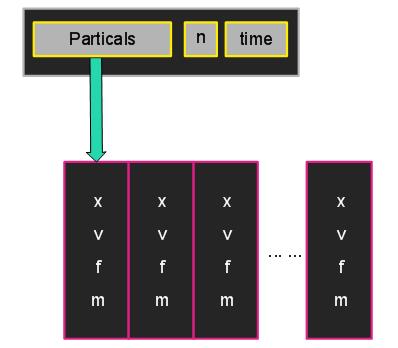
当然力也存在在粒子系统中，现在我们把力也添加到粒子系统中。

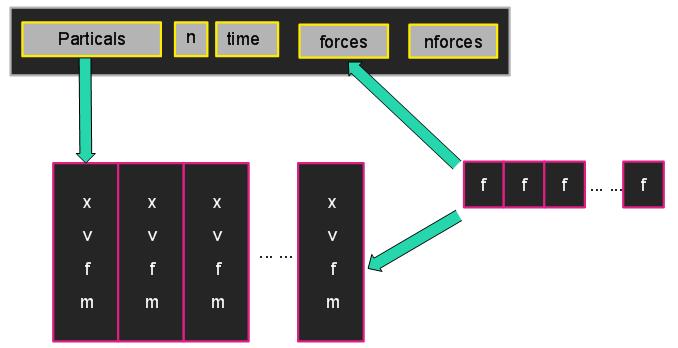
下面来看看一个系统都有可能受到那些力的影响。

重力(Gravity)

万物都受到重力的影响，根据公式可以很容易计算出重力的大小，当然它的方向是向下的。

$f_{grav}=mg$

在系统中，重力和粒子，粒子系统间的关系可以用下图来表示。

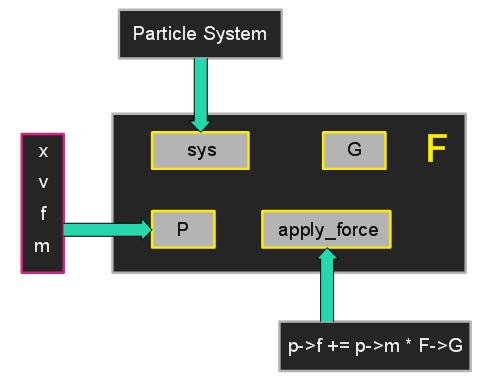
从图中可以看出粒子，粒子系统，力之间的关系。一个力包含了很多信息，其中sys表示这个力属于哪个粒子系统，p表示这个力作用于哪些粒子，G表示重力常数，apply_force是计算该力的方法。

粘滞拽力(Viscous Drag)

粘滞拽力是粒子间相互作用的力。它的公式是：

$f_{drag}=-kv$

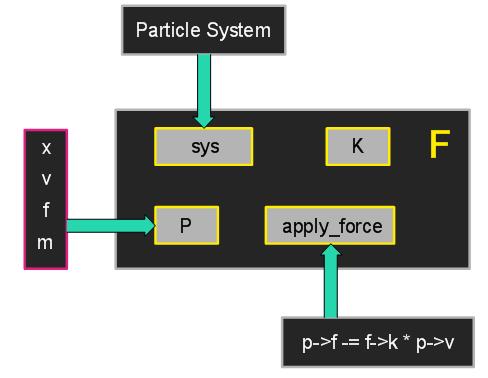
整个模型和重力是一样的，只是重力常数G变成了粘滞拽力常数K。

阻尼弹力(Damped Spring)

阻尼弹力也是粒子间相互作用的力，它的计算有个比较复杂的公式，如下。

$f_{1}= -/left[ k_{s}(|/Delta x-r|)+ k_{d}/left(/frac{/Delta v /cdot /Delta x }{|/Delta x|}/right) /right] /frac{/Delta x}{|/Delta x|}$

这里 $k_{S}$ 和 $k_{d}$ 都是阻尼常数。 $/Delta x$ 是弹簧被拉伸或压缩后的距离，在这里就是2个粒子间的实际距离，r是弹簧自然长度， $/Delta v$ 是弹簧两端粒子的速度差，下面这个图描述了它们的关系。

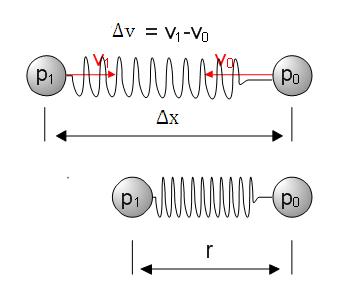
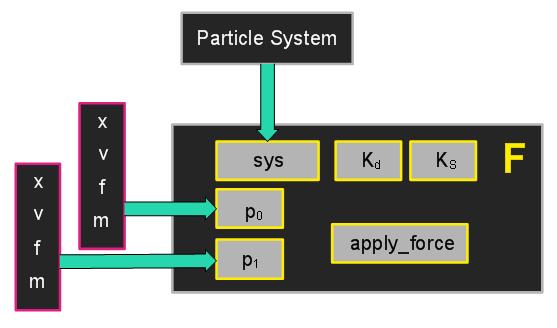
同样它和粒子，粒子系统间有下面的关系。

下面用代码实现一个粒子系统的主要部份。

 
 // 
//关于力的基类，将它定义为虚类是因为可以很方便的继承和修改里面的函数。 
// 
class GForceObj
{
public:
    GForceObj() {};
    virtual ~GForceObj() {};
    
    virtual void SetGravity(const GVector3 &_Force) {};  
    virtual void SetForce(const GVector3 &_Force) {}; 
    virtual void ApplyForce() = 0;
    
    //友元类 
    friend class GParticle;
    friend class GPSystem;
};
// 
//派生于力基类的重力 
// 
class Gravity : public GForceObj
{
public:
    Gravity(const GVector3 &_Force = GVector3(0.0, -9.8, 0.0));
    Gravity(const Gravity ©);
    virtual ~Gravity() {};
    void AddParticle(GParticle *P);
    virtual void SetGravity(const GVector3 &_Force);
    virtual void ApplyForce();
    friend class GParticle;
    friend class GPSystem;
private:
    GVector3 Force;
    vector<GParticle *> Particles;
};
// 
//粘滞拽力 
// 
class GViscosity : public GForceObj
{
public:
    GViscosity(const double &_Kd = 1.0);
    GViscosity(const GViscosity ©);
    virtual ~GViscosity() {};
    void AddParticle(GParticle *P);
    virtual void ApplyForce();
private:
    double Kd; //粘滞常数 
    vector<GParticle *> Particles;
};
// 
//外力，粒子除了收到重力，粘滞拽力，弹力的影响外，还可以受到外力的影响 
// 
class GExtForce: public GForceObj
{
public:
    GExtForce(const GVector3 &_Force = GVector3());
    GExtForce(const GExtForce ©);
    virtual ~GExtForce() {};
    void AddParticle(GParticle *P);
    virtual void SetForce(const GVector3 &_Force);
    virtual void ApplyForce();
private:
    GVector3 Force;
    vector<GParticle *> Particles;
};
// 
// 关于描述弹力信息的类，一个弹力连接了2个粒子，相当于一个弹簧连接了2个粒子 
// 在粒子系统中，我们要通过这个类来设定弹簧的自然长度，和连接的粒子 
// 
class GSpringInfo
{
public:
    GSpringInfo(){};
    GSpringInfo(GParticle* _P0,GParticle* _P1,double _len);
    
private:
    double InitLen; //弹簧自然长度 
    GParticle *P0; //粒子1 
    GParticle *P1; //粒子2 
    friend class GSpring;
};
// 
//弹力 
// 
class GSpring : public GForceObj
{
public:
    GSpring(const double &_Ks, const double &_Kd);
    GSpring(const GSpring ©);
    virtual ~GSpring(){};
    void AddSpringInfo(GSpringInfo* sif);
    virtual void ApplyForce();
private:
    float Ks,Kd; //阻尼系数 
    vector<GSpringInfo *> SpringInfo;
};
//粒子类 
class GParticle
{
public:
    //初始化粒子，默认质量为1.0 
    GParticle(const double &_Mass = 1.0, const GVector3 &_Pos = GVector3(), const GVector3 &_Vel = GVector3(), const GVector3 &_Force = GVector3(),bool movable = true);
    GParticle(const GParticle ©);
    ~GParticle();
    void SetPos(const double &x, const double &y, const double &z); //设置粒子的位置 
    void SetMovable(bool movable); //设置该粒子是否可以移动 
    GVector3 GetPos() const;
    friend class GPSystem;
    friend class GForceObj;
    friend class GExtForce;
    friend class Gravity;
    friend class GViscosity;
    friend class GSpring;
private:
    double Mass; //质量 
    GVector3 Pos; //位置 
    GVector3 Vel; //速度 
    GVector3 Force; //力 
    bool Movable; //是否可以移动 
};
// 
//粒子系统 
// 
class GPSystem
{
public:
    GPSystem();
    GPSystem(const GPSystem ©);
    ~GPSystem();
    
    void ClearForce(); //清空所有的力(设置所有力为0) 
    void ComputeForce(); //计算力 
    void EulerStep(const double &dt); //这就是上面说的是用欧拉方法来模拟粒子运动 
    void AddParticle(GParticle *P);// 添加粒子到粒子系统 
    void AddForce(GForceObj *F); //添加力到粒子系统 
    int GetNumParticle() const; //获取粒子总个数 
    int GetNumForce() const; //获取力的总个数 
    GParticle *GetParticle(int idx); //获取粒子 
    GForceObj *GetForce(int idx); //获取力 
    friend class GForceObj;
    friend class Gravity;
    friend class GViscosity;
    friend class GExtForce;
    
private:
    double Time; //欧拉方法中的时间步长，越小模拟越精确 
    GParticle* pParticle;
    vector<GParticle *> Particles;
    vector<GForceObj *> Forces;
};
GPSystem::~GPSystem()
{
    //删除所有粒子 
    vector<GParticle *>::iterator it0;
    for (it0 = Particles.begin(); it0 != Particles.end(); ++it0)
        delete (*it0);
    
    //删除所有力 
    vector<GForceObj *>::iterator it1;
    for (it1 = Forces.begin(); it1 != Forces.end(); ++it1)
        delete (*it1);
}
void GPSystem::ClearForce()
{
    int NumPtcle = (int)Particles.size();
    for (int i = 0; i != NumPtcle; ++i)
        Particles[i]->Force.Set(0.0, 0.0, 0.0);
}
void GPSystem::ComputeForce()
{
    int NumForce = (int)Forces.size();
    for (int i = 0; i != NumForce; ++i)
        Forces[i]->ApplyForce();
}
// 
//欧拉方法的实现 
// 
void GPSystem::EulerStep(const double &dt)
{
    int NumPtcle = (int)Particles.size();
    for (int i = 0; i != NumPtcle; ++i)
    {
        GVector3 xDot = Particles[i]->Vel; //xDot表示对位置求导数，得到了粒子的速度。 
        GVector3 vDot = Particles[i]->Force / Particles[i]->Mass;// vDot表示对速度求导数，得到了粒子的加速度，加速度就是f/m 
        Particles[i]->Pos += dt * xDot; //dt时间后的位置 
        Particles[i]->Vel += dt * vDot; //dt时间后的速度 
    }
}
// 
//重力 
// 
void Gravity::ApplyForce()
{
    int len = (int)Particles.size();
    for (int i = 0; i < len; ++i)
    {
        GParticle *Ptc = Particles[i];
        if(Ptc->Movable)
            Ptc->Force = Ptc->Force + Force;
    }
}
// 
//粘滞拽力 
// 
void GViscosity::ApplyForce()
{
    int len = (int)Particles.size();
    for (int i = 0; i < len; ++i)
    {
        GParticle *Ptc = Particles[i];
        if(Ptc->Movable)
            Ptc->Force = Ptc->Force - Kd * Ptc->Vel;
    }
}
// 
//外力 
// 
void GExtForce::ApplyForce()
{
    int len = (int)Particles.size();
    for (int i = 0; i < len; ++i)
    {
        GParticle *Ptc = Particles[i];
        if(Ptc->Movable)
            Ptc->Force = Ptc->Force + Force;
    }
    Force.Set(0.0, 0.0, 0.0);
}
// 
//弹力 
// 
void GSpring::ApplyForce()
{
    int len = (int)SpringInfo.size();
    for(int i=0; i<len; ++i)
    {
        GParticle *p0 = SpringInfo[i]->P0;
        GParticle *p1 = SpringInfo[i]->P1;
        GVector3 f0, f1;
        GVector3 l = p0->Pos - p1->Pos;
        GVector3 ldot = p0->Vel - p1->Vel;
        f0 = -(Ks * (norm(l) - SpringInfo[i]->InitLen) + Kd * ldot * l / norm(l)) * l / norm(l);
        f1 = -f0;
        if(p0->Movable) 
            p0->Force =  p0->Force + f0;
        if(p1->Movable)
            p1->Force =  p1->Force + f1;
    }
}
 